如何分析数值积分算法的精度与误差

数值积分算法的精度受如下两个主要因素的影响：计算机舍入误差和截断误差。计算机舍入误差是由于执行计算的计算机精度有限而产生的，该误差很难减小，除非使用计算精度更高的计算机。科学计算时一般使用双精度字长。精确解和数值解之间的差别主要是由截断误差决定的，截断误差来自于Taylor级数展开或多项式逼近时产生的误差。

在数值积分算法中，最有效的是那些计算量最小而能产生最精确结果的算法。一般而言，越高阶的算法能产生越精确的结果，但需要的计算量也更大。因此，希望采用最大的时间步长以减少计算的频率。对时间步长大小有影响的因素有多个，其中一个因素是每一步计算中算法自身引入的误差。这个误差就是局部截断误差（LTE），它来自于Taylor级数展开或多项式逼近产生的误差，取决于所使用的数值积分算法。术语“局部”强调了该误差来自于每一步计算本身，而不是前面各步计算的残余全局误差。由数值积分算法单步产生的误差可表示为

ε_T≜x（t_n+1）-x_n+1 （5.64）式中，x（t_n+1）为t_n+1时刻的精确解，而x_n+1为其数值近似解。上述定义中假定了x（t_n）=x_n，以表示该误差是单步计算引入的。局部截断误差可以用图5.4进行说明。

为了推导局部截断误差的表达式，将x（t_n-i）在t_n+1处展开：

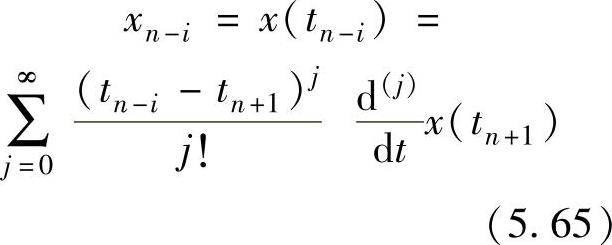
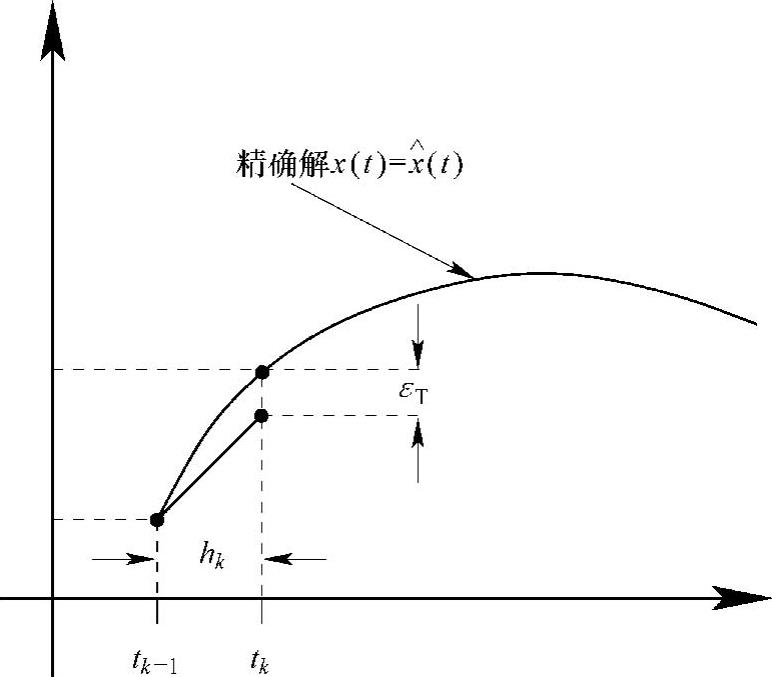
图5.4 局部截断误差的图形化描述

另有

求解x（t_n+1）-x_n+1可得

ε_T=C₀x（t_n）+C₁x（t_n-1）+C₂x（t_n-2）+…+Ckx（t_n-k）+C_k+1x（t_n-k-1）+… （5.67）

若算法的阶数为k，则前面的k个系数为零，故局部截断误差可表示为

ε_T=C_k+1h^k+1x^（k+1）（t_n+1）+O（h^k+2） （5.68）

式中，O（h^k+2）表示与h^k+2等阶的误差。

例5.5 推导向前Euler法、后退Euler法和梯形法的局部截断误差表达式。

解5.5

（1）向前Euler法

前面已讲述过向前Euler法的表达式为

x_n+1=x_n+hf（x_n，t_n）

由局部截断误差的定义有x_n=x（t_n），将其Taylor级数展开有

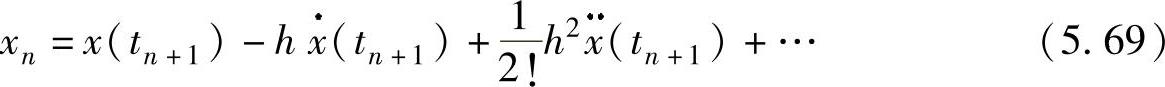
另外，

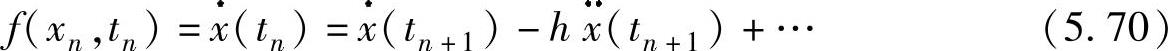
故有

（2）后退Euler法(www.xing528.com)

后退Euler法的表达式如下：

x_n+1=x_n+hf（x_n+1，t_n+1）

采用与向前Euler法相同的方法进行推导，但这里采用

可得

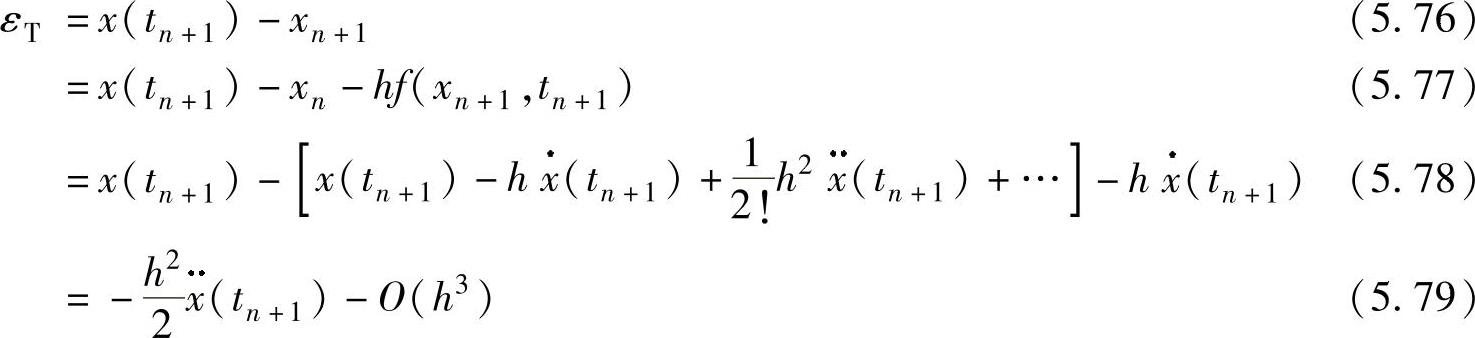
注意，向前Euler法和后退Euler法的局部截断误差是相等的，但符号不同；这个特性与例5.1的结果（见图5.2）是一致的，两种方法的误差相等只是符号相反。

（3）梯形法

二阶梯形法的表达式为

采用与前面相同的方法进行推导，有

两种一阶Euler法的局部截断误差都是h²阶的，但二阶梯形法的局部截断误差是h³阶的。梯形法和后退Euler法都是隐式法，每一步都需要迭代求解。考察梯形法的迭代求解式（5.49）：

同样地，后退Euler法的迭代式为

注意，这两种方法所需要的函数值估算量和计算量是相当的，但对于相同的时间步长h，梯形法的局部截断误差要比后退Euler法小得多。因此，相比后退Euler法，梯形法是一种使用更为广泛的通用隐式数值积分算法。

对于多步法，已推导出了局部截断误差的一般性表达式[6]。对于如下的一般性多步法计算公式：

其对于次数小于或等于k的多项式解是完全精确的；其局部截断误差可用下式表示：

ε_T=C_kx^（k+1）（τ）h^k+1=O（h^k+1） （5.88）

式中，-ph≤τ≤h，

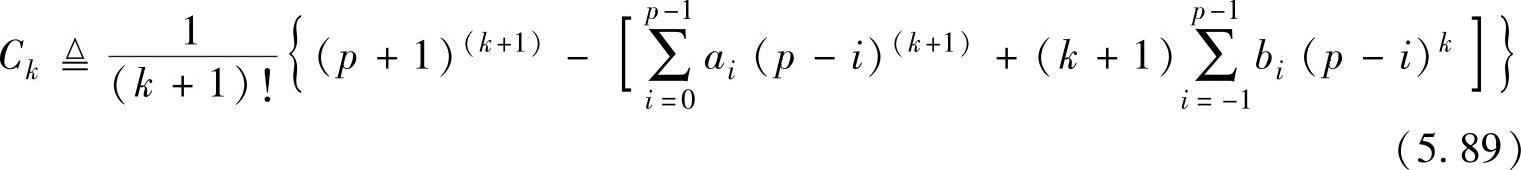
上述表达式提供了一个近似计算每一步局部截断误差（以x和h为变量的函数）的方法。