电力系统中的4.4应用探析

在电力系统应用中，经常会出现大型稀疏矩阵，包括状态估计、潮流计算、暂态和动态稳定性仿真等。这些应用的计算效率与问题本身的描述方式和稀疏矩阵求解技术的使用方式密切相关。为了更好地理解稀疏性对电力系统问题的影响，我们来考察如图4.20所示的IEEE 118母线系统的潮流Jacobi矩阵。

该系统的Jacobi矩阵具有1051个非零元，其结构如图4.21a所示。注意，非零元主要集中在主对角线和两个次对角线上，其中两个次对角线上的非零元是由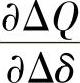 和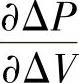产生的。对该Jacobi矩阵进行LU分解，分解后的结构如图4.21b所示，该矩阵有14849个非零元。注意，两个次对角线上的非零元产生了大量处于次对角线与主对角线之间的非零元注入。

图4.22a给出了根据方案0对节点重新排序后的潮流Jacobi矩阵结构。通过此种重新排序，次对角线上的非零元已不再存在。对此新的潮流Jacobi矩阵进行LU分解，分解后的矩阵结构如图4.22b所示。该矩阵只有1869个非零元，与没有排序的原始Jacobi矩阵相比，非零元注入减少了差不多一个数量级。

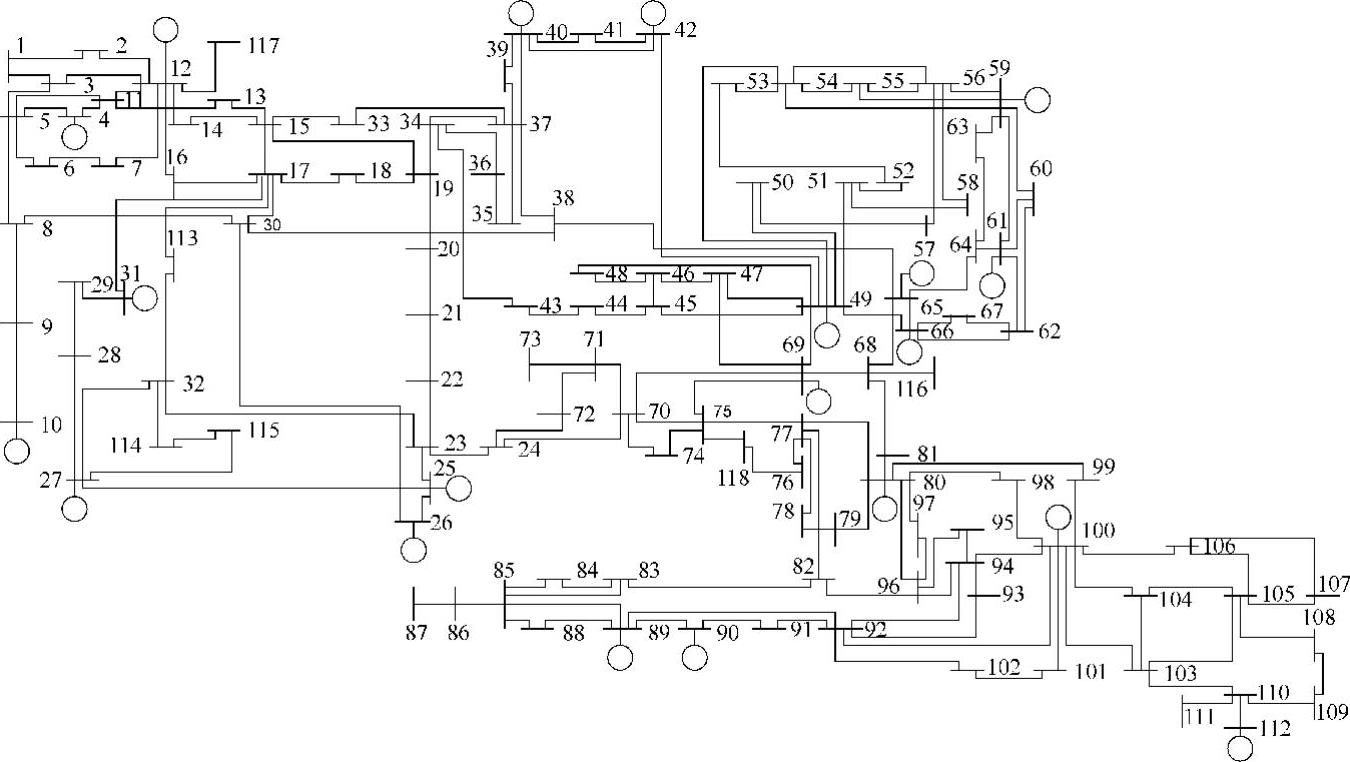
图4.20 IEEE 118母线系统

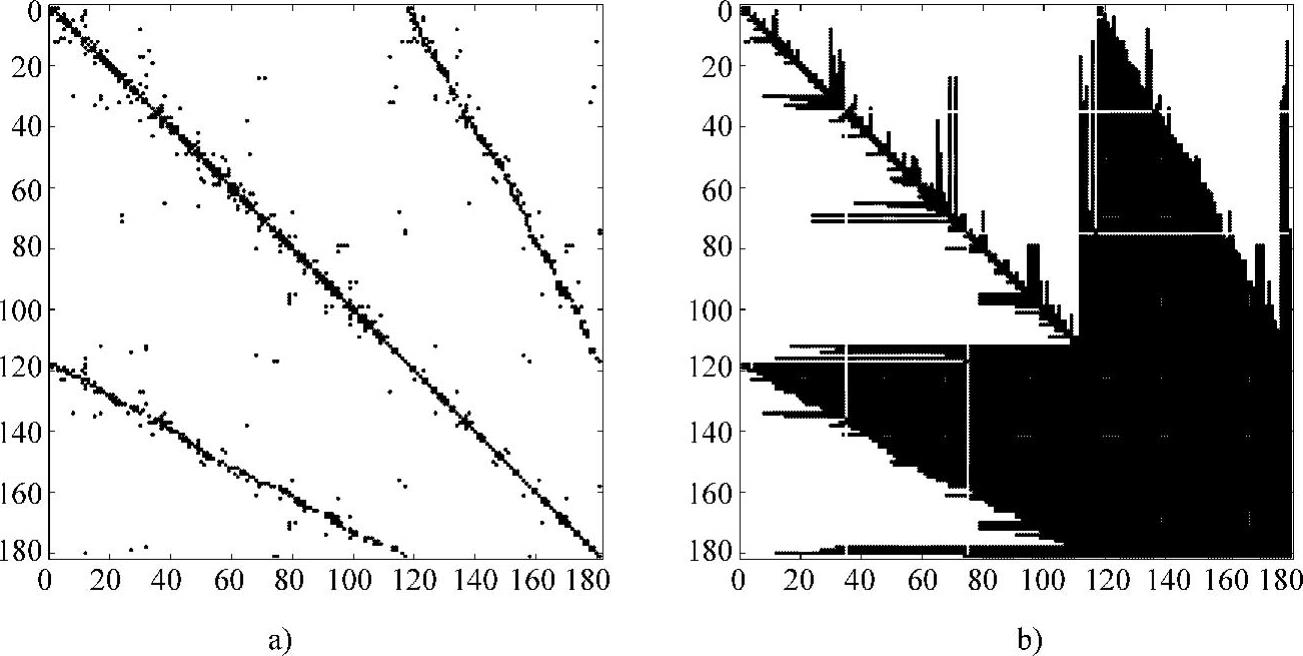
图4.21 IEEE 118母线系统

a）Jacobi行列式 b）LU分解的结果

图4.23a给出了根据方案Ⅰ对节点重新排序后的潮流Jacobi矩阵结构。注意，非零元是如何缓慢地向主对角线靠拢的，这会减少LU分解过程中的非零元注入数目。该矩阵LU分解的结构如图4.23b所示，具有1455个非零元。

最后，图4.24a给出了根据方案Ⅱ对节点重新排序后的潮流Jacobi矩阵结构，其LU分解后的矩阵结构如图4.24b所示。此排序方案只产生了1421个非零元，非零元注入减少了一个数量级以上。稀疏矩阵的LU分解时间近似为n²次乘法和除法。未进行节点排序的潮流计算每次迭代大致需要220.5×10⁶次乘法和除法，而按方案Ⅱ对节点进行重新排序后的潮流计算每次迭代只需要2.02×10⁶次乘法和除法。因此，节点重新排序后的系统其潮流计算比原始系统快100多倍！考虑将此求解时间乘以Newton-Raphson法潮流计算的迭代次数或时域积分中的时间步数后，不使用节点重新排序就直接进行计算显然是一种愚蠢的算法。(www.xing528.com)

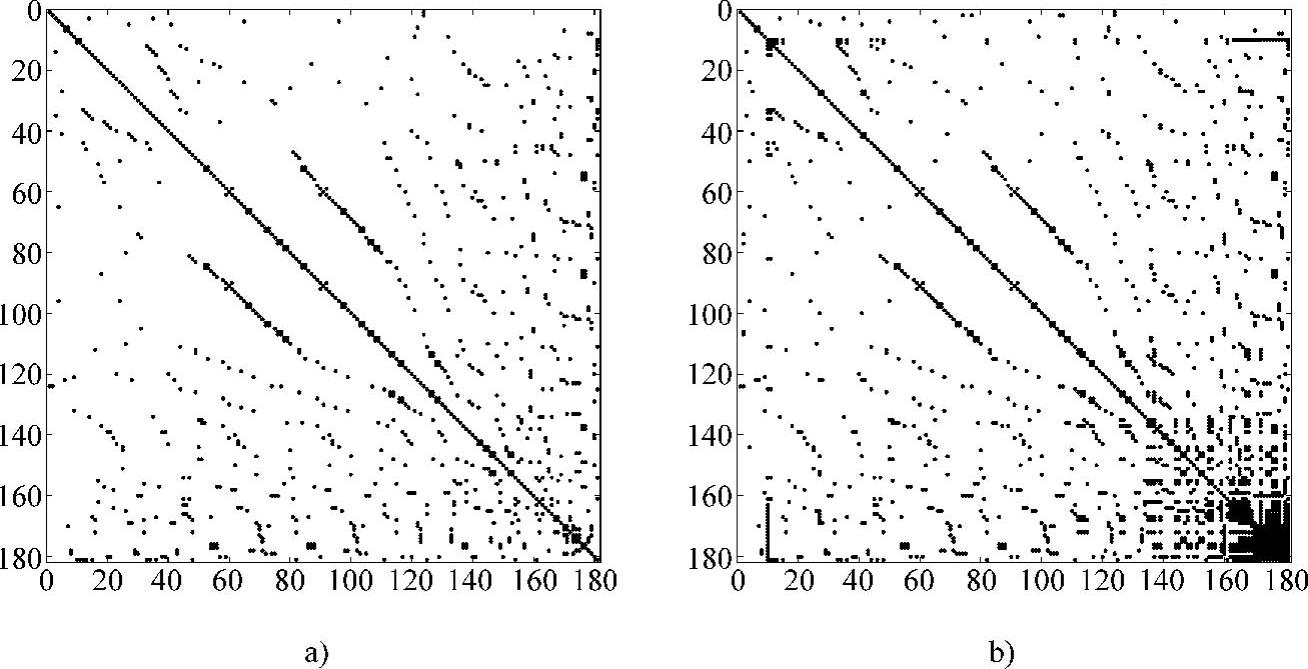
图4.22 IEEE 118母线系统方案0

a）Jacobi行列式 b）LU分解的结果

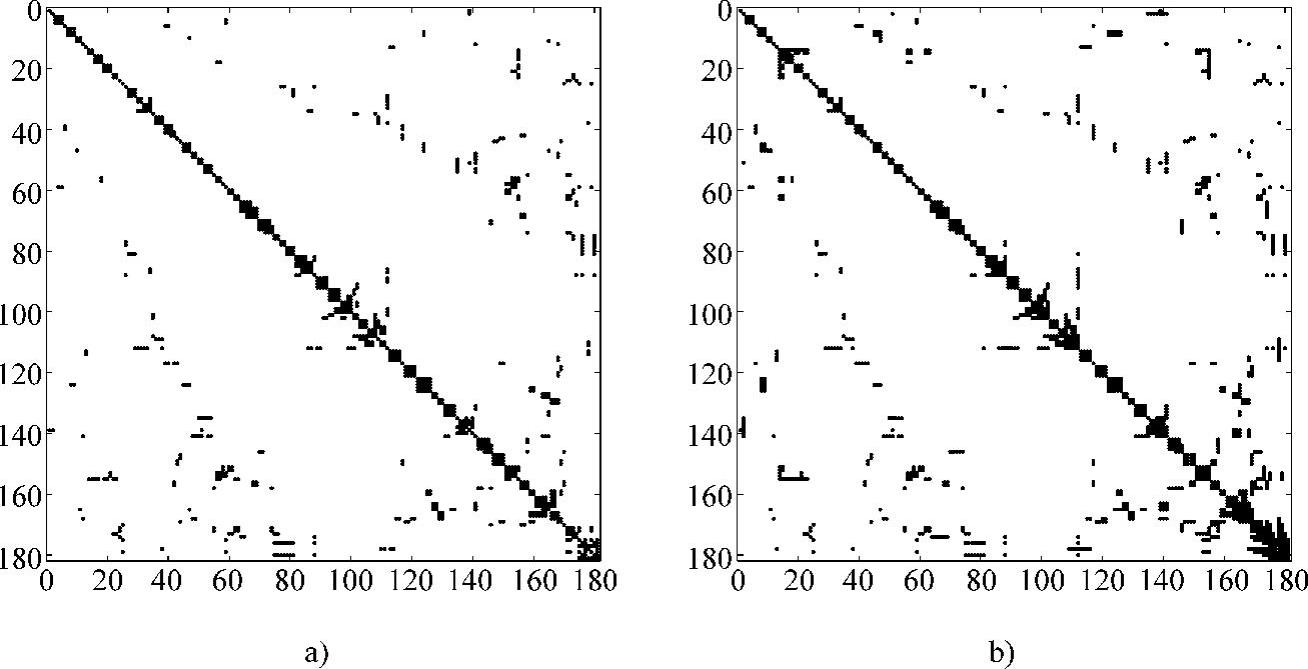
图4.23 IEEE 118母线系统方案Ⅰ

a）Jacobi行列式 b）LU分解的结果

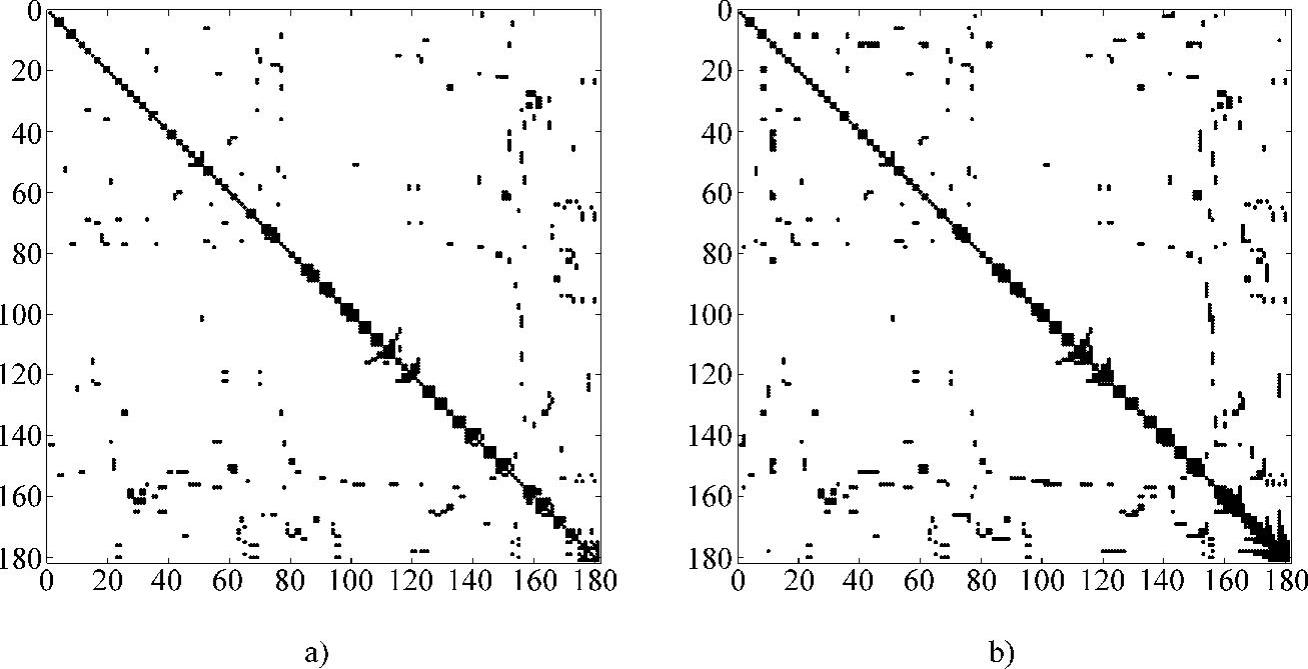
图4.24 IEEE 118母线系统方案Ⅱ

a）Jacobi行列式 b）LU分解的结果