减少非零元注入数的LU分解算法——Berry/Tinney II算法

方案0给出了一种节点排序的快速算法，该算法只对矩阵进行一次快速浏览，除了计算矩阵每个节点的度之外不需要其他计算，所得到的结果大致合理。方案Ⅰ在方案0的基础上进行了改进，它仍然基于最小度算法，但它对LU分解过程进行了模拟，在LU分解的每一步重新计算节点的度。对方案Ⅰ的进一步改进是开发一种算法，使LU分解的每一步的非零元注入数目最小化，这种算法本书称为方案Ⅱ。对于方案Ⅱ，在LU分解的每一步，需要考虑消去不同节点时所产生的非零元注入的数目。方案Ⅱ也被称作Berry算法或者TinneyⅡ算法。方案Ⅱ的计算步骤归纳如下：

方案Ⅱ

1.对每个节点，计算消去此节点后产生的非零元注入数目。

2.选择产生非零元注入最少的节点。

3.如果出现非零元注入数目相等的情况，选择度值最小的节点。

4.如果出现度值相等的情况，选择原节点号小的节点。

5.将选中的节点列入排序表中，然后消去该节点并相应地更新非零元注入和度的信息。

6.返回步骤1。

例4.9 利用方案Ⅱ重新排序例4.6中的矩阵。计算此排序下α、β的值以及非零元注入的数目。

解4.9 方案Ⅱ的排序算法考虑了当节点进入排序表并被消去后产生的非零元注入对整个排序过程的影响。原始矩阵各节点的度和相应的非零元注入信息如下所示：

从上表可以看出，消去节点6或9都不会产生额外的边，即非零元注入。因为出现了非零元注入数目相等的情况，因此具有最小度的节点被选中。这样，节点9被选中并消去。再次使用方案Ⅱ的算法，更新后的非零元注入数目和度的信息如下所示：(www.xing528.com)

下一个被消去的节点是节点6，因为它被消去时产生的非零元注入最少。消去节点6后，更新的非零元注入数目和度的信息如下所示：

可见，引入非零元注入最少的两个节点为节点4和节点8，但两个节点的度值相同，因此按照自然排序节点4被选中并消去。

继续使用方案Ⅱ的算法直到所有节点都被编号并消去，可以得到如下的排序结果。

排序Ⅱ=[9 6 4 8 2 1 3 5 7 10]

基于方案Ⅱ算法得到的排序结果重新对例4.6中的矩阵进行排序，所产生的非零元注入如图4.19所示。该排序仅产生10个非零元注入，使得α=84，β=54，从而α+β=138。这意味着计算量仅为原始未排序矩阵的68%。

方案Ⅰ致力于减少LU分解中的乘法和除法次数，而方案Ⅱ聚焦于减少前代/回代过程中的乘法和除法次数，而方案0则提供了简单快速的排序方法。方案Ⅰ在计算性能上的改进抵偿了其算法上的复杂度^[50]，而方案Ⅱ在计算性能上的改进常常无法抵偿其在实现上的复杂度。采用哪个方案更好视具体问题而定，最好是由使用者自己决定。

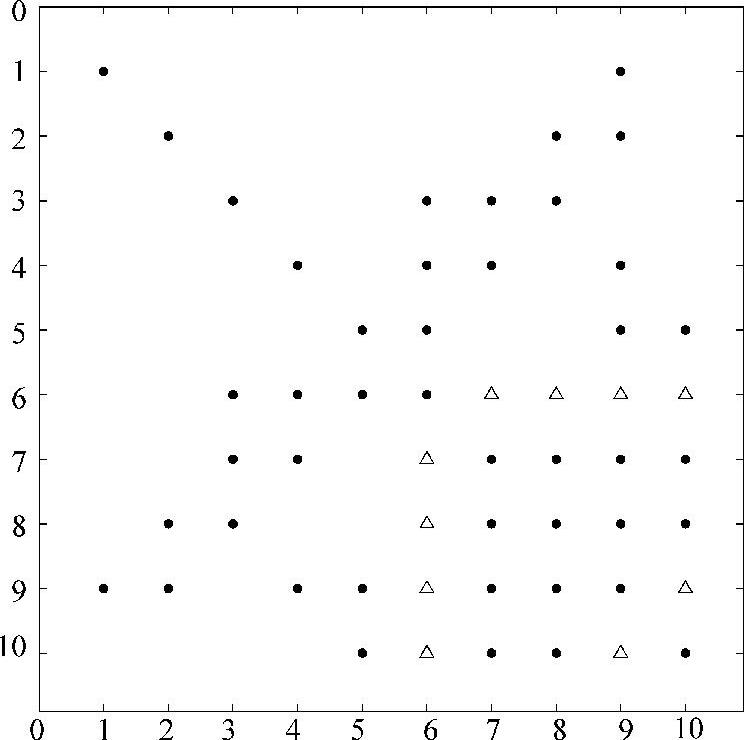
图4.19 加入非零元注入后例4.9的矩阵