优化节点排序方案以减少LU分解和前代/回代乘除法次数

节点排序方案对减少LU分解和前代/回代过程中的乘除法次数具有重要作用。一个好的排序方案在LU分解中产生的非零元注入会很少，非零元注入的定义是原始矩阵A中为零的元素在矩阵L或U中不再为零元素。如果A是一个满阵，那么LU分解过程需要的乘除法次数为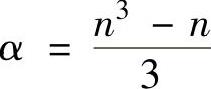 ，而前代/回代过程需要的乘除法次数为β=n²。如果采用合适的节点排序方案，求解稀疏矩阵所需要的乘除法次数可以大大减少。

例4.4 确定求解如图4.6所示系统所需的乘除法次数以及非零元注入数目。

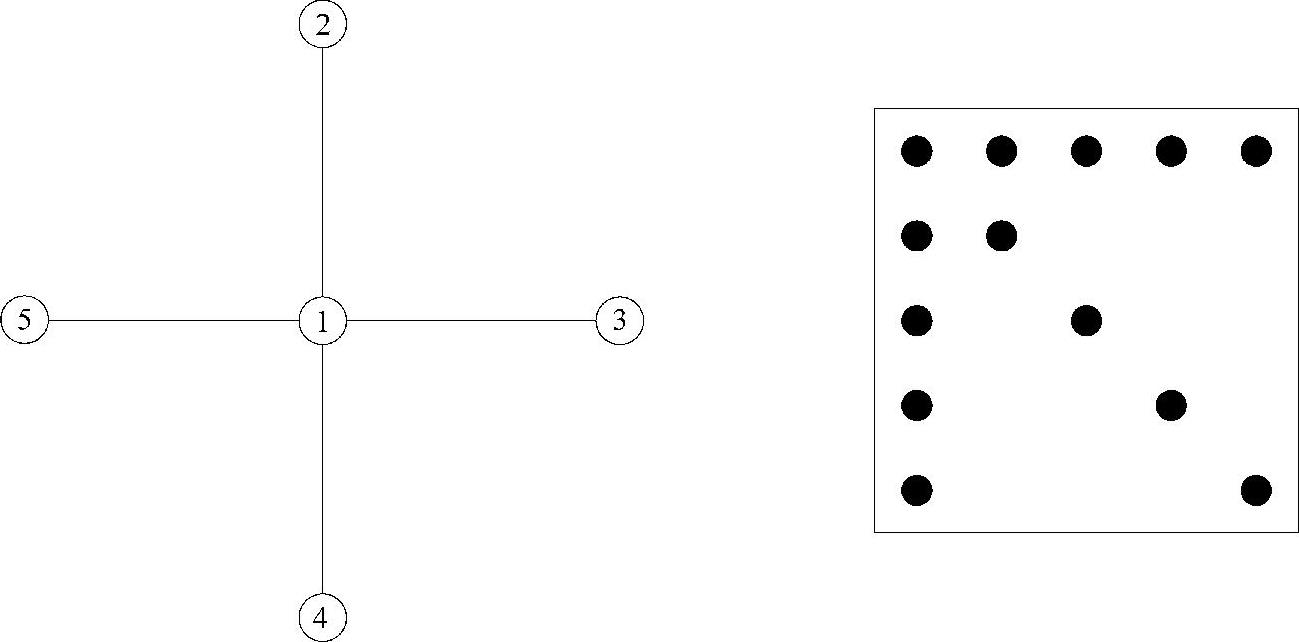
图4.6 例4.4的图与矩阵

解4.4 LU分解的步骤如下：

q₁₁=a₁₁

q₂₁=a₂₁

q₃₁=a₃₁

q₄₁=a₄₁

q₅₁=a₅₁

q₁₂=a₁₂/q₁₁

q₁₃=a₁₃/q₁₁

q₁₄=a₁₄/q₁₁

q₁₅=a₁₅/q11

q₂₂=a₂₂-q₂₁q₁₂

q₃₂=a₃₂-q₃₁q₁₂

q₄₂=a₄₂-q₄₁q₁₂

q₅₂=a₅₂-q₅₁q₁₂

q₂₃=（a₂₃-q₂₁q₁₃）/q₂₂

q₂₄=（a₂₄-q₂₁q₁₄）/q₂₂

q₂₅=（a₂₅-q₂₁q₁₅）/q₂₂

q₃₃=a₃₃-q₃₁q₁₃-q₃₂q₂₃

q₄₃=a₄₃-q₄₁q₁₃-q₄₂q₂₃

q₅₃=a₅₃-q₅₁q₁₃-q₅₂q₂₃

q₃₄=（a₃₄-q₃₁q₁₄-q₃₂q₂₄）/q₃₃

q₃₅=（a₃₅-q₃₁q₁₅-q₃₂q₂₅）/q₃₃

q₄₄=a₄₄-q₄₁q₁₄-q₄₂q₂₄-q₄₃q₃₄

q₅₄=a₅₄-q₅₁q₁₄-q₅₂q₂₄-q₅₃q₃₄

q₄₅=（a₄₅-q₄₁q₁₅-q₄₂q₂₅-q₄₃q₃₅）/q₄₄

q₅₅=a₅₅-q₅₁q₁₅-q₅₂q₂₅-q₅₃q₃₅-q₅₄q₄₅

LU分解所需的乘除法次数按行和列归纳如下：

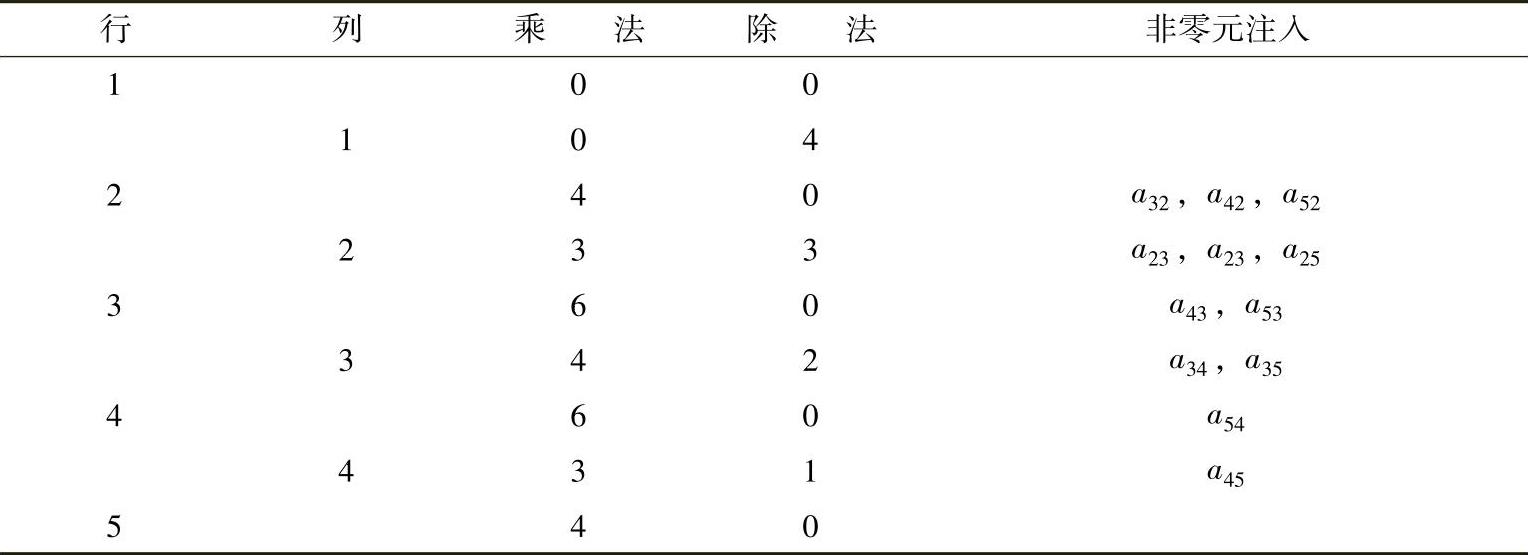
因此LU分解中乘除法次数α=40。前代（Ly=b）和回代（Ux=y）步骤如下：

y₁=b₁/q₁₁

y₂=（b₂-q₂₁y₁）/q₂₂

y₃=（b₃-q₃₁y₁-q₃₂y₂）/q₃₃

y₄=（b₄-q₄₁y₁-q₄₂y₂-q₄₃y₃）/q₄₄

y₅=（b₅-q₅₁y₁-q₅₂y₂-q₅₃y₃-q₅₄y₄）/q₅₅

x₅=y₅

x₄=y₄-q₄₅x5

x₃=y₃-q₃₅x₅-q₃₄x₄

x₂=y₂-q₂₅x₅-q₂₄x₄-q₂₃x₃

x₁=y₁-q₁₅x₅-q₁₄x₄-q₁₃x₃-q₁₂x2

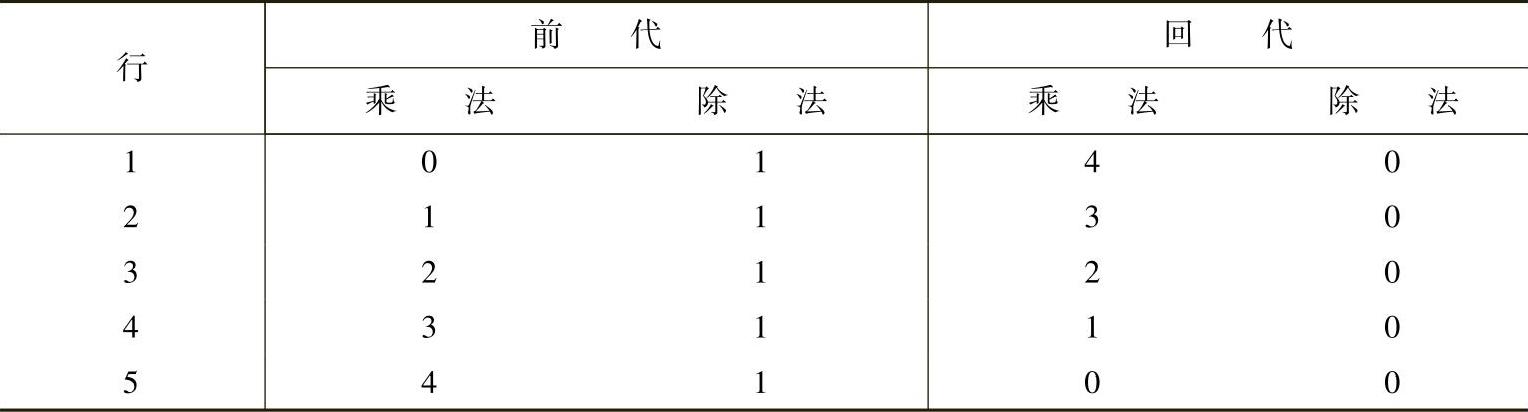
因此前代和回代步骤中的乘除法次数β=25。求解Ax=b所需的乘除法总数为α+β=65。

当原始矩阵中的零元素在LU分解过程中变为非零元素时就产生了非零元注入。此现象可以用图形方法形象化地模拟。将例4.4的图重新画于图4.7。

在此编号方案中，与节点1对应的行和列最先进行三角分解。这相当于把节点1从该图中移除。当节点1被移除时，所有与它相连的节点必须被连接起来。而每增加一条边相当于矩阵Q中增加两个非零元注入（q_ij和q_ji），因为矩阵Q是对称的。节点1移除后的新图如图4.8所示，其中的虚线表示会产生6个非零元注入：q₂₃、q₂₄、q₂₅、q₃₄、q₃₅和q₄₅。这6个非零元注入也同样在该例的求解过程中列出。

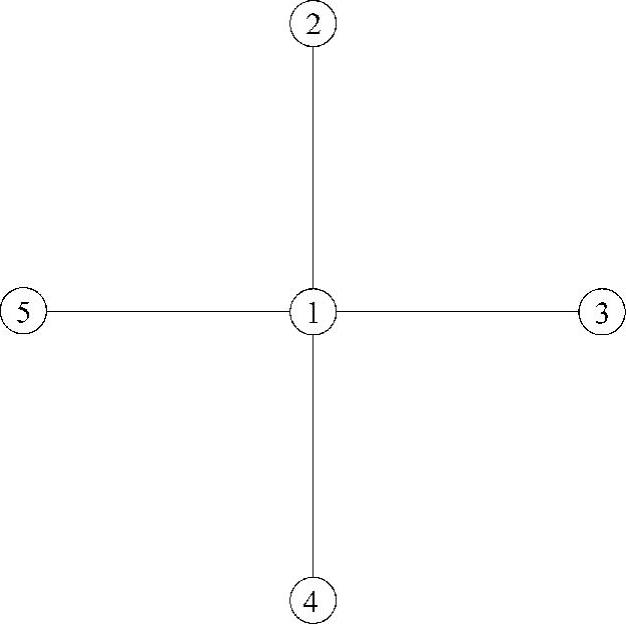
图4.7 例4.4的图

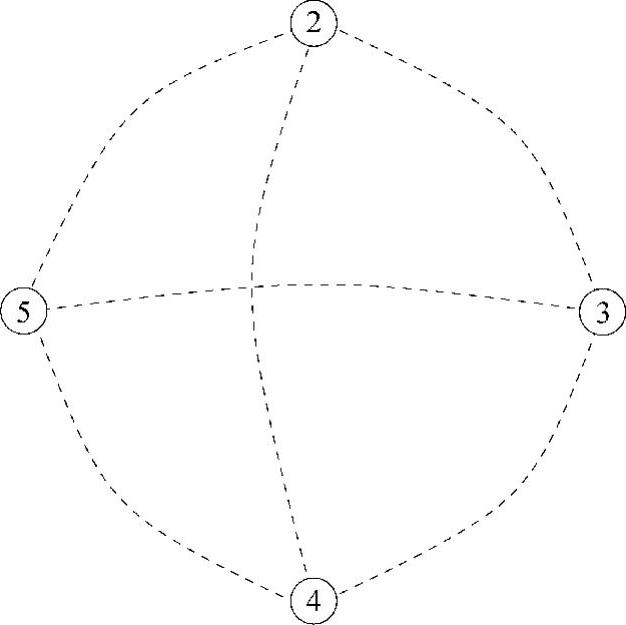
图4.8 移除节点1后产生的非零元注入

例4.5 确定图4.9所示的系统求解过程所需的乘除法次数和非零元注入数目。(www.xing528.com)

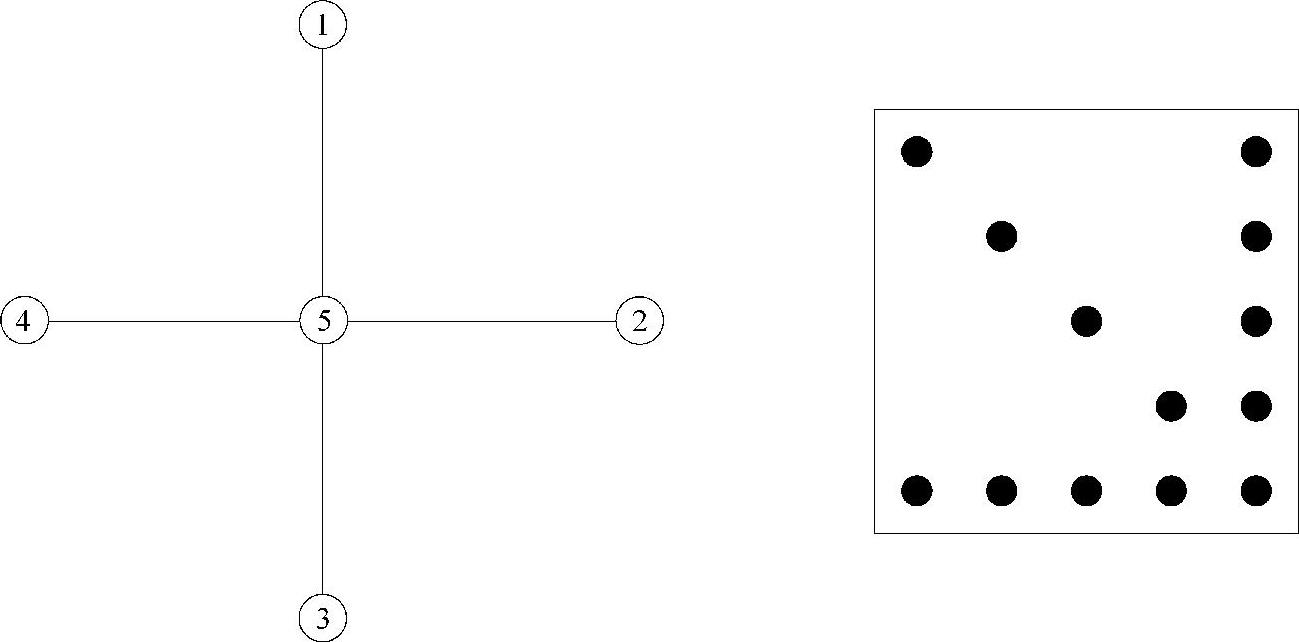
图4.9 例4.5的图与矩阵

解4.5 LU分解的步骤如下：

q₁₁=a₁₁

q₅₁=a₅₁

q₁₅=a₁₅/q₁₁

q₂₂=a₂₂

q₂₅=a₂₅/q₂₂

q₅₂=a₅₂

q₃₃=a₃₃

q₅₃=a₅₃

q₃₅=a₃₅/q₃₃

q₄₄=a₄₄

q₅₄=a₅₄

q₄₅=a₄₅/q₄₄

q₅₅=a₅₅-q₅₁q₁₅-q₅₂q₂₅-q₅₃q₃₅-q₅₄q₄₅

LU分解所需的乘除法次数按行和列归纳如下：

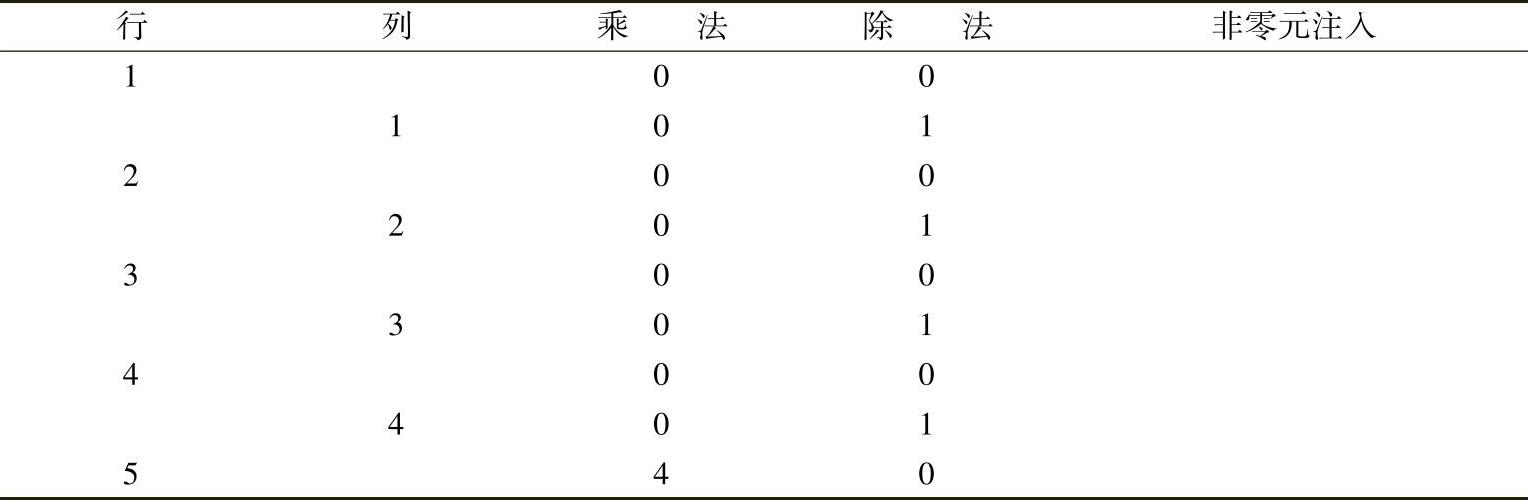
因此LU分解中乘除法次数α=8。前代（Ly=b）和回代（Ux=y）步骤如下：

y₁=b₁/q₁₁

y₂=b₂/q₂₂

y₃=b₃/q₃₃

y₄=b₄/q₄₄

y₅=（b₅-q₅₁y₁-q₅₂y₂-q₅₃y₃-q₅₄y₄）/q₅₅

x₅=y₅

x₄=y₄-q₄₅x₅

x₃=y₃-q₃₅x₅

x₂=y₂-q₂₅x₅

x₁=y₁-q₁₅x5

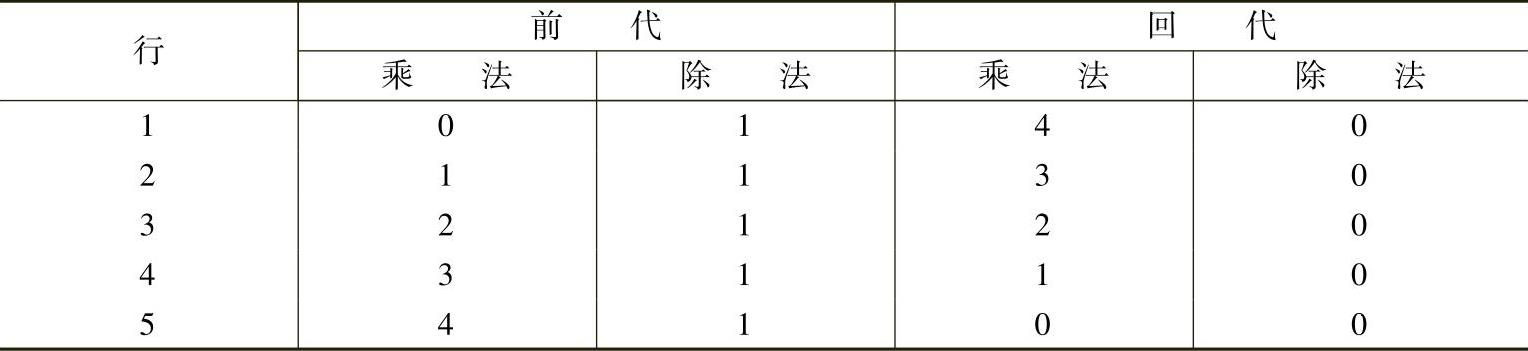
因此前代和回代过程中的乘除法次数β=13。求解Ax=b所需的乘除法总数为α+β=21。

尽管两个原始矩阵有相同数目的非零元，但简单地重新编号矩阵图的顶点就可以使乘除法次数大大减少。产生这种结果的部分原因是LU分解时产生的非零元注入数目减少。例4.4中的矩阵Q变成了满阵，而例4.5中的矩阵Q仍然保持了与原始矩阵A同样的稀疏结构。从这两个例子可以看出，尽管不同的节点排序方案不会影响线性方程求解的精度，但不同的节点排序方案会对求解的速度有很大的影响。一个好的排序方案可以让生成的矩阵Q具有类似于原始矩阵A的稀疏结构，这意味着非零元注入的数目已被最小化。这个目标构成了各种最优排序方案的基础。最优排序问题是一个NP完全问题^[54]，然而已开发出了几种方案可以达到近似最优的结果。

例4.6 确定图4.10在当前排序方案下的α、β和非零元注入数目。

解4.6 第一步是确定LU分解中哪儿会产生非零元注入。通过观察，发现非零元注入会出现在如图4.11所示矩阵中用△标示的位置。根据图4.11，非零元注入的数目为24。

可以依据包含非零元注入的矩阵，用一种简单的方法直接计算出α和β，而不采用常规方法计算LU分解和前代/回代过程中所需的乘除法次数。

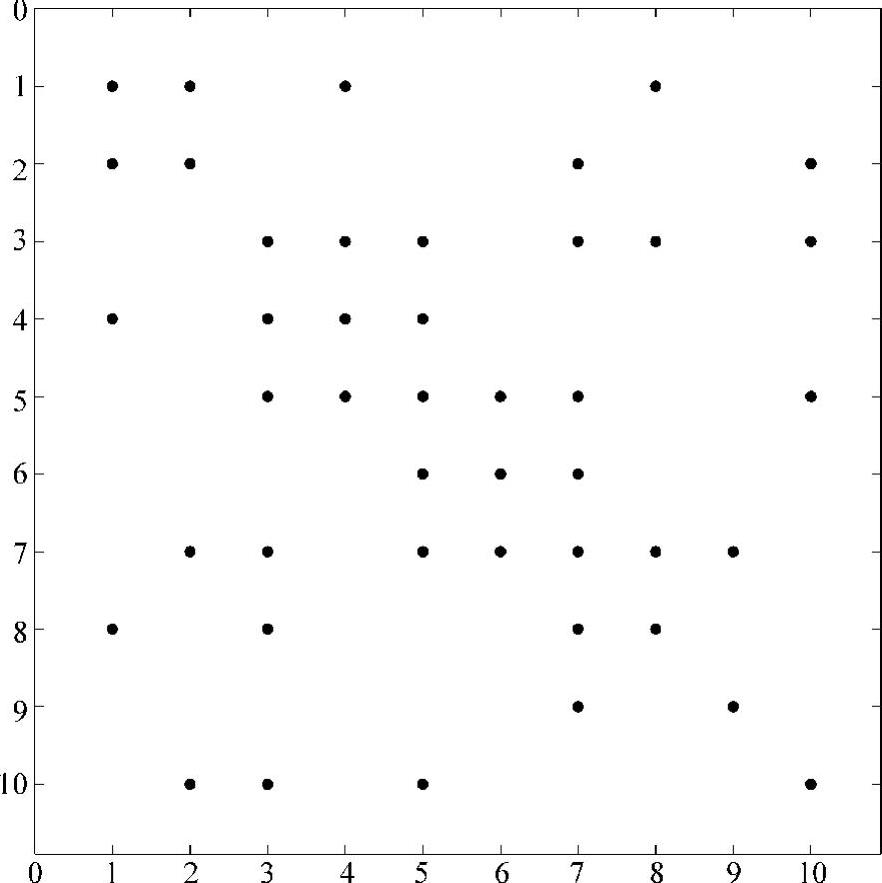
图4.10 例4.6的矩阵

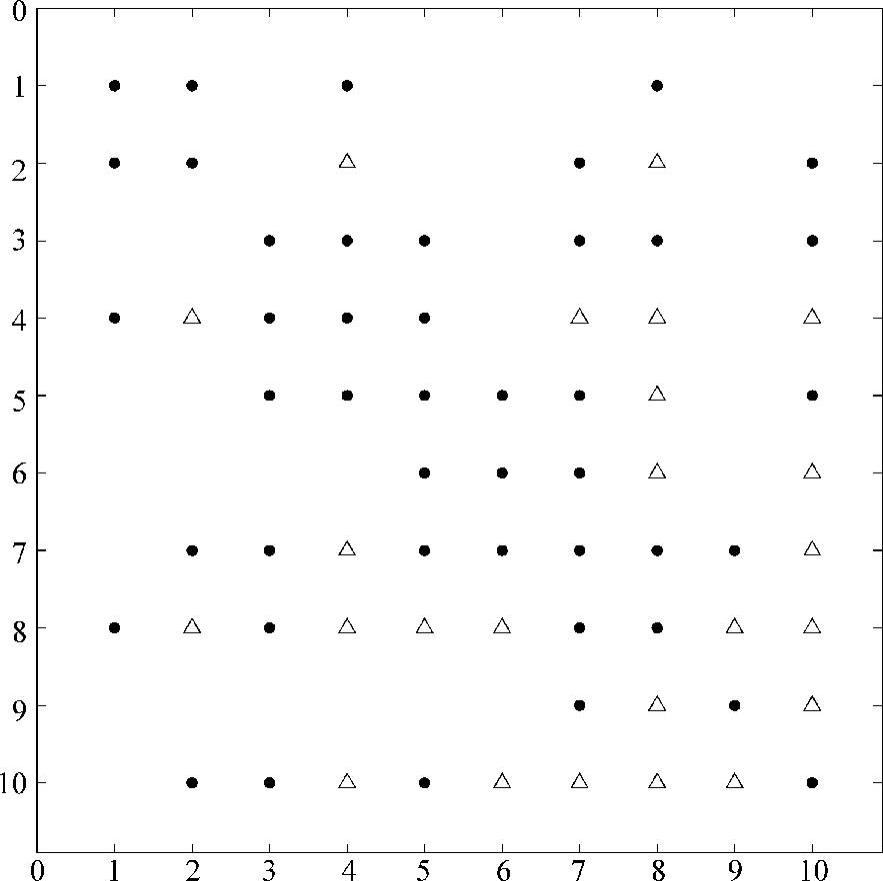
图4.11 加入非零元注入后例4.6的矩阵

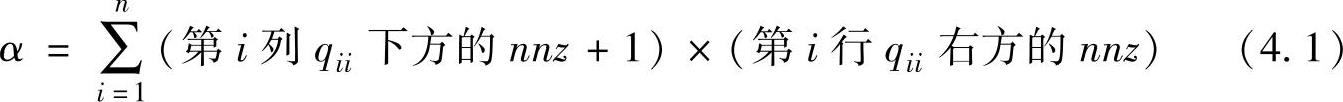
β=矩阵Q的nnz值 （4.2）

利用式（4.1）和式（4.2），对于图4.11所示的矩阵Q，

α=（3×4）+（4×5）+（5×6）+（4×5）+（4×5）+（3×4）+

+（3×4）+（2×3）+（1×2）+（0×1）=134

而

β=nnz=68

因此

α+β=202

请将此结果与α+β=430做对比。

即使没有最优排序，稀疏矩阵求解也会减少超过50%的计算量。最优排序方案的目标之一是使分解后的矩阵Q具有最少的非零元注入，从而使乘除法次数α最小。最优排序方案的第2个目标是使前代/回代过程中的乘除法次数β最小化。根据这个双重目标已提出了几种最优排序方案。