PV曲线与连续潮流计算探究

潮流计算是用于监视系统电压随负荷变化的一个有力工具。一种常见的用法是画出某个特定母线的电压随负荷从基准值增长到极限点（通常被称为最大负荷点）时的变化曲线。如果负荷首先从基准值增大到极限负荷点，然后又从极限负荷点逐步减小到基准值，就可以画出完整的功率-电压关系曲线，即PV曲线。这条曲线，如图3.14所示，有时因其形状特征而被称为“鼻子曲线”。

在极限负荷点，即鼻子曲线的顶点上，系统潮流方程的Jacobi矩阵将变为奇异，因为鼻子曲线的斜率将变为无穷大。因此，用于求解潮流的传统Newton-Raphson法将会失效。这种情况下，需要采用一种被称为“连续法”的改进Newton-Raphson法。连续法在基本潮流方程中引入了一个附加方程和一个未知量。该附加方程是特别选择的，以保证增广的Jacobi矩阵在负荷极限点不再奇异。附加的未知量通常被称为连续参数。

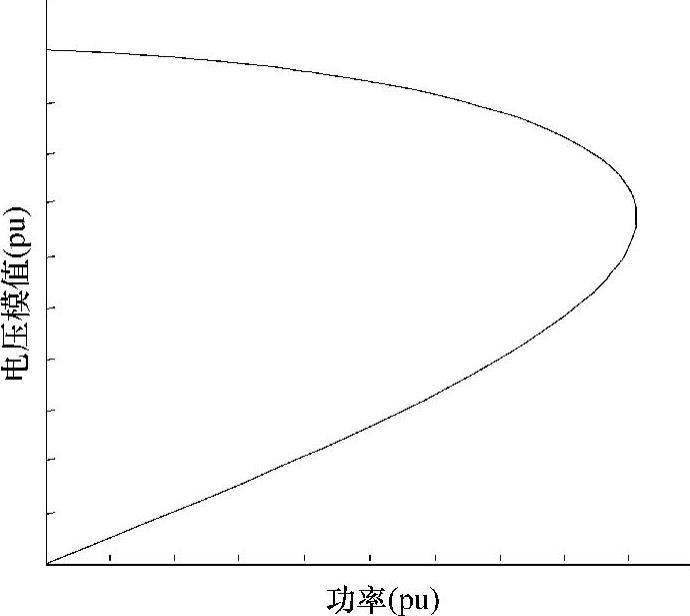
图3.14 PV曲线

连续法通常依赖于预测-校正方案以及必要时改变连续参数的规则。跟踪PV曲线的基本做法是选择一个新的连续参数值（功率或电压），然后预测此参数值下的潮流解。这通常可以用切线（即线性）逼近来完成。将此预测值作为初始值进行非线性迭代，然后求出增广潮流方程的解（即校正）。所以此方案是先预测后校正。这种预测-校正方案如图3.15所示。令潮流方程组用下式来表达

λK-f（δ，V）=0 （3.161）

或者

F（δ，V，λ）=0 （3.162）

式中，K是可变负荷分布特性（即基准状态下P与Q的关系），λ是负荷参数，从1（基准点）变化到负荷极限点时的值。式（3.162）可以进行线性化，得

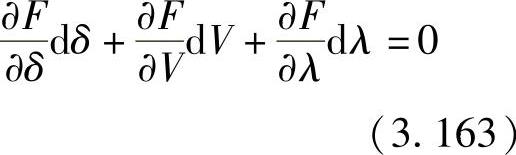
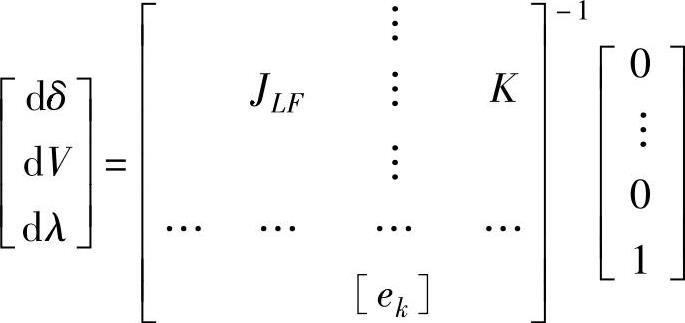
式（3.163）未知量比方程个数多1个（多了未知量λ），因此需要增加1个方程：

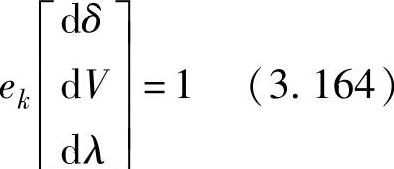
式中，e_k是一个行向量，除了被选作连续参数的未知量的位置为+1或者-1外，其他元素都为0。而+1或者-1的选择取决于连续参数是增加还是减小。当连续参数λ表示功率时，正号表示负荷是增加的。当连续参数表示电压时，负号表示电压模值减小。

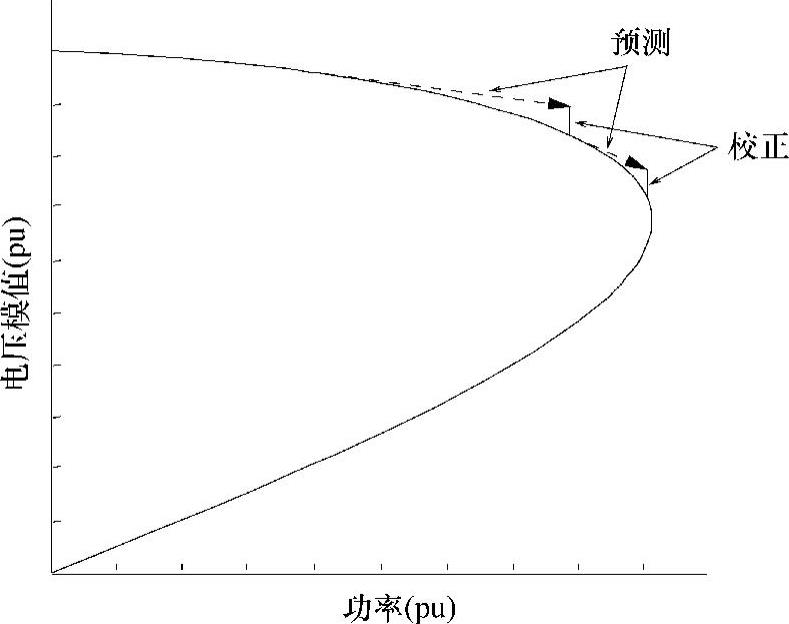
图3.15 预测-校正方案

未知量按如下方式预测：

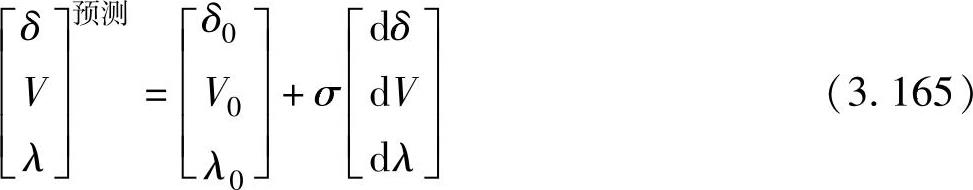
式中，

而σ是本次预测的步长。注意，连续参数对应的状态dx_k=1，所以

x_k^预测=x_k0+σ

因此，σ作为步长应基于连续参数所表示的量（通常是功率或电压）进行合理的选择。

校正环节涉及求解如下方程组：

F（δ，V，λ）=0 （3.166）

x_k-x_k^预测=0 （3.167）

式中，x_k是选择的连续参数。一般地，连续参数被选择为呈现最大变化率的状态。

例3.13 应用连续潮流法画出图3.16所示系统的PV曲线，设负荷从0变化到最大负荷点。

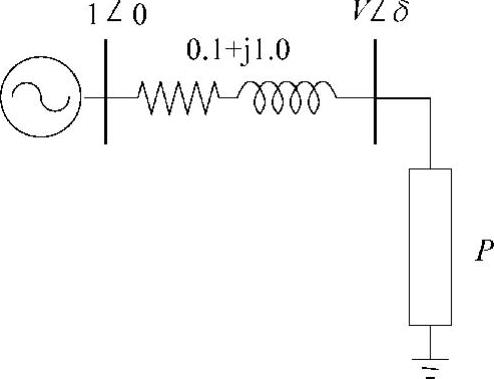
图3.16 例3.13的系统图

解3.13 图3.16所示系统的潮流

方程为

0=-P-0.995Vcos（δ-95.7°）

-0.995V²cos（84.3°）（3.168）

0=-0.995Vsin（δ-95.7°）

-0.995V²sin（84.3°）（3.169）

在连续潮流法求解过程中，注入有功功率和无功功率向量将用向量λK代替。负荷向量λK为

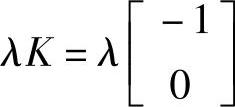
式中，λ将从0变化到最大负荷值。一般地，向量K将包含系统中所有注入有功功率和无功功率的基准值。在本例中，负荷P对应位置的元素是负的，表示注入的功率是负的（即是负荷）。

上述潮流方程组的Jacobi矩阵为

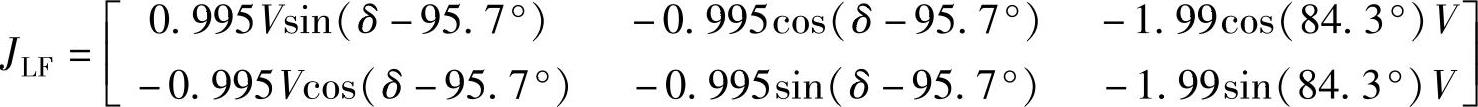
第1次迭代(www.xing528.com)

初始时，连续参数选择λ，因为在远离鼻子曲线顶点的地方，负荷比电压变化得更快。在λ=0点，电路处于空载状态，初始的电压模值和相角为1∠0°。取σ=0.1pu，预测环节为

式中，δ的单位是rad。注意，λ的预测值是0.1pu。

校正环节求解方程组：

0=-λ-0.995Vcos（δ-95.7°）-0.995V²cos（84.3°） （3.173）

0=-0.995Vsin（δ-95.7°）-0.995V²sin（84.3°） （3.174）

式中，取负荷参数λ为0.1pu。注意，这是一个常规的潮流计算问题，不需要改变程序就能够求解。

第1次校正后得到

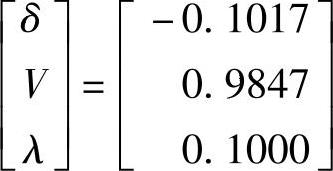
注意，这个过程与图3.15所展示的是一致的。预测环节的步长σ是沿着该点PV曲线的切线的。校正环节将会沿着垂直路径，因为功率（λK）在校正过程中保持恒定。第2次迭代

第2次迭代类似于第1次迭代。预测环节产生如下的猜想值：

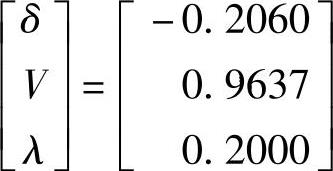
式中，λ按照步长σ=0.1pu增加。

对上述猜想值进行校正得到第2组更新值为

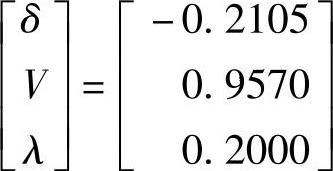
第3次和第4次迭代

第3次和第4次迭代与前面的迭代是类似的，到此为止的结果总结如下：

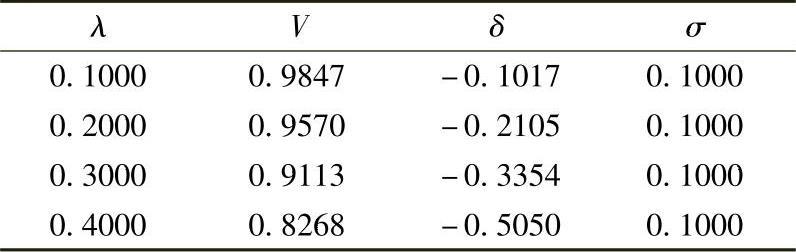
超过这个点后，对于σ=0.1的步长，潮流不收敛。此方法已经接近最大功率点（鼻子曲线的顶点），这可以从λ相对小的变化就会引起电压快速下降看出。在这点上，为了保证校正环节的收敛，连续参数将从λ切换到V。因此，预测环节改变为

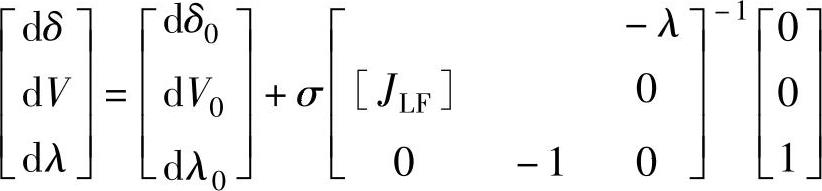
式中，最后一行（行向量e_k）的-1对应于V而不是λ，负号表示预测环节将减小电压模值一个步长σ。对应于电压模值的改变，σ改变为0.025是更合适的。

当连续参数切换到电压模值后，校正环节也需要改变，新的增广方程组变为

0=f₁（δ，V，λ）=-λ-0.995V（cos（δ-95.7°）+Vcos（84.3°）） （3.175）

0=f₂（δ，V，λ）=-0.995Vsin（δ-95.7°）-0.995V²sin（84.3°） （3.176）

0=f₃（δ，V，λ）=V-V^预测 （3.177）

这组方程因最后一个方程的原因，不能用传统的潮流计算程序求解，但最后一个方程对保证用Newton-Raphson法迭代非奇异是必要的。幸运的是，Newton-Raphson法所用的迭代矩阵与预测矩阵是相同的：

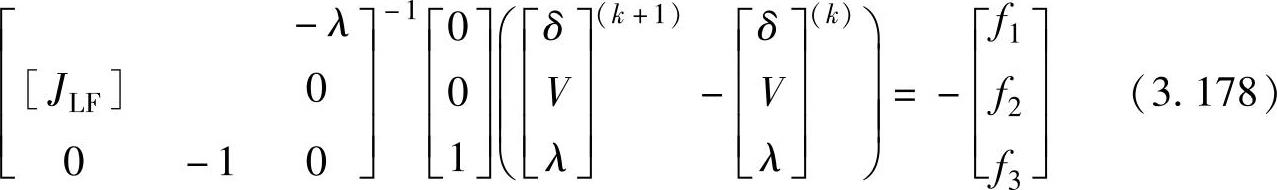
从而能使计算量最小化。

注意，现在的校正环节是在水平方向上的校正，因为电压模值已固定，而需要对λ和δ进行校正。相应的迭代值如下：

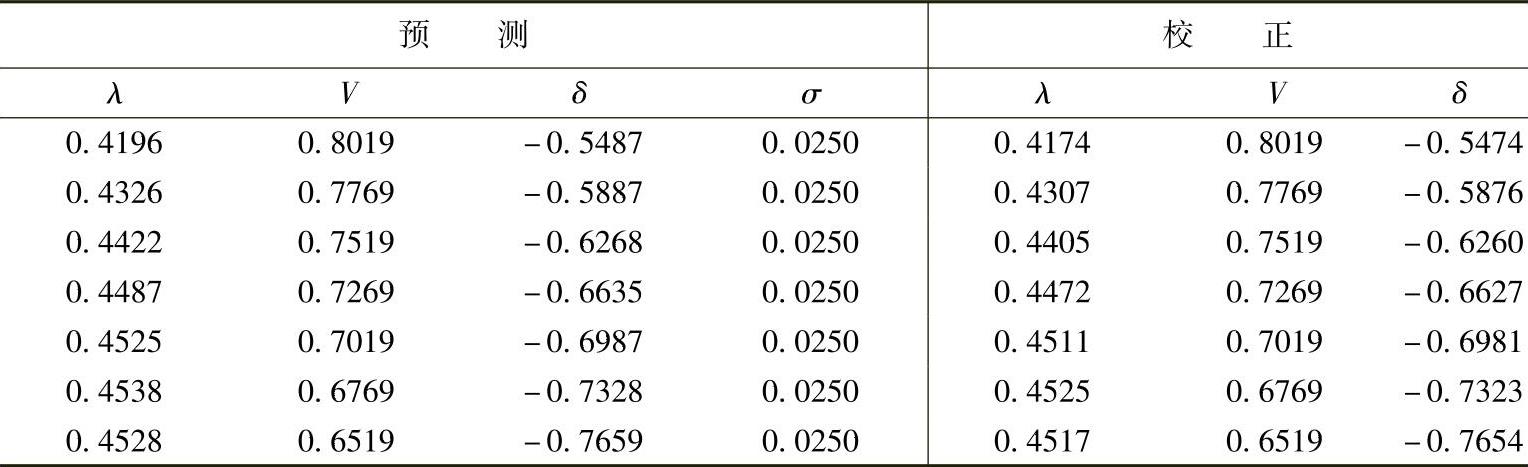
注意，最后一个迭代值，负荷参数λ已经开始随着电压的下降而下降。这表示连续潮流计算已经开始画出鼻子曲线的下半支。但是，由于迭代还是在鼻子曲线的顶点附近，Jacobi矩阵将仍然是病态的，因此在将连续参数从电压模值切换回λ之前，再继续进行几步迭代是一种好的思路。继续迭代的结果为

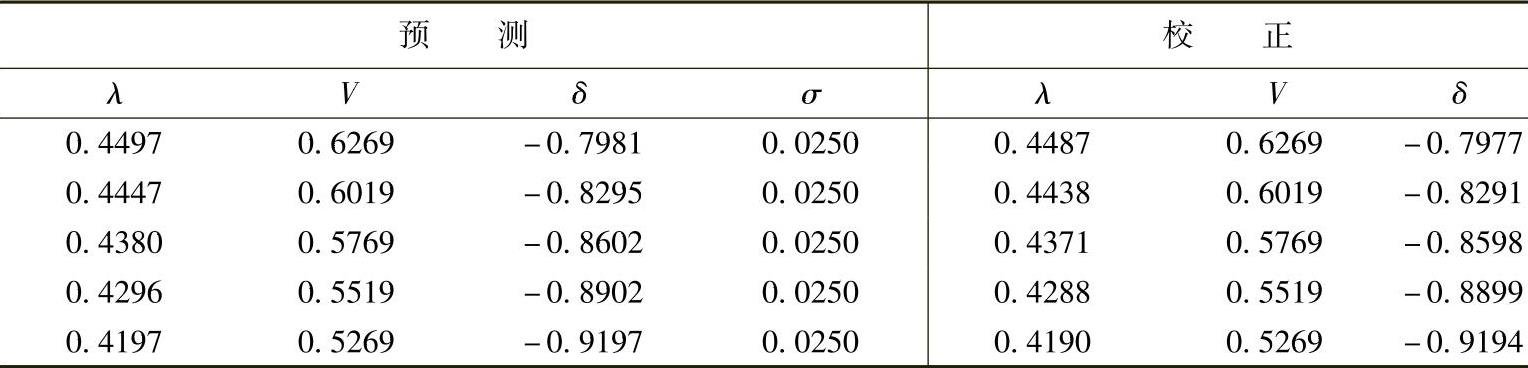
将连续参数切换回λ后，向量e_k变为

e_k=[0 0 -1]

式中，-1表示连续参数λ将减小（即功率减小到基准值）。预测校正过程与前面的一样，所得结果如下：

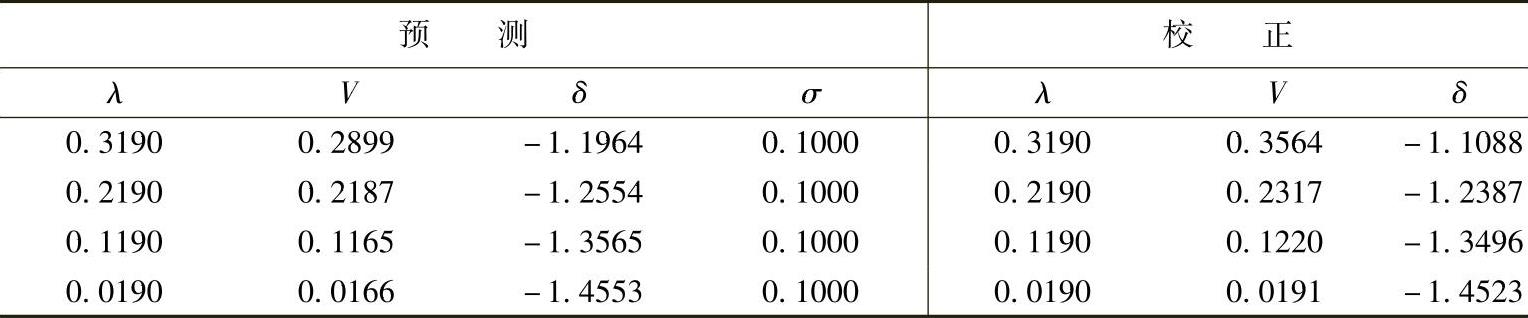
这些结果合并在一起构成了如图3.17所示的PV曲线。注意在PV曲线顶点附近当连续参数从λ切换到电压时的步长改变。如何选择合适的步长是与问题相关的，为了提高计算效率可以自适应地改变。

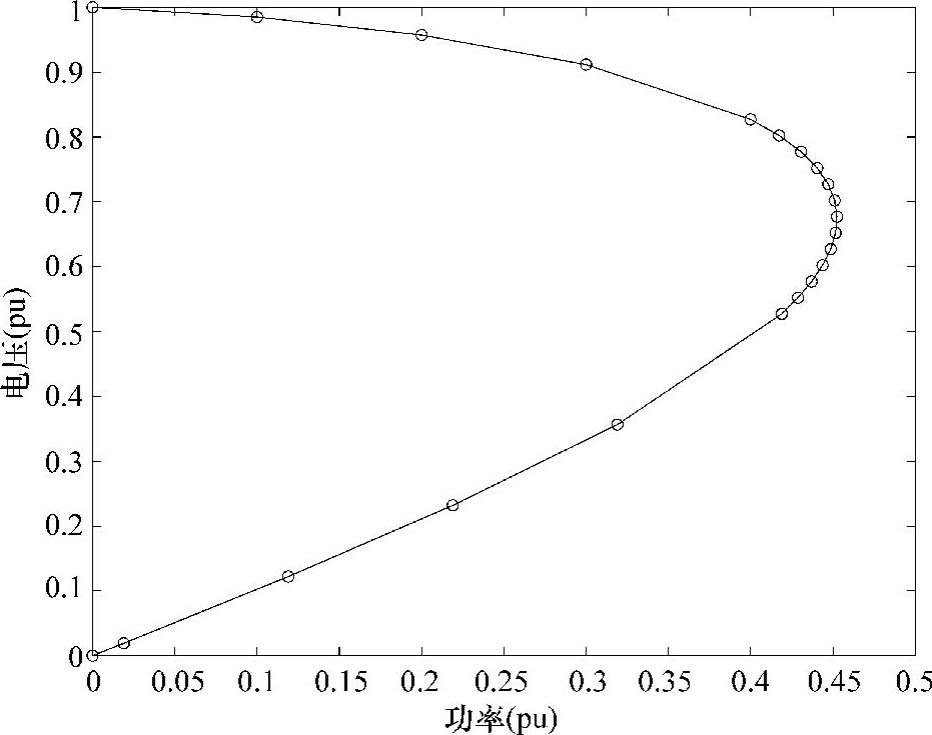
图3.17 例3.13系统的PV曲线