调节变压器在电力网络中的作用及计算方法

电力网络中最常见的控制器之一是“调节变压器”。这是一种响应于负荷侧电压变化而改变匝数比（分接头档位）的变压器。如果二次侧（负荷侧）电压低于期望的电压（例如在重载情况下），分接头将会改变，在保持一次侧电压的条件下提高二次侧电压。调节变压器经常也被称为有载分接头变化（ULTC）变压器。分接头档位t可以是实数也可以是复数，在标幺制下，匝数比被定义为1∶t，其中t的典型值在1.0的10%范围内。通过将t定义为具有模值和相角的复数，就可以实现对移相变压器的模拟。

调节变压器的作用通过导纳矩阵而纳入到潮流计算中。为了将调节变压器归入到导纳矩阵中，将调节变压器看作为一个两端口网络，端口电流为I_i和I_j，端口电压为V_i和V_j，如图3.13所示。

受端电流为

I_j=（V_j-tV_i）Y （3.117）

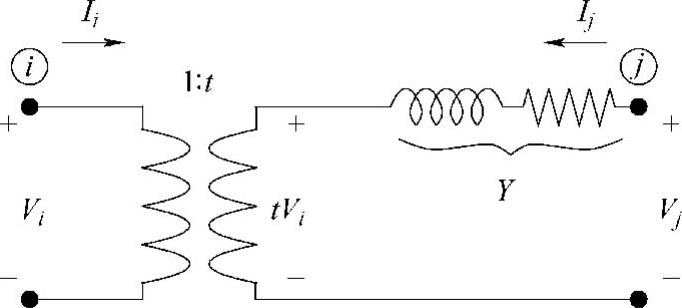
图3.13 调节变压器模型

注意，电流也可以通过功率传输方程获得

S_i=V_iI_i^∗=-tV_iI_j^∗ （3.118）

因此，

I_i=-t^∗I_j （3.119）

=-t^∗（V_j-tV_i）Y （3.120）

=tt^∗YV_i-t^∗YV_j （3.121）

=|t|²YV_i-t^∗YV_j （3.122）

因此，导纳矩阵中的非对角元为

Y（i，j）=-t^∗Y

Y（j，i）=-tY

而Y（i，i）上需要加上|t|²Y，Y（j，j）上需要加上Y。

因为调节变压器是作为电压控制装置使用的，计算上的一种常用做法是求分接头档位t使得二次侧母线的电压模值V_j为一个特定值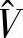。这可以理解为在系统方程中增加一个附加变量t和一个附加约束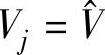。由于附加约束刚好由附加的自由度平衡，因此未知量与方程个数保持相同。存在两种主要的方法来求解分接头档位t使之满足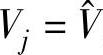。一种方法是迭代法，另一种方法直接从潮流方程计算t。

迭代法可以总结为如下步骤：

（1）令t=t₀

（2）求解一次潮流以求出Vj

（3）判断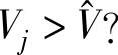，如果是，那么t=t-Δt，转第（2）步

（4）判断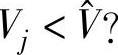，如果是，那么t=t+Δt，转第（2）步

（5）结束

这种方法概念上是简单的，并且不需要改变潮流算法。但是，如果t₀远离所求的档位，这种方法可能需要计算很多次潮流。(www.xing528.com)

直接法将Newton-Raphson法直接应用到包含分接头档位t的新的潮流方程上。其步骤为

（1）令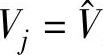，并设t为一个未知状态量

（2）改变Newton-Raphson法的Jacobi矩阵，将相对于V_j求偏导数的行用相对于t求偏导数的行代替

（3）改变状态向量x为

注意，状态V_j已用t代替。

（4）用Newton-Raphson法求解

在这种情况下，潮流方程只计算一次，但是由于系统的Jacobi矩阵改变了，不能使用标准的潮流计算程序。

由于分接头不能沿着变压器绕组连续移动，而是垂直地从一个绕组移动到相邻绕组，实际的档位是一个非连续状态量。因此，在上述两种情况下，计算得到的分接头档位必须舍入到可能的最接近的物理档位。

例3.10 对于图3.12中的系统，在母线3和负荷之间引入一个新的母线4，在母线3和母线4之间加入一个变压器，其电抗为X，分接头为实数t。求新的导纳矩阵和相应的Jacobi元素。

解3.10 令包含母线1-3的子系统的导纳矩阵为

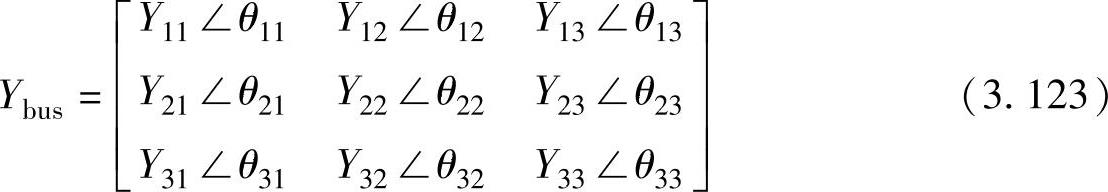
在母线3和4之间加入变压器后产生的新的导纳矩阵为

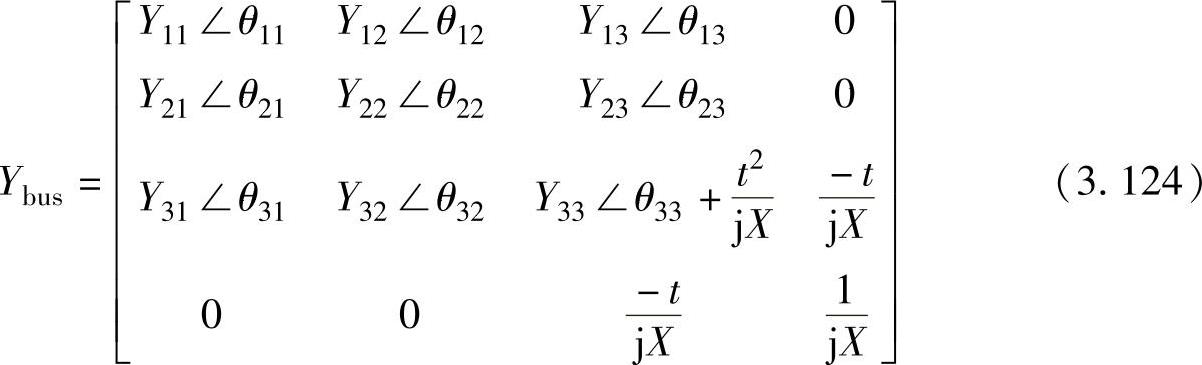
母线3上的潮流方程变为

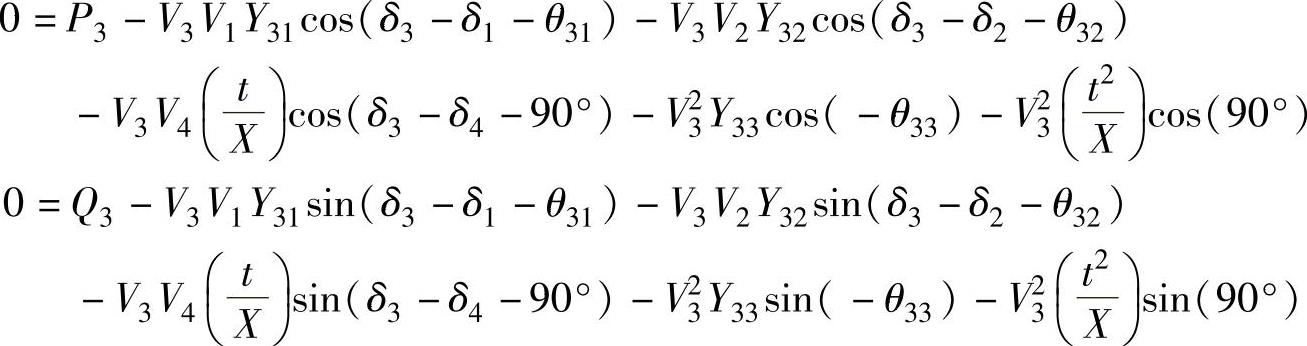
由于V₄是固定的，因此没有偏导数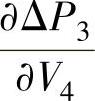，相反，有一个相对于t的偏导数：

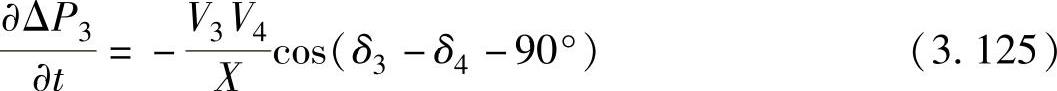
类似地，偏导数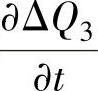为

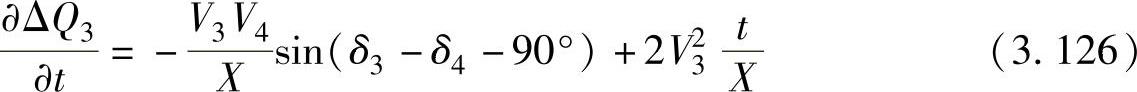
相对于δ₁、δ₂、V₁和V₂的偏导数没有变化，但相对于δ₃、δ₄和V₃的偏导数变为

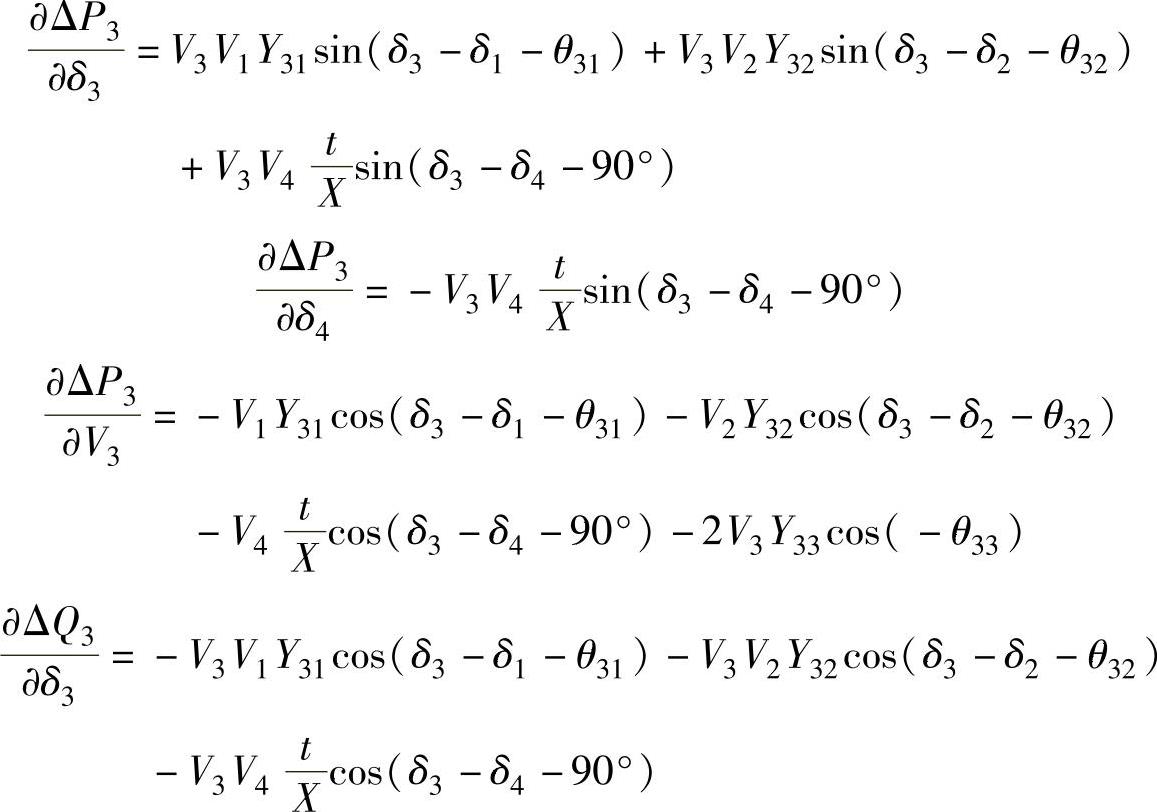
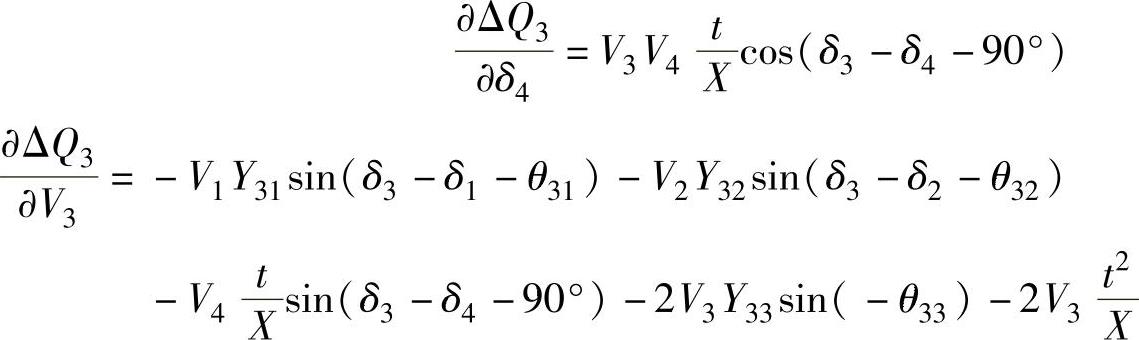
这些偏导数用于建立Newton-Raphson法的Jacobi矩阵，并用于求解潮流方程。