潮流计算问题及解析方法

很多电力系统问题归结为一组非线性方程组的求解。可能电力系统中最常见的非线性问题是潮流计算问题。潮流计算问题的基本原理是，给定系统负荷、发电出力和网络结构，就能根据非线性的潮流方程求解母线电压和线路潮流。建立潮流方程的典型方法是对整个系统中的每一个母线应用Kirchoff定律。在此情景下，Kirchoff定律可以理解为“进入一个母线的功率之和必须等于零”，即每个母线上的功率是守恒的。由于功率由有功功率和无功功率两个分量组成，每个母线就对应两个方程，一个对应于有功功率，另一个对应于无功功率。这些方程被称为“潮流方程”：

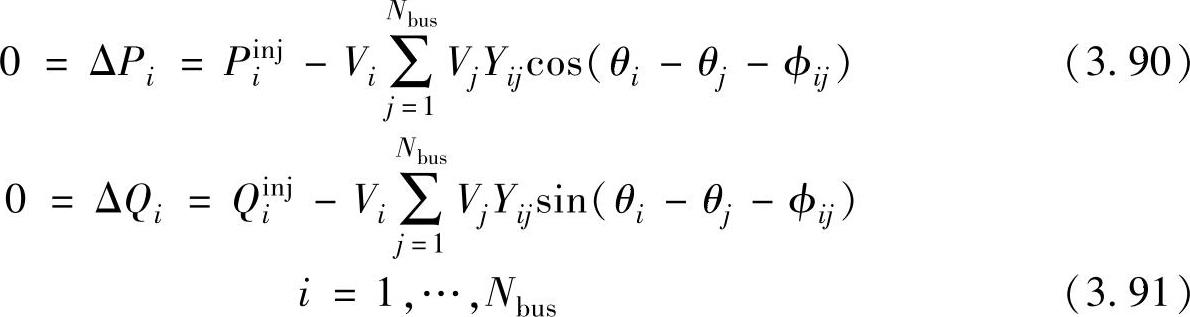
式中，P_i^inj、Q_i^inj分别是注入母线i的有功功率和无功功率，负荷被模拟成负的功率注入；V_i和V_j分别表示母线i和母线j的电压模值；θ_i和θ_j分别表示母线i和母线j的电压相角；Y_ij∠ϕ_ij是网络导纳矩阵Y位于第i行、第j列位置上的元素；常数N_bus是整个系统的母线个数；式（3.90）和式（3.91）中的ΔP_i和ΔQ_i被称为偏差项，它们给出了根据电压模值和相角计算得出的功率值与实际注入功率之间的偏差。随着Newton-Raphson法迭代的继续，上述偏差值将被驱动到零，使根据电压模值和相角计算得到的离开母线的功率等于注入母线的功率。此时，已收敛的电压模值和相角被用来计算线路潮流、发电机母线的注入无功功率以及平衡母线的功率等。

式（3.90）和式（3.91）被称为是潮流方程的“极坐标”形式，如果将Y_ij∠ϕ_ij用直角坐标复数g_ij+jb_ij表示，那么潮流方程可以写成“直角坐标”形式：

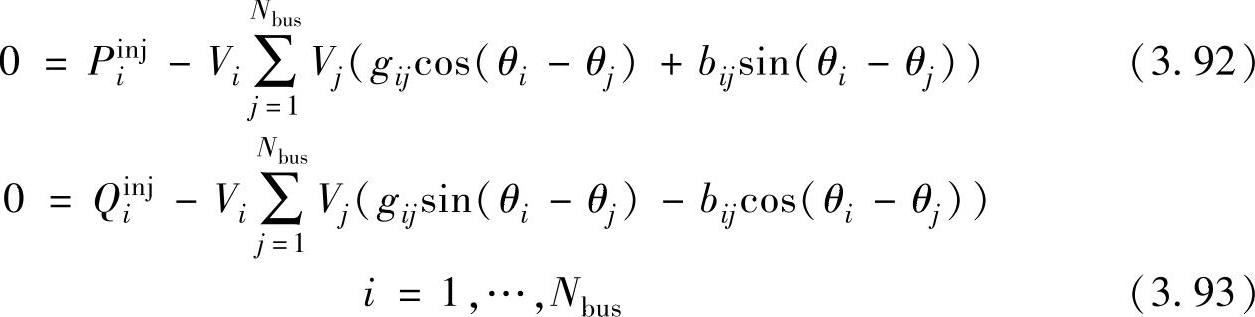
在上述任何一种情况下，潮流方程都是一组非线性方程组，它们在电压和相角两方面都是非线性的。这组方程最多有2N_bus个方程。对于每个已知电压的母线（电压控制母线）可以除去一个潮流方程；而对于平衡母线，因相角已知，也可以除去一个潮流方程；因此，潮流方程组中的方程个数可以减少。这种方程数的减少是必要的，因为对于完全确定的方程组，方程的个数必须与未知量的个数相等。一旦建立起非线性的潮流方程组，就可以直接应用Newton-Raphson法进行求解。

采用Newton-Raphson法求解潮流方程的最常见做法是，将方程整理成先电压相角后电压模值的形式，即

式中，

Δδ_i=δ_i^k+1-δ^k_i

ΔV_i=V_i^k+1-V^k_i

这些方程然后通过LU分解和前代/回代进行求解。而Jacobi矩阵通常被分为4个分块，为

每个分块表示一种偏差方程相对于一种未知量的偏导数。这些偏导数具有8种类型，即每种偏差方程对应2种偏导数，其中一个对应对角元，而另一个对应非对角元。这些偏导数总结如下：

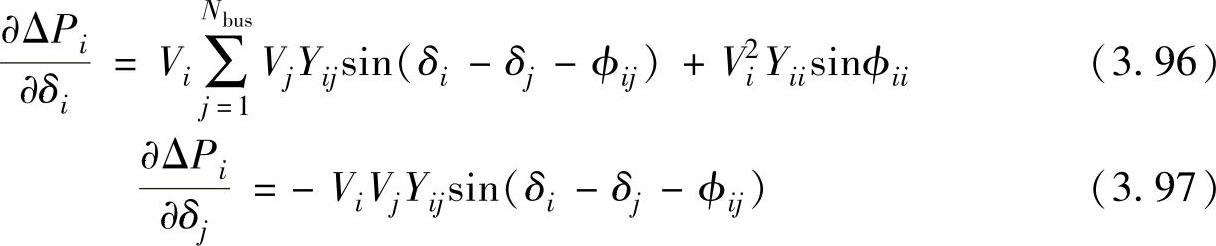
对潮流方程求解的一种常见改进是将未知增量ΔV_i用标幺值来代替。这种改变将产生一个更加对称的Jacobi矩阵，因为现在Jacobi矩阵的分块J₂和J₄需要乘上V_i以补偿对ΔV_i除以V_i标度的改变。这样，分块中的所有偏导数都变成了电压模值的二次式。

用于求解潮流方程的Newton-Raphson法编程实现是相对简单的，因为函数值计算和偏导数计算使用的是相同的表达式。因此，一旦计算出偏差方程，计算Jacobi矩阵的附加计算量是很小的。

例3.9 对图3.12所示的小型电力系统求电压模值、相角和线路潮流，系统的标幺值参数如下：

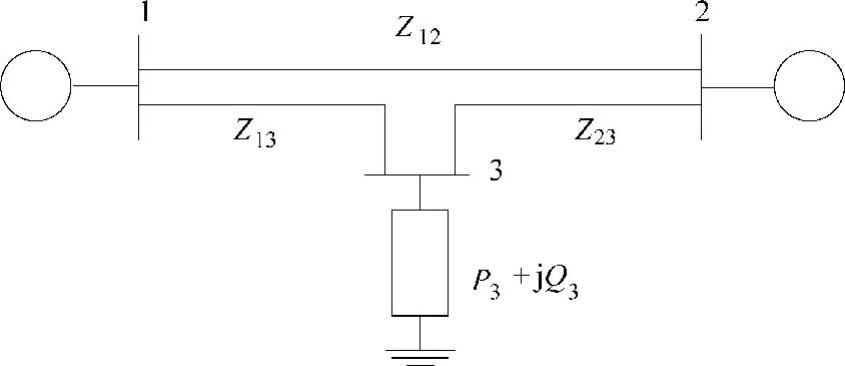
图3.12 算例电力系统

解3.9 潮流计算的第一步是计算系统的导纳矩阵Y。计算导纳矩阵元素的一种简单方法是

Y（i，j）母线i和j之间导纳的负值；

Y（i，i）连接到母线i的所有导纳之和。

计算此系统的导纳矩阵得

通过观察，此系统有3个未知量：δ₂、δ₃和V₃，因此需要3个潮流方程。这些潮流方程为

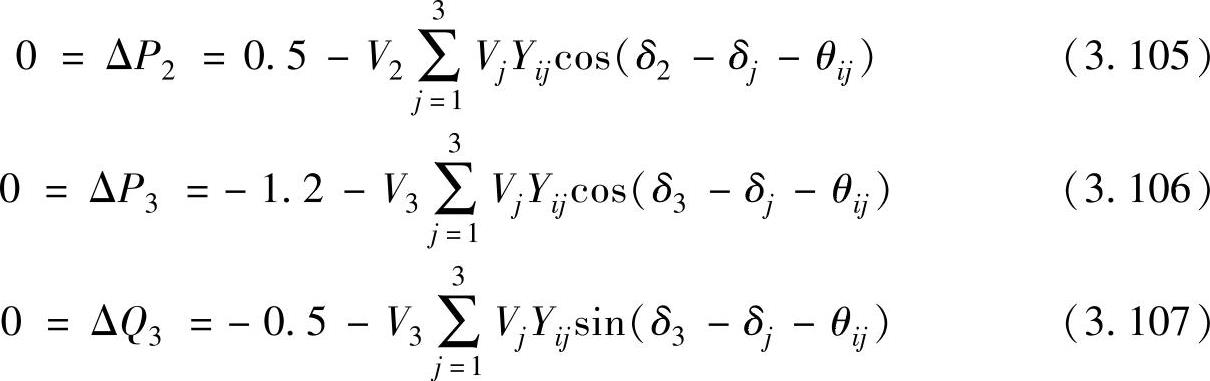
将已知量V₁=1.02、V₂=1.00和δ₁=0以及导纳矩阵的元素代入上述方程，得到

ΔP₂=0.5-（1.00）（（1.02）（3.3260）cos（δ₂-0-93.8141°）+（1.00）（13.1505）cos（δ₂-δ₂+84.7148°）+（V₃）（9.9504）cos（δ₂-δ₃-95.7106°）） （3.108）

ΔP₃=-1.2-（V₃）（（1.02）（9.9504）cos（δ₃-0-95.7106°）+（1.00）（9.9504）cos（δ₃-δ₂-95.7106°）+（V₃）（19.8012）cos（δ₃-δ₃+84.2606°）） （3.109）

ΔQ₃=-0.5-（V₃）（（1.02）（9.9504）sin（δ₃-0-95.7106°）+（1.00）（9.9504）sin（δ₃-δ₂-95.7106°）+（（V₃）（19.8012）sin（δ₃-δ₃+84.2606°）） （3.110）

这样，此系统的Newton-Raphson法迭代式为

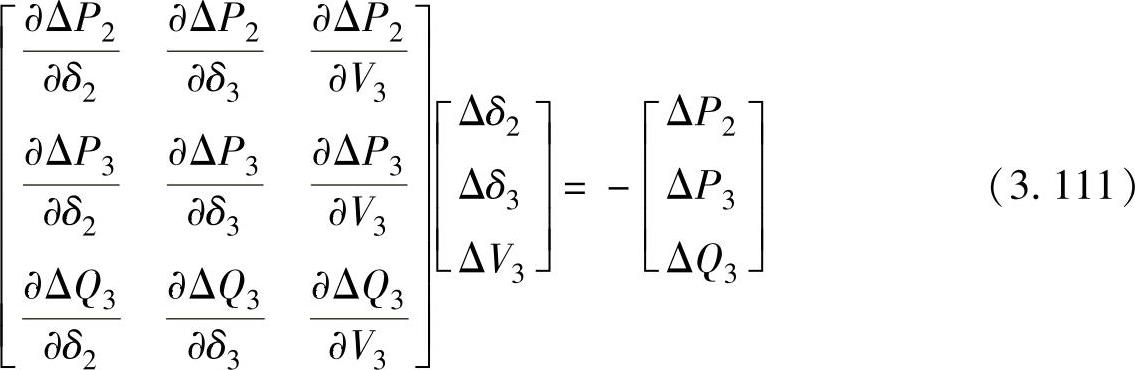
式中，

回想一下，Newton-Raphson迭代法的一个基本假设是，只有当方程组的初始解足够靠近真解时，Taylor级数展开的高次项才可以忽略。在大多数运行状态下，系统中所有母线的电压在±10%额定电压范围内，因此标幺值电压0.9pu≤V_i≤1.1pu。类似地，在大多数运行状态下，系统中相邻母线的相角差通常是很小的。这样，如果将平衡母线的相角设为0，那么系统中所有母线的相角都接近于0。因此，对潮流计算的初始化通常选择“平启动”的初始条件，即所有母线的电压模值等于1.0pu，而所有母线的电压相角等于0。第1次迭代

在平启动初始条件下计算Jacobi矩阵和偏差方程得到

求解

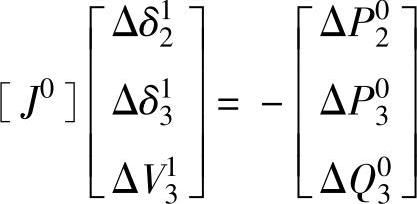(www.xing528.com)

通过LU分解求出方程的解为

因此，

δ₂¹=δ⁰₂+Δδ₂¹=0-0.0096=-0.0096

δ₃¹=δ⁰₃+Δδ₃¹=0-0.0621=-0.0621

V₃¹=V⁰₃+ΔV₃¹=1-0.0163=0.9837

注意，求出的相角是弧度而不是度。第1次迭代的误差取最大的偏差方程绝对值，其值为

ε¹=1.1802

对此过程的一种快速检查法是注意电压更新值V₃¹略小于1.0pu，对于本例的系统结构这是意料中的。还请注意Jacobi矩阵的对角元在绝对值上都大于或等于非对角元，这是因为对角元是各项之和，而非对角元则是单独一项。第2次迭代

以更新后的值δ₂¹、δ₃¹和V₃¹计算Jacobi矩阵和偏差方程得到

求解更新值得到

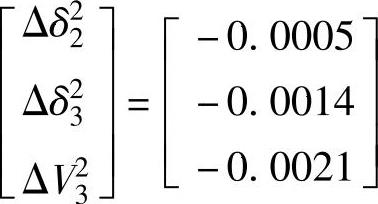
和

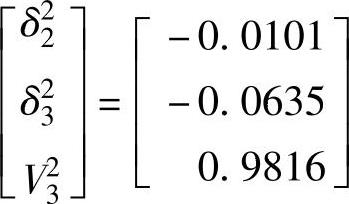
其中，ε²=0.0359

第3次迭代

以更新后的值δ²₂、δ²₃和V²₃计算Jacobi矩阵和偏差方程得到

求解更新值得到

和

其中，

ε³=0.9084×10^-4到此，迭代已经收敛，因为偏差量已足够小，而且更新值的变化已不大。

潮流计算的最后一个任务是计算发出的无功功率、平衡母线的有功功率以及线路潮流。发出的功率可直接通过潮流方程进行计算：

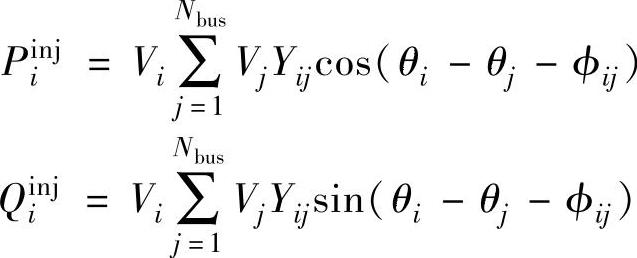
因此，

P_gen，1=P₁^inj=0.7087

Q_gen，1=Q₁^inj=0.2806

Q_gen，2=Q₂^inj=-0.0446

系统中的有功损耗等于发出的有功功率之和减去负荷的有功功率之和，对于本例为

P_loss=∑P_gen-∑P_load=0.7087+0.5-1.2=0.0087pu （3.112）

线路i-j上的损耗需要同时计算线路送端和受端的功率，从母线i送出到母线j的功率为

S_ij=V_i∠δ_iI_ij^∗（3.113）

母线j从母线i得到的功率为

S_ji=V_j∠δ_jI_ji^∗（3.114）

因此，

P_ij=V_iV_jY_ijcos（δ_i-δ_j-ϕ_ij）-V²iYijcos（ϕ_ij） （3.115）

Q_ij=V_iV_jY_ijsin（δ_i-δ_j-ϕ_ij）+V²iYijsin（ϕ_ij） （3.116）

类似地，可以得到P_ji和Q_ji的表达式。在特定线路上的有功功率损耗是从i送出的有功功率与从j受入的有功功率之差。无功功率损耗的计算比较复杂，因为必须考虑线路本身的充电无功（并联电容）。