数值微分法及其在多项式导数逼近中的应用

使用Newton-Raphson法或任何其改进方法需要计算大量的偏导数。在很多情况下，用解析方法求偏导数可能是极其困难的或者计算代价极其高昂。在这些情况下，希望通过函数f（x）直接用数值方法来求偏导数，而不需要显式知道。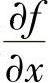

考察标量函数f（x），导数f′在x=a的值等于函数在f（a）处的斜率。对f（a）处斜率的一个合理近似是用附近的点a+h来计算一个“差分逼近”，如图3.9所示。

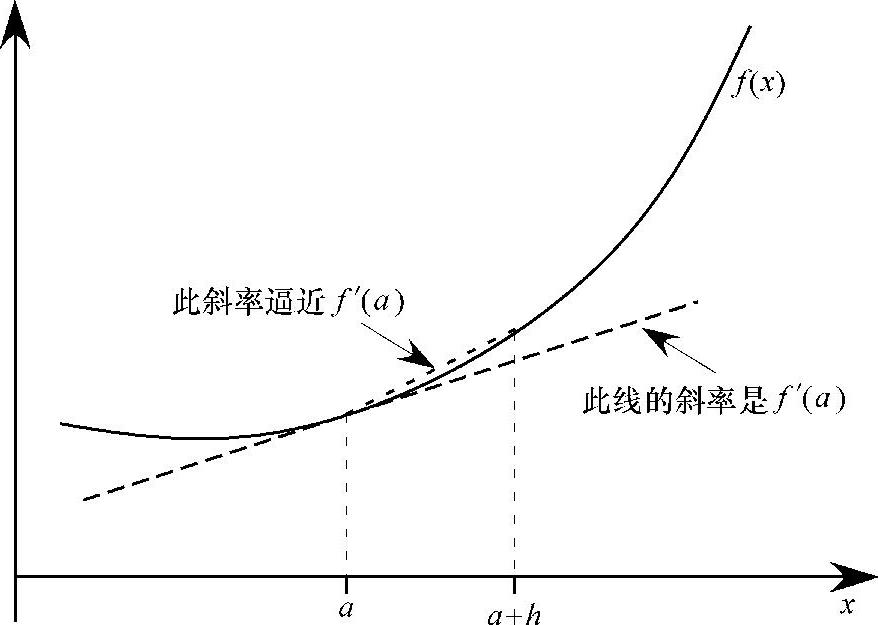
图3.9 差分逼近f（a）斜率的图形解释

这种做法具有数学上的依据，可以对f（a+h）进行Tay-lor级数展开导出：

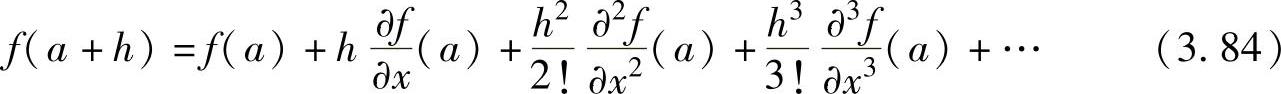
重新整理得

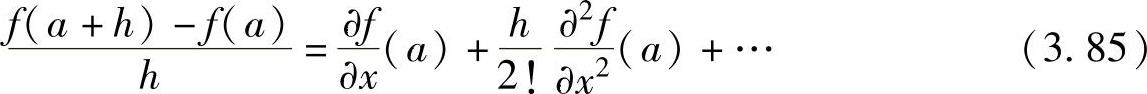
将高次项忽略得

这个近似在h变得越来越小时精度会越来越高（极限情况下h→0，它就是精确的）。这种近似方法是单边差分逼近，被称为对函数f导数的“向前差分”逼近。类似的做法可以在a-h处进行级数展开，并得到

这种近似被称为“向后差分”逼近

现在考察两种方法的结合：

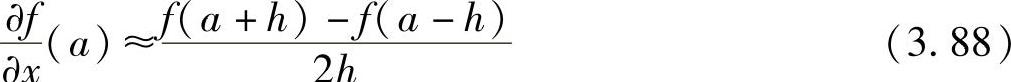
这种结合通常被称为“中心差分”逼近。其图形解释如图3.10所示。向前差分和向后差分逼近两者都具有O（h）数量级的误差，而中心差分逼近的误差数量级为O（h²），一般地会比向前差分和向后差分逼近具有更高的精度。

例3.8 考察多项式

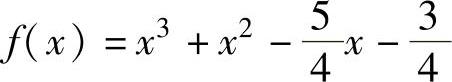
使用向前、向后和中心差分逼近求此多项式在[-2，1.5]区间的导数近似值，步长h=0.2。

解3.8 此函数的精确导数表达式为(www.xing528.com)

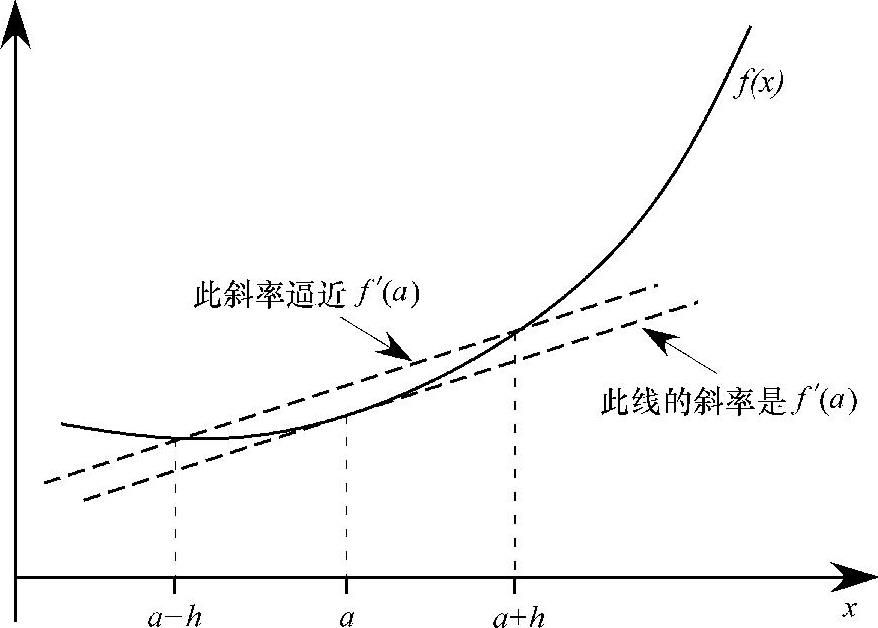
图3.10 中心差分逼近f（a）斜率的图形解释

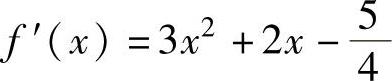
计算结果如下：

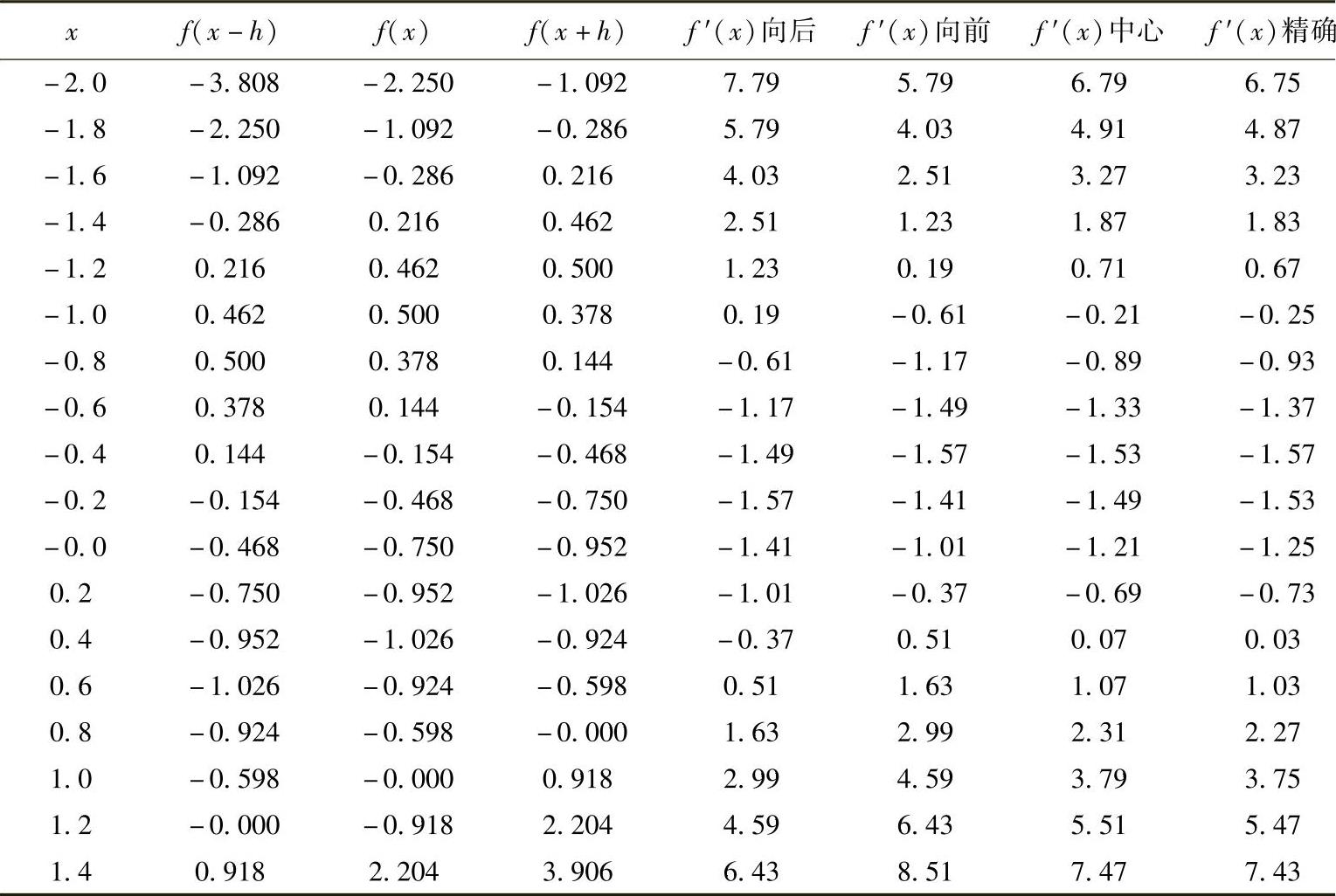
图3.11清楚地给出了不同导数近似方法的精确度。

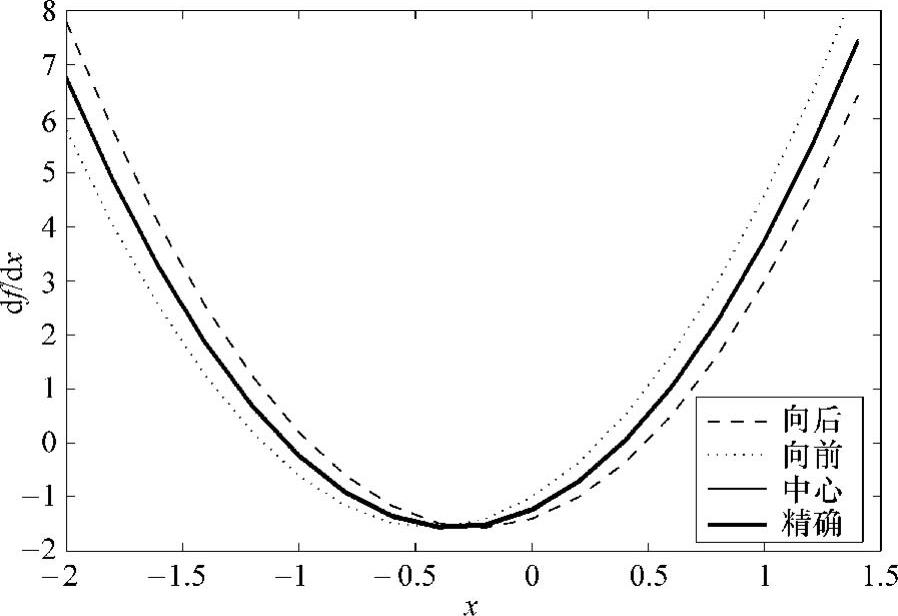
图3.11 精确与近似导数比较

通过继续应用Taylor级数展开方法并包括附加的信息，可以导出更高精度的近似式。一种广泛应用的此种近似式是Richardson近似：

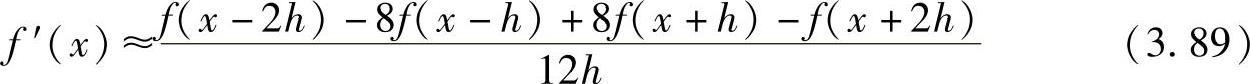
此近似式的误差数量级为O（h⁴）。

再次考察Newton-Raphson法，它需要计算Jacobi矩阵。上述近似方法可用来计算Jacobi矩阵中的偏导数，而不需要采用解析法进行直接计算。例如，考察如下的非线性方程组：

f₁（x₁，x2，…，x_n）=0

f₂（x₁，x2，…，xn）=0

︙

f_n（x₁，x₂，…，xn）=0

此方程组的Jacobi矩阵由形如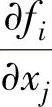的偏导数组成，此偏导数现在可以应用上述的任意一种近似方法进行计算。例如，采用中心差分法：

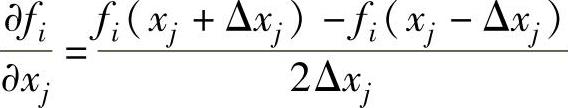
式中，Δx_j通常选择一个小增量（1%左右）。