Newton-Raphson迭代法优化算法

与上节描述的简单的不动点迭代法相比，存在多种迭代法具有更好的鲁棒收敛性。其中得到最广泛应用的迭代法是Newton-Raphson迭代法。这种方法的迭代格式也可以描述成：

I：x^k+1=g（x^k），k=1，…，∞但通常会比不动点迭代法具有更好的收敛性。

再次考察标量非线性方程

f（x^∗）=0 （3.20）

以Taylor级数展开的方式将此函数在点x^k展开，得到

如果假定当k→∞时迭代过程会收敛到x^∗，那么更新后的猜想值x^k+1可以用来替代x^∗，从而有

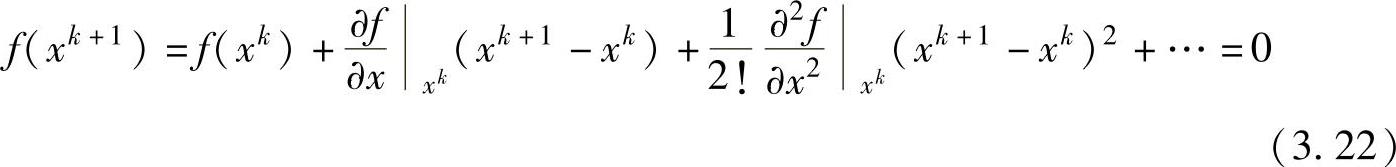
如果初始猜想值与x^∗“足够靠近”并位于x^∗的吸引域内，那么展开式的高次项可以被忽略，得到

直接求解x^k+1，将其表示为x^k的函数，可得到如下的迭代格式：

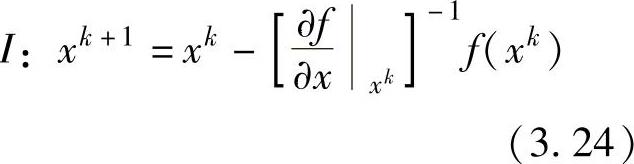
这就是著名的Newton-Raphson迭代法。

Newton-Raphson迭代法也有一个图形解释。考察例3.2中的同一个函数，将其画于图3.5中。在此方法中，当前迭代点处计算出的函数的斜率被用于产生下一个猜想值。对任意猜想值x^k，在函数上存在一个对应点f（x^k），其斜率为

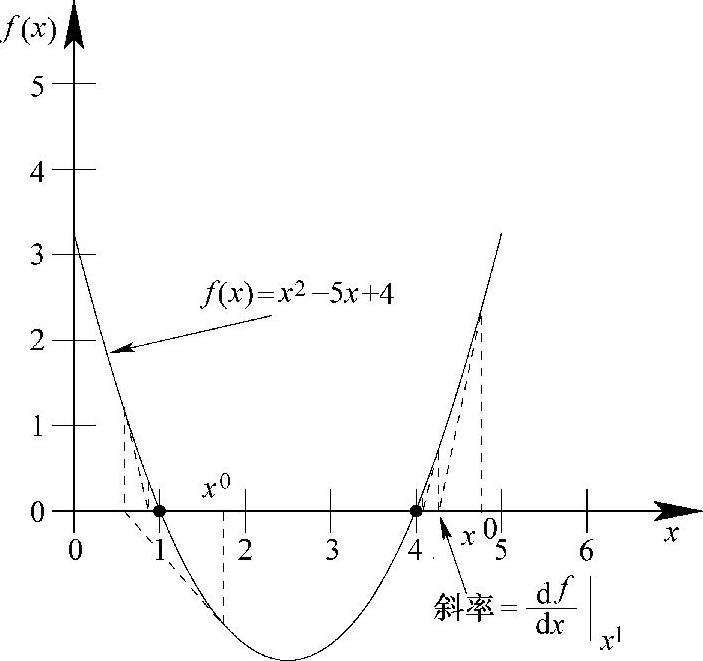
图3.5 Newton-Raphson法的图形解释(www.xing528.com)

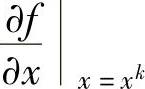
因此，下一个猜想值仅仅是据此斜率所作的直线与x轴的交点。这个过程不断重复直到所得到的猜想值足够靠近解x∗。一个迭代过程被认为已经收敛于x^k，如果

|f（x^k）|<ε

式中，ε是某个事先确定的容许误差。

例3.4 用Newton-Raphson法重新做例3.2。

解3.4 利用式（3.24）的Newton-Raphson迭代格式得到：

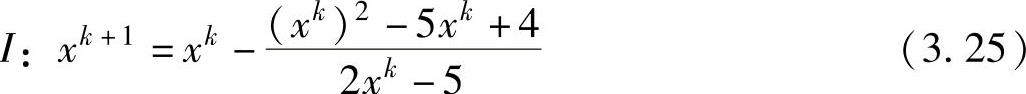
基于此迭代格式，从初始猜想值x⁰=3开始，得到的x^∗的估计值为

类似地，从初始猜想值x⁰=2开始，得到的x^∗的估计值为

在这个例子中，两个解都是Newton-Raphson迭代格式的吸引点。

但是，在某些情况下Newton-Raphson法将不能收敛。考察如图3.6所示的函数。图3.6a中，函数没有实根。图3.6b中，函数关于x^∗是对称的并且二阶导数等于零。图3.6c中，一个初始猜想值x⁰_a会收敛到解x_a^∗，一个初始猜想值x⁰_b会收敛到解x_b^∗；但是，另一个初始猜想值x⁰_c会使迭代锁定在虚线框内不断振荡，再也不能收敛到解。这张图支持如下的断言：如果初始值离真解太远，迭代将不会收敛；或者反过来说，初始值必须足够靠近真解，Newton-Raphson法迭代才能收敛。这一点也印证了在推导Newton-Raphson法时所做的初始假定：“如果迭代值足够靠近真解，Taylor级数展开式中的高次项可以忽略”。如果迭代值不是足够靠近真解，这些高次项是很大的，Newton-Raphson法所基于的假设条件就不再成立。

图3.6 Newton-Raphson法的收敛域