不动点迭代法及其收敛类型探讨

求解非线性方程组是一个复杂的问题，为了更好地理解大型方程组的机理，首先考虑一个一维的（即标量的）非线性方程是有启发意义的。该方程为

f（x）=0 （3.3）求解任何非线性方程的一种做法是试错法，大多数的理工科学生在其学习生涯中可能早已用过这种方法。

例3.1 求解如下方程的解

f（x）=x²-5x+4=0 （3.4）

解3.1 这是一个二次方程，其解可以用解析式表达。该方程的2个解为

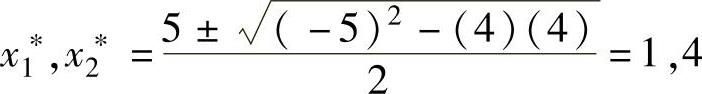
但是，如果解的解析式不存在的话，一种做法就是采用试错法。因为所求的解满足f（x）=0，因此可以通过监视f（x）的值来使真解x∗的估计值精确化。

通过注意函数的符号以及是否变号，可以逐次收缩解存在的区间。如果函数f（x）是连续的，并且f（a）·f（b）<0，那么在区间（a，b）内方程f（x）=0至少存在1个解。因为f（0.5）>0而f（1.5）<0，可以推出有一个解位于区间（0.5，1.5）内。

但是，根据f（x）符号的变化来寻找解的过程是冗长而乏味的，除了确定解的边界之外并不能指导如何确定下一个猜想值。一种更好的方法是根据前一次的猜想值构造一个不断更新的序列，可以定义一个迭代格式如下：

I：x^k+1=g（x^k），k=1，…，∞ （3.5）这种迭代被称为不动点迭代，因为在解上存在

x^∗=g（x^∗） （3.6）

例3.2 采用不动点迭代法求式（3.4）的解。

解3.2 式（3.4）可以被改写为

采用式（3.5）的符号，迭代格式变为

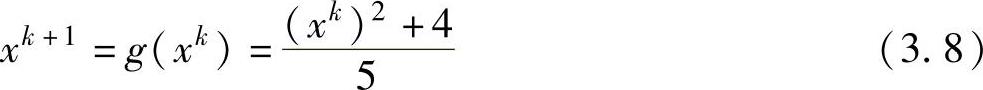
利用这个迭代格式，x^∗的估计值为

显然，这个序列将收敛于解x^∗=1。

现在考察同一个例子，但初始的猜想值不同，结果为

这种情况下，迭代值增加很快，不用几次迭代，其值就趋近于无穷大。因此，称这种情况为迭代“发散”。

这个例子引出了两个非常重要的问题：①迭代值序列是否会收敛？②如果收敛的话，将会收敛到什么解？为了回答这些问题，首先给出例3.2的图形解释。将式（3.7）两边的函数同时画出，得到如图3.1所示的一条曲线和一条直线。

这两条线的2个交点与原始方程f（x）=0的两个根相同。不动点迭代就是要寻找这个交点。考察图3.1中的初始猜想值x⁰，函数g（x）基于x⁰进行计算得到更新的迭代值x¹。这个过程在图形上的解释是，从x0点投射一条垂直线到g（x⁰），然后从g（x⁰）投射一条水平线到x¹。

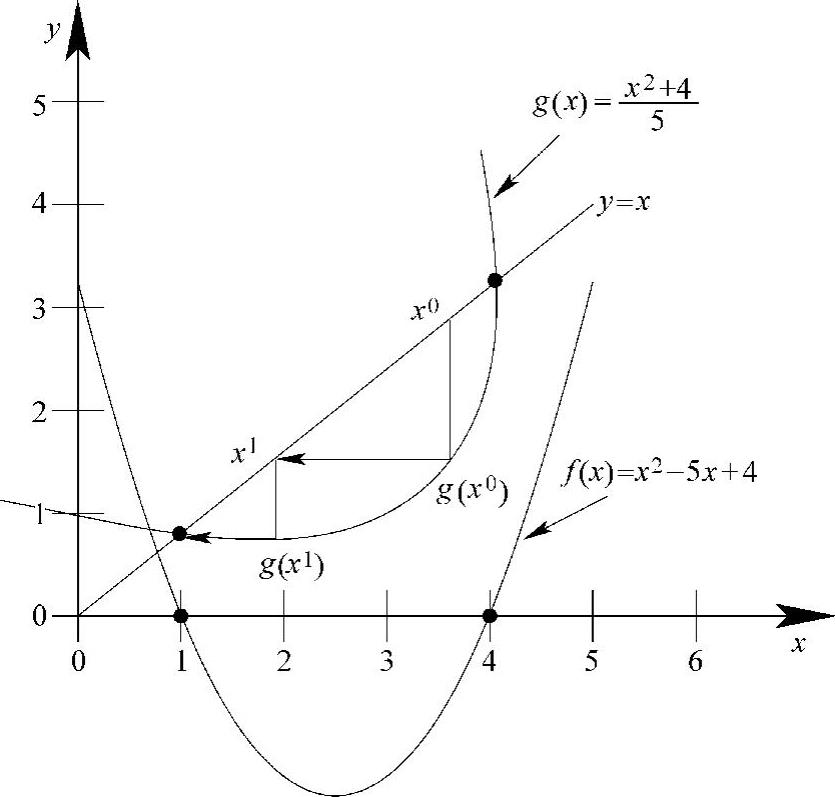
图3.1 不动点迭代的图形解释

g（x¹）的投射产生x²。类似的垂直和水平投射将最终直接到达两条线的交点。以这种方式，就能得到原始方程f（x）=0的解。

在本例中，解x^∗=1是不动点迭代的“吸引点”。点x^∗被称作迭代格式I的吸引点，指的是如果存在一个x^∗的开邻域S₀，使得对所有属于S₀（S₀∈S）的初始猜想值x⁰，其迭代值仍然属于S，并且

邻域S₀被称作x∗的“吸引域”[34]。这个概念可以用图3.2来进行说明，该图表明迭代格式I将收敛于x∗，只要x⁰足够靠近x∗。在例3.2中，不动点x∗=1是如下迭代格式的吸引点：

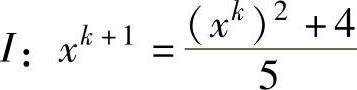
而x^∗=4则不是上述迭代格式的吸引点。x^∗=1的吸引域是位于区间-∞<x<4中的所有x。

事先确定某种迭代格式是否会收敛通常是困难的。在有些情况下，一系列的迭代值看起来会收敛，但即使迭代次数k→∞也不会趋近于x^∗。但是，存在几个定理，可以对迭代格式x=g（x）是否会收敛给出判断的依据。

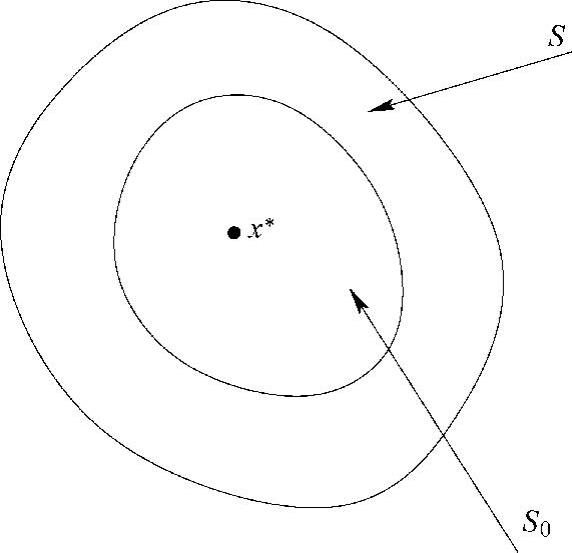
图3.2 x^∗的吸引域(www.xing528.com)

中值定理[47]：设函数g（x）及其导数g′（x）在区间a≤x≤b上都是连续的，那么至少存在一个ξ，a<ξ<b，使得

这个定理的意义如图3.3所示。如果函数g（x）定义在x=a和x=b之间的区间内，并且既是连续的又是可微（光滑）的，那么在点A和A′之间就可以画一条割线，这条割线的斜率是

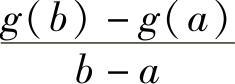
中值定理说的是在曲线上至少存在一个点x=ξ，该点上曲线的切线与割线AA′的斜率相同。

改写中值定理的公式为

g（b）-g（a）=g′（ξ）（b-a）

那么对于连续的两次迭代值x^k+1=b和x^k=a，有

g（x^k+1）-g（x^k）=g′（ξ^k）（x^k+1-x^k） （3.11）

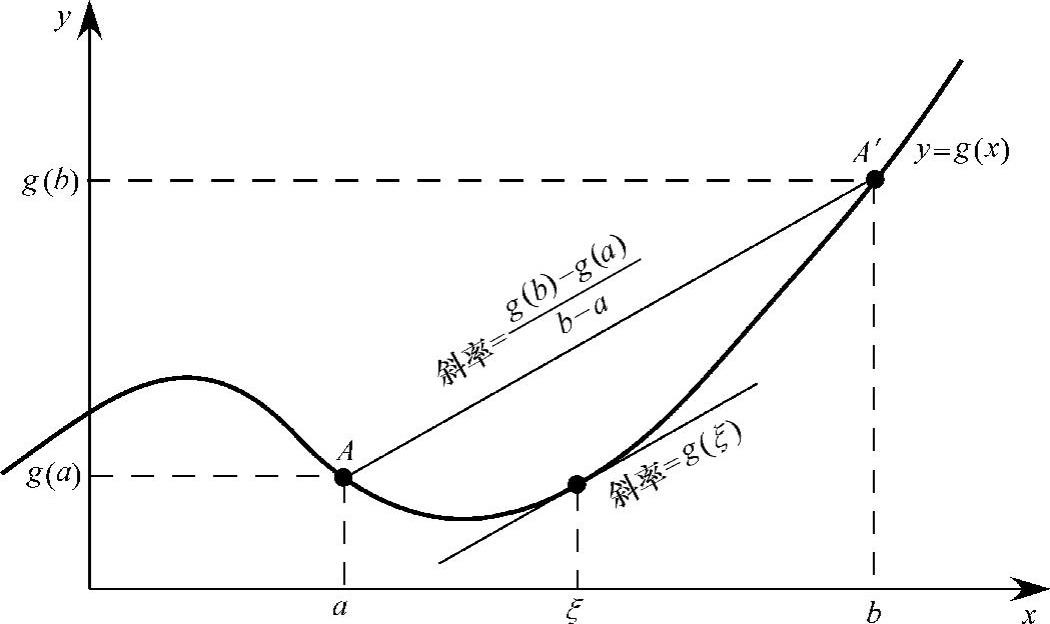
图3.3 中值定理的意义

或者取绝对值：

|g（x^k+1）-g（x^k）|=|g′（ξ^k）||（x^k+1-x^k）| （3.12）

只要采用合适的ξ^k，中值定理可以相继使用在每次迭代中。如果在包含x^∗和所有x^k的区间上导数g′（x）是有界的。即对于任意的k，

|g′（ξ^k）|≤M （3.13）

式中，M是正上限。那么，从初始猜想值x⁰开始，有

|x²-x¹|≤M|x¹-x⁰| （3.14）

|x³_-x2|≤M|x²-x¹| （3.15）

︙ （3.16）

|x^k+1_-xk|≤M|xk-x^k-1| （3.17）

将上面各式合并得到

|x^k+1_-xk|≤Mk|x¹_-x0| （3.18）

这样，对于任何的初始猜想值x⁰，只要

|g′（x）|≤M<1 （3.19）

那么，迭代就是收敛的。

另外一种类似但稍微有些不同的判断迭代过程是否收敛的定理是Ostrowski定理^[34]。该定理的表述为：如果迭代格式

I：x^k+1=g（x^k），k=1，…，∞

具有不动点x^∗，并且在x^∗点上是连续和可微的，那么如果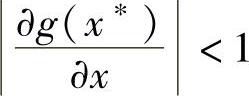，x∗就是I的吸引点。

例3.3 确定x^∗=1和x^∗=4是否为迭代格式（3.8）的吸引点。

解3.3 与式（3.8）对应的迭代格式I的导数为

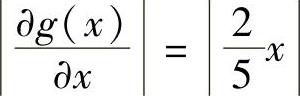
因此，对于x^∗=1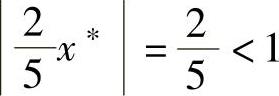，，因此x^∗=1是I的吸引点。而对于x^∗=4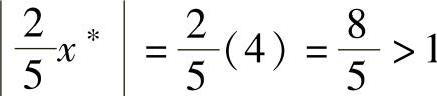，，因此x^∗=4不是I的吸引点。

对于不动点迭代，存在4种可能的收敛类型，如图3.4所示。图3.4a展示了g′（x）在0和1之间的情况，即使初始猜想值x⁰远离x^∗，相继的x^k的值也会从一侧趋近于解，这种情况被定义为“单调收敛”。图3.4b展示了g′（x）在-1和0之间的情况，即使初始猜想值x⁰远离x^∗，相继的x^k的值会首先从一侧然后从另一侧振荡地趋近于解，这种情况被定义为“振荡收敛”。图3.4c展示了g′（x）大于1的情况，此时会导致“单调发散”。图3.4d展示了g′（x）<-1和|g′（x）|>1的情况，此时会导致“振荡发散”。

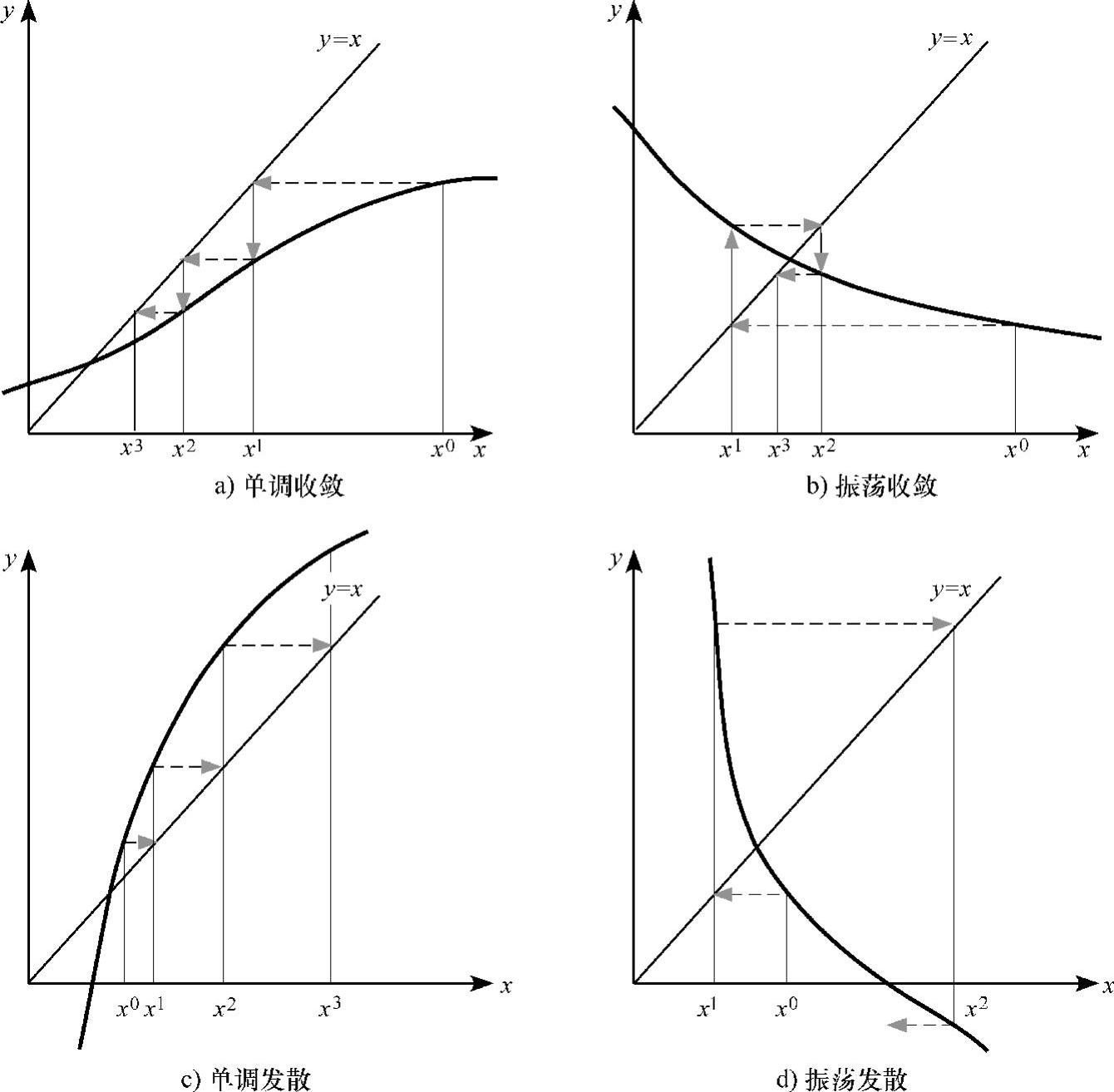
图3.4 迭代x=g（x）的4种可能收敛类型