【摘要】:很多系统可以被一般性地描述为F=0 (3.1)式中,x是一个n维向量,F是一个非线性映射,其源域和值域都在n维实线性空间Rn中。映射F也可以表述为一个n维的函数向量:式中至少有一个函数是非线性的,且每个函数不一定包含所有n个状态变量xi,但每个状态变量至少出现在其中的一个函数中。一般地,上述非线性方程组的解x无法用解析式来表达。但是,这些问题又是求解非线性方程组的核心问题,不能完全被忽略掉。
很多系统可以被一般性地描述为
F(x)=0 (3.1)
式中,x是一个n维向量,F是一个非线性映射,其源域和值域都在n维实线性空间Rn中。映射F也可以表述为一个n维的函数向量:
式中至少有一个函数是非线性的,且每个函数不一定包含所有n个状态变量xi,但每个状态变量至少出现在其中的一个函数中。一般地,上述非线性方程组的解x∗无法用解析式来表达。因此,非线性方程组通常用数值方法来求解。在很多情况下,通过不断地改进近似解,可以找到一个任意逼近其真实解x∗的近似解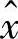 ,使得
,使得
此类方法通常是迭代性质的。所谓迭代解法是这样一种方法,采用一个初始的猜想解x0以构造出一个解的序列x0、x1、x2、…,而希望该序列能够任意逼近所期望的解x∗。
采用迭代法时存在三个主要的问题,即(https://www.xing528.com)
1)迭代过程的定义是否合适?即迭代过程能够执行下去而不发生数值计算上的困难。
2)迭代值(即更新值的序列)能否收敛到式(3.1)的一个解?该解是所期望的解吗?
3)整个求解过程的效率如何?
为了完全(或部分)回答这些问题,可以写好几本书,因此这些问题不可能在本章中进行完整的论述。但是,这些问题又是求解非线性方程组的核心问题,不能完全被忽略掉。因此本章将尽量提供足够的细节,以使读者理解不同种类的迭代方法的优点和缺点。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




