共轭梯度法求解例2.7中的系数问题

1.证明对于n×n方阵，其LU分解所需要的乘除法次数为n（n²-1）/3。

2.考察线性方程组Ax=b，其中

和

采用只有4位十进制数的精度，用LU分解法求解该方程组。

（a）不选主元

（b）部分选主元

如果有差别的话，对两者的差别进行评论。

3.证明如下矩阵不存在LU分解

4.假设A的LU分解是已知的，写一个算法求解方程x^TA=b^T。

5.对如下矩阵，求A=LU（不选主元）和PA=LU（部分选主元）

（a）

（b）

6.写一个基于LU分解的算法来求任意非奇异矩阵A的逆。

7.求解问题5（b）中的方程组，其中

（a）采用LU分解和前代/回代算法。

（b）采用Gauss-Jacobi迭代法，需要几次迭代？

（c）采用Gauss-Seidel迭代法，需要几次迭代？

（d）采用共轭梯度法，需要几次迭代？

（e）采用GMRES方法，需要几次迭代？

设初始解

迭代算法的收敛误差指标为10^-5。

8.应用Gauss-Seidel迭代于如下方程

设x⁰=[0.33116 0.70000]^T，并解释发生了什么。

9.采用共轭梯度法求解问题2中的方程。(www.xing528.com)

10.采用GMRES方法求解问题2中的方程。

11.考察如下的n×n三对角矩阵

式中，a是实数。

（a）验证T_a的特征值由下式给出

λ_j=a-2cos（jθ） j=1，…，n

式中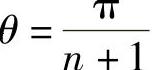

（b）令a=2

i.对这个矩阵，Jacobi迭代收敛吗？

ii.对这个矩阵，Gauss-Seidel迭代收敛吗？

12.求解Ax=b的共轭梯度法的另一种形式可以基于误差函数E_k（x^k）=<x^k-x，x^k-x>，其中<·>表示内积。其解为

x^k+1=xk+α_kσ_k

应用σ₁=-A^Tr₀和σ_k+1=-A^Tr_k+β_kσ_k，推导这种共轭梯度算法。系数α_k和β_k可以表示为

利用这种共轭梯度法求解例2.7。

13.写一个具有2个输入（A，flag）的子程序，对任意非奇异矩阵A，将输出（Q，P），使得

•flag=0，A=LU，P+I

•flag=1，PA=LU

其中

Q=L+U-I

14.对于如下的非奇异矩阵，采用问题13中的子程序，求出P和Q：

（a）

（b）

15.写一个具有2个输入（A，b）的子程序，对任意非奇异矩阵A，该子程序输出方程Ax=b的解x。采用前代和回代方法。此子程序应当与问题13中所开发的子程序合并。

16.采用问题13和问题15中的子程序，求解如下线性方程组