广义最小残差法在解空间中的应用

如果矩阵A既不是对称的，也不是正定的，那么就不能保证下式

<Aρ_k+1，Aσ_k+1>

为零，从而搜索向量不是相互正交的。为了构成解空间的基，相互正交是必须的。因此，这个基必须采用显式方法构造。共轭梯度方法的扩展，被称为广义最小残差法（GMRES），在如下向量张成的子空间中使残差的范数最小化：

r⁰，Ar⁰，A²r⁰，…，A^k-1r⁰

式中，向量r⁰是初始残差r⁰=‖b-Ax⁰‖，而解的第k次近似就是从这个空间中选择的。这个子空间是一个“Krylov子空间”，通过著名的Gram-Schmidt方法将其正交化；当应用于Krylov子空间时，这个正交化的过程被称为Arnoldi算法[37]。在第k步，GMRES方法将Arnoldi算法应用于构成第k个Krylov子空间的k个正交基向量上，以产生下一个基向量。Arnoldi算法将在7.3节更详细地描述。每步计算时，用矩阵A乘前面已求出的Arnoldi向量v_j，然后，将所得到的向量w_j对所有前面已求出的向量v_i正交化。列向量集V=[v₁，v₂，…，v_k]构成了Krylov子空间的正交基，而H是矩阵A在此子空间上的正交投影。

像Arnoldi算法那样的正交矩阵三角化需要确定一个n×n正交矩阵Q，使得

式中，R是一个m×m上三角矩阵。这样，求解过程就简化为求解三角矩阵方程Rx=Py，这里的P由Q的前m行组成。

为了将矩阵化为上三角矩阵，可以应用Givens旋转变换一次清除一个元素。Givens旋转变换是基于如下矩阵的变换：

式中，cs=cos（ϕ），sn=sin（ϕ），ϕ为经过适当选择的旋转角。采用Givens旋转变换可以将元素A_ki变为零。

GMRES方法的困难之一是随着k的增加，需要存储的向量个数增加，而乘法次数等于k²n/2（对于n×n矩阵）。为了克服这个困难，此算法可以按照迭代的方式应用，即可以每隔m步重启动一次，其中m是某个固定的整数。这种方法通常被称为GMRES（m）算法。

用于求解Ax=b的GMRES（m）算法

初始化：令k=0，并且

r₀=Ax⁰-b

e₁=[1 0 0 … 0]T

当‖r_k‖≥ε和k≤k_max时，设置

j=1

v₁=r/‖r‖

s=‖r‖e₁

cs=[0 0 0…0]^T

sn=[0 0 0…0]^T

当j<m时

（1）Arnoldi过程

（a）构成矩阵H，使得H（i，j）=（Av_j）T v_i，i=1，…，j

（b）令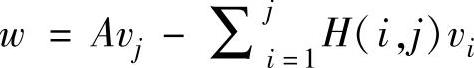

（c）令H（j+1，j）=‖w‖

（d）令v_j+1=w/‖w‖

（2）Givens旋转

（a）计算

（b）令

（c）求残差范数的近似值

α=cs（j）s（j）

s（j+1）=-sn（j）s（j）

s（j）=α

误差=|s（j+1）|

（d）令

H（j，j）=cs（j）H（j，j）+sn（j）H（j+1，j）

H（j+1，j）=0

（3）如果误差≤ε，则

（a）求解方程Hy=s，求出y

（b）作近似值更新

x=x-Vy

（c）此过程已收敛，返回。(www.xing528.com)

（4）令j=j+1

（5）如果j=m并且误差>ε（重新启动GMRES）

（a）令s=[100…0]

（b）解Hy=s求y

（c）计算x=x-Vy

（d）计算r=Ax-b

（e）令k=k+1

例2.9 采用GMRES方法重做例2.5。

解2.9 为了方便起见将例2.5重写如下：

求解方程

并且x⁰=[0000]^T，ε=10^-3

j=1 采用Arnoldi算法得到

应用Givens旋转变换得到

cs=[-0.5430 0 0 0]

sn=[0.8397 0 0 0]

s=[-2.9743 -4.5993 0 0]^T

由于误差（=|s（2）|=4.5993）大于ε，j=j+1再重复。

j=2 采用Arnoldi算法得到

应用Givens旋转变换得到

cs=[-0.5430 0.9229 0 0]

sn=[0.8397 0.3850 0 0]

s=[-2.9743 -4.2447 1.7708 0]^T

由于误差（=|s（3）|=1.7708）大于ε，j=j+1再重复。

j=3 采用Arnoldi算法得到

应用Givens旋转变换得到

cs=[-0.5430 0.9229 -0.9806 0]

sn=[0.8397 0.3850 0.1961 0]

s=[-2.9743 -4.2447 -1.7364 -0.3473]^T

由于误差（=|s（4）|=0.3473）大于ε，j=j+1再重复。

j=4 采用Arnoldi算法得到

应用Givens旋转变换得到

cs=[-0.5430 0.9229 -0.9806 1.0000]

sn=[0.8397 0.3850 0.1961 0.0000]

s=[-2.9743 -4.2447 -1.7364 -0.3473 0.0000]^T

由于误差（=|s（5）|=0），迭代已收敛。

根据Hy=s求解y，得

根据下式求x

x=x-Vy （2.90）

得

这与前面的例子结果一样。