共轭梯度法：一种高效求解线性方程组的迭代方法

另一种求解方程组Ax=b的常用迭代法是“共轭梯度”法。这种方法可以认为是对如下函数逐次沿射线方向进行最小化的方法。

E（x）=‖Ax-b‖² （2.57）

这种方法的一个有吸引力的特点是，如果矩阵A是正定的，那么可以保证至多在n步内收敛（忽略舍入误差）。如果矩阵A非常大且是稀疏的，共轭梯度法比Gauss消去法要常用得多，这种情况下可以在不到n步内得到解，特别是当矩阵A的性态很好时。如果矩阵A是病态的，那么舍入误差可能会导致n步迭代后仍然得不到足够精确的解。

在共轭梯度法中，每次迭代需要确定搜索方向ρ_k和参数α_k，以使函数f（x_k-α_kρ_k）沿着ρ_k方向最小化。一旦设定x^k+1等于x^k-α_kρ_k，新的搜索方向就确定了。随着共轭梯度迭代的进展，每个误差函数都与一个特定的射线即正交扩展相关。因此，共轭梯度法可简化为产生正交向量并寻找合适系数来表示所期望解的过程。共轭梯度法可以用图2.4来说明，设x∗表示精确解（但未知），x^k是一个近似解，而Δx^k=x^k-x^∗，给定任何搜索方向ρ_k，从此直线到x∗的最小距离可以通过构建垂直于此直线而连接x^∗的Δx^k+1来实现。由于精确解是未知的，因而构造的残差须与ρ_k垂直。不管新的搜索方向怎样选择，此残差的范数将不会增加。

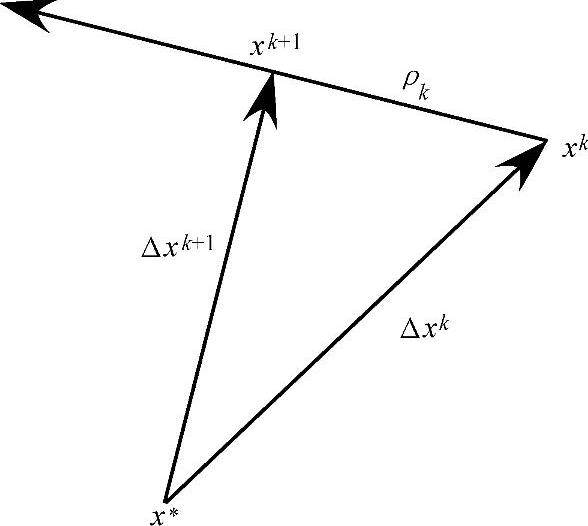
图2.4 共轭梯度法

所有求解Ax=b的迭代法都定义一个如下的迭代过程：

x^k+1=x^k+α_k+1ρ_k+1 （2.58）

式中，x^k+1是需要更新的值，α_k是步长，ρ_k定义一个在Rⁿ空间的方向，算法沿着此方向更新估计值。

设第k步的残差向量为

r_k=Ax^k-b（ 2.59）

而误差函数由下式给出：

E_k（x^k）=‖Ax^k-b‖² （2.60）

那么在k+1步使误差函数最小化的系数为

上式的几何解释是沿着ρ_k+1定义的射线方向使E_k+1最小化。更进一步，一种改进的算法是在由两个向量张成的平面内寻找E_k+1的最小值，即

x^k+1=x^k+α_k+1（ρ_k+1+β_k+1σ_k+1） （2.62）

式中，射线ρ_k+1和σ_k+1在Rⁿ空间张成一个平面。当所选择的向量正交，即满足

<Aρ_k+1，Aσ_k+1>=0 （2.63）

时，为了使误差函数E_k+1最小化而选择的方向向量和系数是最优的。式（2.63）中的<·>表示内积。满足式（2.63）正交条件的向量被称为关于算子A^TA相互共轭，其中A^T是A的共轭转置。选择合适向量的一种方法是选择σ_k+1与ρ_k正交，这样就不需要在每一步中确定两个正交向量。虽然这简化了迭代过程，但在产生向量ρ时存在隐性的递归依赖性。

求解Ax=b的共轭梯度算法

初始化：令k=0，和

r₀=Ax⁰-b （2.64）

ρ₀=-A^Tr₀ （2.65）

如果‖r_k‖≥ε，则

x^k+1=xk+α_k+1ρ_k （2.67）

r_k+1=Ax^k+1-b （2.68）

ρ_k+1=-A^Tr_k+1+B_k+1ρ_k （2.70）

k=k+1 （2.71）

对于任意的非奇异正定矩阵A，共轭梯度法至多在n步内得到解（忽略舍入误差）。这是由n个方向向量ρ₀、ρ₁、…必定会张成一个解空间而得出的直接结果。有限步终止是共轭梯度法相对于诸如松弛法等其他迭代法的一个巨大优势。(www.xing528.com)

例2.7 用共轭梯度法重新计算例2.5。

解2.7 为方便起见将例2.5的问题重写如下：

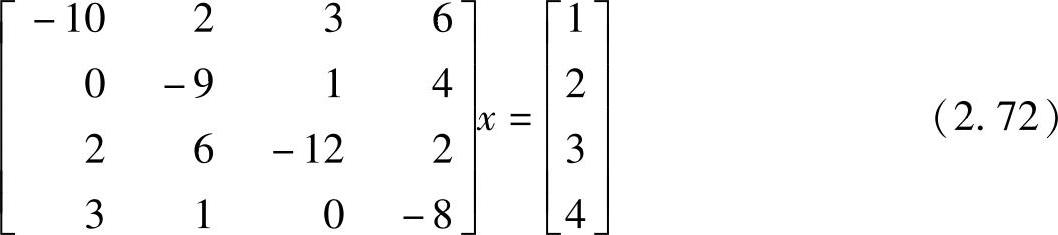
并且x⁰=[0000]^T

初始化：令k=1，并且

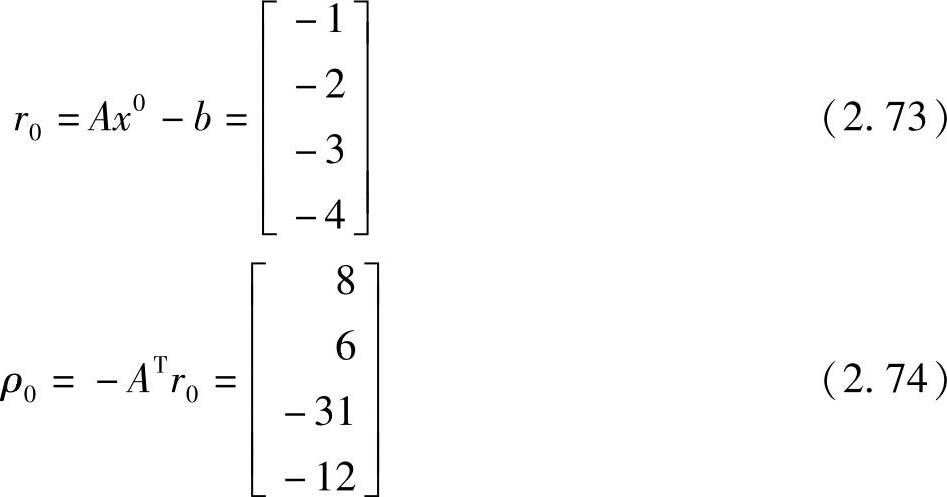
初始的误差为

E₀=‖r₀‖²=（5.4772）²=30 （2.75）

第1次迭代

对应的误差为

E₁=‖r₁‖²=（4.9134）²=24.1416 （2.81）类似地，第2～4次迭代如下：

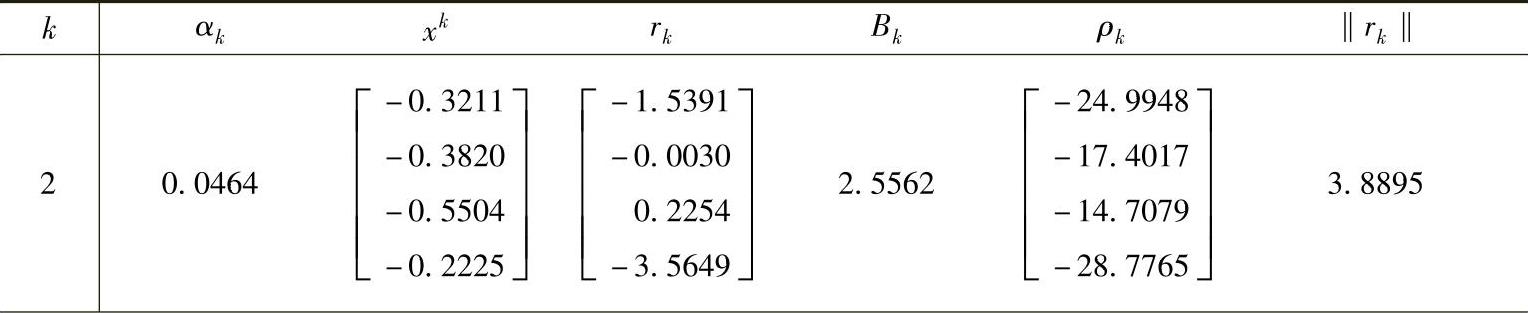
（续）

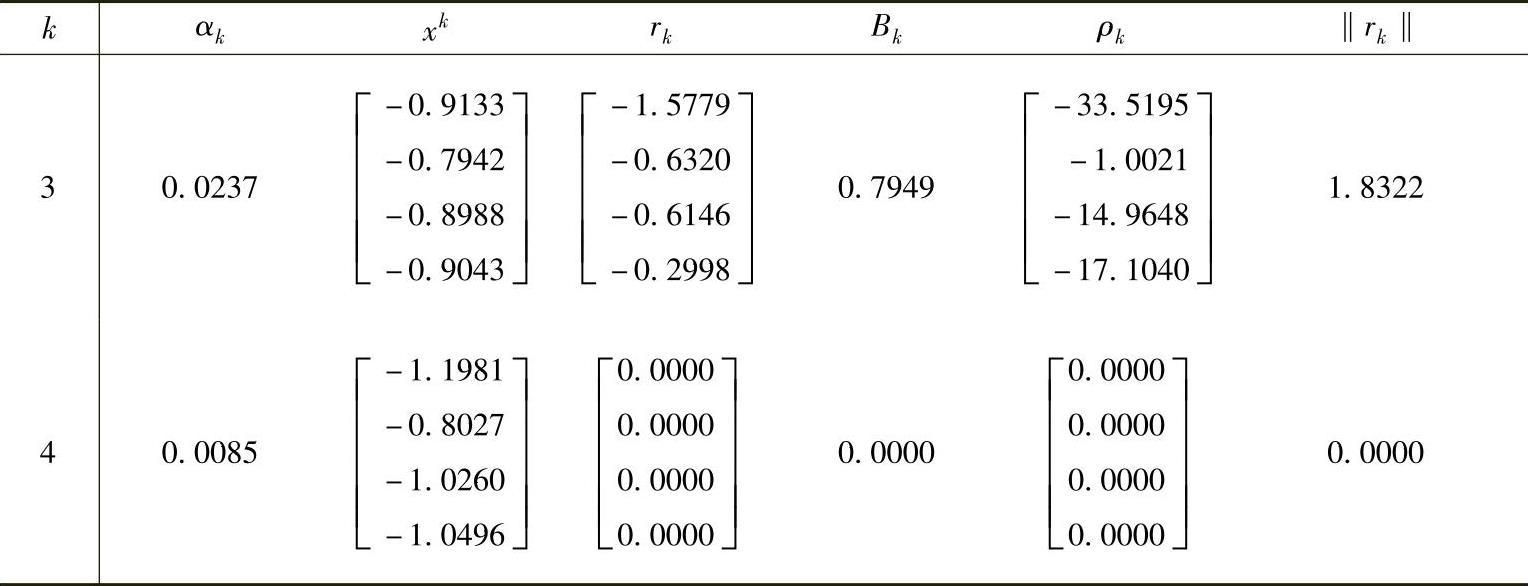
正如该算法所保证的，迭代在第4步收敛。

不幸的是，对于一般性的线性方程组，共轭梯度法所需要的乘除法次数大大超过LU分解法。共轭梯度法在如下两种情况下更有竞争力：第1种情况是矩阵非常大并且很稀疏；第2种情况是矩阵具有特殊结构，LU分解不容易处理。在有些情况下，共轭梯度法的收敛速度可以通过“预处理”而得到改进。

正如在Gauss-Seidel和Jacobi迭代中所看到的，迭代算法的收敛速度与迭代矩阵的特征值频谱紧密相关。因此，采用重新定标或矩阵变换的方法将原始方程组变换成具有更好矩阵特征值频谱的方程组，将能够大大提高收敛的速度。这个过程被称为预处理。已开发出了针对稀疏矩阵的多个系统性的预处理方法，其中最基本的做法是将方程组

Ax=b

变换成等价的方程组

M^-1Ax=M^-1b

式中，M^-1用来近似A^-1。例如，此种方法可用于非完整的LU分解，即使用LU分解但所有的填入被忽略。如果矩阵A是对角占优的，M^-1的一个简单近似是

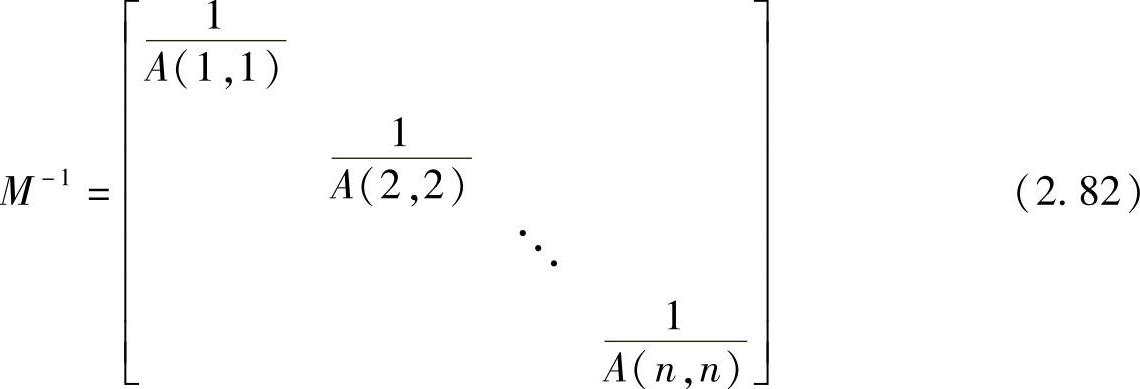
这种预处理策略将线性方程组重新定标，使得对角线上的元素全部相等。这种处理可以补偿元素大小上的数量级的差别。注意，重新定标对矩阵固有的病态特性并没有任何作用。

例2.8 采用预处理的方法重做例2.7。

解2.8 设M^-1采用式（2.82）的形式，因此有

求解A′x=b′，采用共轭梯度法得到如下的误差序列：

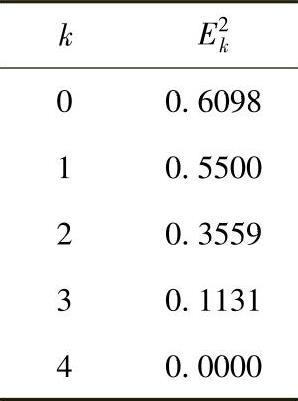
虽然也要用4步迭代才收敛，但注意在k<4时，其误差与例2.7的情况相比要小很多。对于大型线性方程组，可以想象误差将会足够快速地下降，以至于在第n步迭代之前就可以终止。如果只需要x的一个近似解，这种方法也是很有用的。