Jacobi松弛法和Gauss-Seidel松弛法的收敛条件

松弛法本质上是迭代法，它产生一系列向量，理想条件下会收敛于解x∗=A^-1b。松弛法可以以多种方式应用于求解式（2.1）。在所有情况下，采用松弛法的一个主要优势来自于不需要对一个大型线性方程组进行直接求解，并且可以有效地利用该方程组的一些潜在特性（这些特性目前是相对不变的）。此外，随着并行处理技术的出现，松弛法比直接法更容易实现并行计算。最常用的两种松弛法是Jacobi法和Gauss-Seidel法^[56]。

这些松弛法可以应用于求解线性方程组：

Ax=b （2.43）

松弛法的一种通用做法是定义一个“分裂矩阵”M，使得式（2.43）可以重写成如下的等价形式：

Mx=（M-A）x+b （2.44）这种分裂方法可以导出如下的迭代过程：

Mx^k+1=（M-A）x^k+bk=1，…，∞ （2.45）式中，k是迭代指标。对于一个初始的猜想值x⁰，此迭代过程产生一系列向量x¹、x²、…。通过选择不同的矩阵M，可以导出不同的迭代方法。松弛法的目标是选择一个分裂矩阵M使得上述向量序列容易计算，并且能够快速收敛到解。

设A被分裂成L+D+U，其中L是严格下三角矩阵，D是对角矩阵，而U是严格上三角矩阵。注意，这些矩阵是不同于LU分解时所得到的L和U的。那么采用Jacobi松弛法求解向量x的迭代式为

x^k+1=-D^-1（（L+U）x^k-b） （2.46）

或等价地写成标量形式：

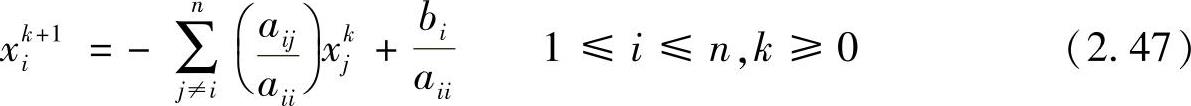
在Jacobi松弛法中，向量x^k+1所有元素的更新只用向量x^k的元素。因此这种方法有时也称为同时替换法。

Gauss-Seidel松弛法是类似的：

x^k+1=-（L+D）-1（Ux^k-b） （2.48）

或用标量形式：

Gauss-Seidel法的优势是每个新的更新x^k+1_i仅依赖于前面迭代已计算得到的值x^k+1₁、x₂^k+1、…、x^k+1_i-1。由于状态是一个接一个被更新的，新数值可以存储在老数值所占的位置上，从而减小了存储的需求。

由于松弛法是迭代的，确定在什么条件下能保证收敛到如下的精确解是必须的：

x^∗=A^-1b （2.50）

众所周知，对于任意的初始猜想值x⁰，Jacobi松弛法收敛的充分必要条件是如下矩阵的所有特征值落在复平面的单位圆内^[56]。

M_J≜-D^-1（L+U） （2.51）

类似地，对于Gauss-Seidel松弛法，相应的收敛条件是如下矩阵的所有特征值落在复平面的单位圆内。

M_GS≜-（L+D）-1U （2.52）

实际上，这些条件是难以确认的。但存在几个容易确认的更一般性的条件，可以保证收敛。特别地，如果A是严格对角占优的，那么不管是Jacobi松弛法还是Gauss-Seidel松弛法，都能保证收敛到精确解。

初始向量x⁰可以是任意的，但是，如果存在解的更好的猜想值，就应该使用之，这样能够更快速地收敛到指定精度下的精确解。

一般地对大多数问题，Gauss-Seidel法比Jacobi法收敛速度快。如果A是一个下三角矩阵，Gauss-Seidel法可以通过1次迭代收敛到精确解，而Jacobi法则需要n次迭代才能收敛到精确解。但Jacobi法也有其优点，即每次迭代计算时，x^k+1_i是独立于所有其他的x_j^k+1（j≠i）的；这样，所有x^k+1_i的计算可以并行处理。因此，这种方法非常适合于并行处理^[36]。

不管是Jacobi法还是Gauss-Seidel法，都可以被一般化为分块Jacobi法和分块Gauss-Seidel法。即A被分裂成分块矩阵L+D+U，其中，D是分块对角矩阵，L和U分别是分块下三角矩阵和分块上三角矩阵。分块情况与标量情况相同，也存在收敛的充分必要条件，即M_J和M_GS的特征值必须落在复平面的单位圆内。

例2.5 采用（1）Gauss-Seidel法和（2）Jacobi法求解如下方程。(www.xing528.com)

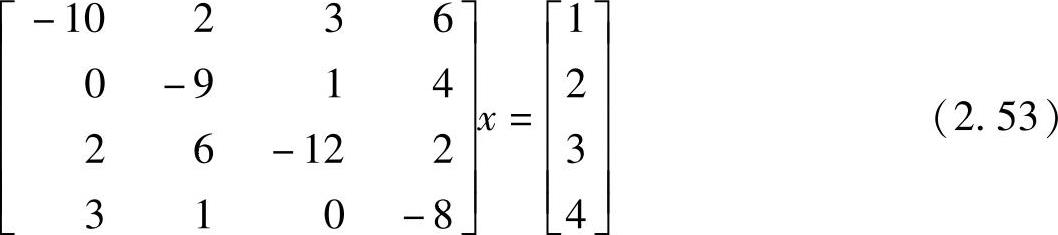
解2.5 采用由式（2.49）给出的Gauss-Seidel法，当初始向量x=[0000]^T时得到如下的迭代序列：

Gauss-Seidel法已收敛到解

x=[-1.1980 -0.8027 -1.0259 -1.0496]^T

采用由式（2.47）给出的Jacobi法，当初始向量x=[0000]^T时得到如下的迭代序列：

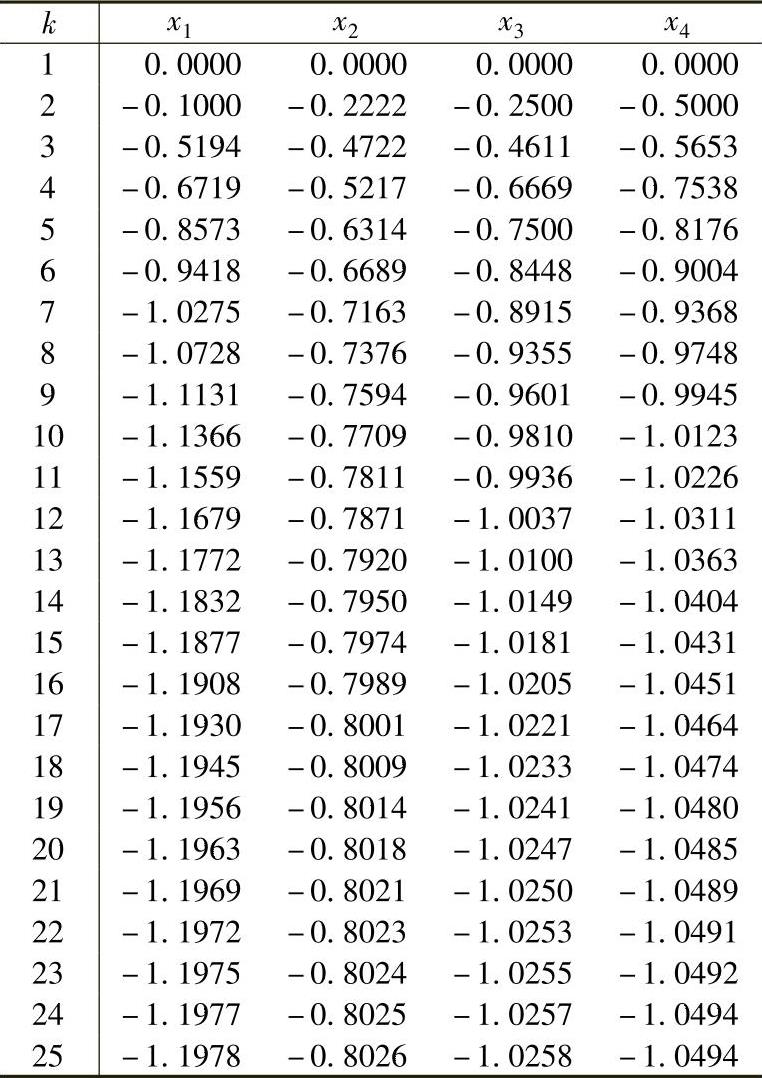
Jacobi法所收敛到的解与Gauss-Seidel法相同。迭代过程中的误差如图2.3所示，该图采用半对数刻度，而误差定义为（x^k_i-x_i^∗）（i=1，…，4）的最大值。Gauss-Seidel法和Jacobi法都呈现出线性收敛特性，但Gauss-Seidel法的斜率更陡，因而在相同的初始值下能更快地收敛到误差限内。

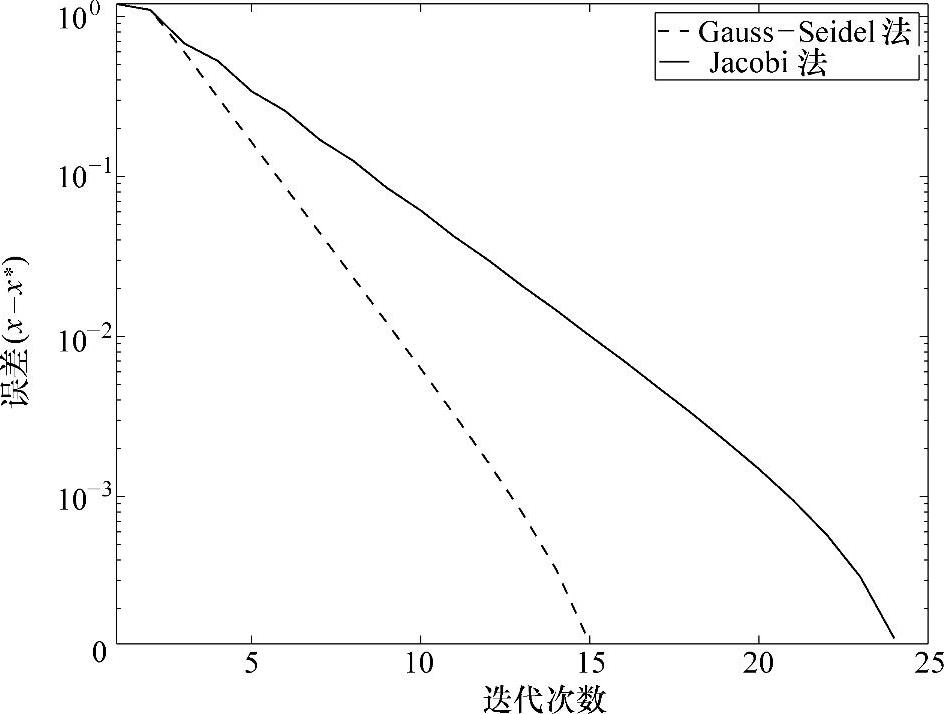
图2.3 Gauss-Seidel法和Jacobi法的收敛速度

例2.6 采用Jacobi迭代法重做例2.2。

解2.6 再次采用例2.5中的迭代过程，得到如下的Jacobi迭代序列：

显然，上述迭代序列是不收敛的。为了理解为什么它们是发散的，考察Ja-cobi迭代矩阵：

M_J的特征值为

都大于1并落在单位圆外。因此，不管取什么初始值，Jacobi法都不能收敛，因而不能用来求解例2.2的方程组。

如果迭代矩阵M_J和M_GS的最大特征值小于1但几乎等于1，那么收敛过程将非常慢。这种情况下，希望引入一个加权因子ω来改善收敛的速度。根据

x^k+1=-（L+D）^-1（Ux^k-b） （2.54）

得到

x^k+1=x^k-D^-1（Lx^k+1+（D+U）x^k-b） （2.55）

带有加权因子ω的一种新的迭代方法为

x^k+1=x^k-ωD^-1（Lx^k+1+（D+U）x^k-b） （2.56）

这种方法被称为“逐次超松弛（SOR）”法，其中松弛系数ω>0。注意，如果松弛迭代收敛，它们会收敛到解x^∗=A^-1b。SOR法收敛的一个必要条件是0<ω<2^[27]。除了很少的简单情况外，计算ω的最优值是困难的。通常通过试错的方法确定最优值，但是分析表明，对于n>30的线性方程组，最优的SOR方法可以比Jacobi方法快40倍^[27]。随着n的增大，对收敛速度的改进将更加明显。