条件数和误差传播

Gauss消去法和LU分解法被认为是直接法，因为它们通过有限步就能够计算出解向量x^∗=A^-1b，并不需要迭代过程。在具有无限精度的计算机上，直接法会得出精确解x^∗。但是，由于计算机是有限精度的，因而所获得的解也只有有限精度。矩阵的“条件数”是一种用来衡量解的精确程度的有用指标。矩阵A的条件数一般定义为

式中，λ_max和λ_min表示矩阵A^TA的最大和最小特征值。不管矩阵A本身的特征值是实数还是复数，A^TA的特征值是实数并且非负。

矩阵的条件数是该矩阵特征向量线性独立性的一种度量。奇异矩阵至少有一个零特征值，并且包含至少一个退化行（即该行可以通过其他行的线性组合来表示）。单位矩阵的所有特征值为1，其特征向量是最线性独立的，它的条件数为1。如果一个矩阵的条件数大大超过1，那么就称该矩阵是“病态的”。条件数越大，求解过程相对于A的元素的微小变化就越敏感，解向量包含数值误差的可能性就越大。

由于在求解过程中引入的数值误差，计算得到的式（2.1）的解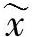将不同于其精确解x^∗，设两者存在的误差为Δx。其他误差，如近似误差、测量误差和舍入误差等，也会引入到矩阵A和向量b中。Gauss消去法产生的解大致具有下式描述的十进制正确位数：(www.xing528.com)

tlog₁₀β-log₁₀κ（A） （2.42）

式中，t是尾数的位长（对于典型的32位二进制字，t=24），β是基（对二进制运算，β=2），而κ是矩阵A的条件数。式（2.42）的一种解释是，在Gauss消去过程（因此也是LU分解过程）中，方程的解将会损失大约log₁₀κ的精确位数。基于矩阵元素的已知精度、条件数和机器精度，可以对数值解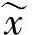的精度做出预测^[35]。