部分选主元的LU分解方法的优化标题

上述的LU分解过程假定了对角元是非零的。实际上不但要求对角元是非零的，还要求对角元与其他非零元具有相同的数量级。考察如下线性方程组的解：

通过观察，很容易得出此线性方程组的解为

x₁≈2

x₂≈1

而A的LU分解因子为

采用前代方法求解哑向量y得到：

y₁=1010

采用回代方法求解Uy=x得到

x₂=y₂≈1

x₁=10¹⁰-10¹⁰x₂≈0

这里，x₂的解是正确的，而x₁的解是完全不对的。为什么会发生这种情况呢？问题是式（2.30）中的10^-10对大多数计算机来说是太接近于零了。但是，如果将式（2.30）进行整理，变为

然后，再进行LU分解，则得到

哑向量y变为

通过回代，得到x为

x₂≈1

这与通过观察得到的解相同。因此，即使对角元不是精确等于零，将方程组的次序进行重新排列以使最大数值的元素位于对角元上，仍然是一种好的做法。这种做法被称为“选主元”，并导致了式（2.18）中的置换矩阵P。

由于Crout算法从第1列和第1行开始逐列和逐行计算矩阵Q，因此只能实施“部分选主元”，也就是只有Q（对应地A）的行可以相互交换，而列必须保持不变。为了选择最好的主元，需要在第j个对角元（在LU分解的第j步）下面的列元素中选择绝对值最大的元素，然后将该元素所在行与第j行相互交换。上述选主元策略可以简洁地表述为

部分选主元策略

（1）在LU分解的第j步，选择第k行作为交换行，k的选择满足如下条件：

|q_jj|=max|q_kj| 对k=j，…，n （2.32）

（2）将第j行与第k行进行交换，同时更新A、P和Q。

(www.xing528.com)

图2.2 初等置换矩阵P^j，k

置换矩阵P是由0和1构成的矩阵，它等于一系列初等置换矩阵P^j，k的乘积，这里P^j，k表示第j行与第k行相交换的初等置换矩阵。初等置换矩阵P^j，k如图2.2所示，它由单位矩阵通过交换第j行和第k行得到。通过左乘合适的P^j，k就能实现选主元的目的。因为这仅仅是行的交换，未知向量中的元素次序没有变化。

例2.4 采用部分选主元方法重做例2.3。

解2.4 为方便起见将A重写如下：

对于j=1，Q的第1列就是A的第1列，利用式（2.32）的选主元策略，第1列中q₄₁的绝对值最大，因此将第4行和第1行交换。对应的初等置换矩阵P^1，4为

对应的矩阵A变为

而j=1时的矩阵Q为

当j=2时，计算Q第2列得到的结果是

对第j列主对角元下面的元素进行最大值搜索，第j列（这里为第2列）的第4行元素绝对值最大，因此第2行与第4行交换，产生的初等置换矩阵P^2，4为

类似地，更新后的A为

而产生的矩阵Q为

当j=3时，计算Q第3列得到的结果是

这种情况下，主对角元具有最大的绝对值，因此不用再选主元。继续计算Q的第3行得到

最后，计算q₄₄得到最终的矩阵Q为

置换矩阵P等于上述2个初等置换矩阵的乘积：

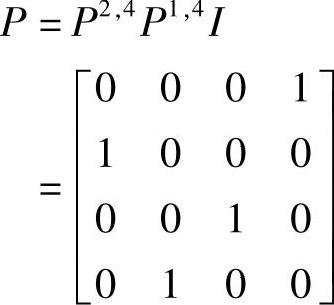
上述结果可以通过检查PA=LU而得到验证。而前代和回代计算将对修正过的向量b′=Pb进行。