采用LU分解和前代/回代算法求解方程组

Gauss消去法的向前消去过程产生了一系列与矩阵A相关的上三角矩阵和下三角矩阵，如式（2.9）所示。其中，矩阵W是一个下三角矩阵，而矩阵U是一个对角元为1的上三角矩阵。考虑到下三角矩阵的逆仍然是一个下三角矩阵，因此如果定义

L=≜W^-1

那么

A=LU

正是基于矩阵L和矩阵U，将矩阵的因子分解或消去算法命名为矩阵的“LU分解”。事实上，对于任何非奇异的矩阵A，存在一些置换矩阵P（有可能P=I），使得

LU=PA （2.18）

式中，U是对角元为1的上三角矩阵，L是对角元为非零的下三角矩阵，而P是由单位矩阵I通过行交换或列交换而形成的元素仅为0或1的矩阵。一旦选定一个合适的矩阵P，那么上述的LU分解就是唯一的[6]。如果P、L和U已经确定，那么方程组

Ax=b （2.19）

就可以迅速得到求解。在式（2.19）两边同时左乘矩阵P得

PAx=Pb=b′ （2.20）

LUx=b′ （2.21）

式中，b′仅仅是对向量b的一个重新排列。如果引入一个“哑”向量y，使得

Ux=y （2.22）

那么

Ly=b′ （2.23）

考虑到式（2.23）的结构为

向量y的元素可以通过直接代换得到：

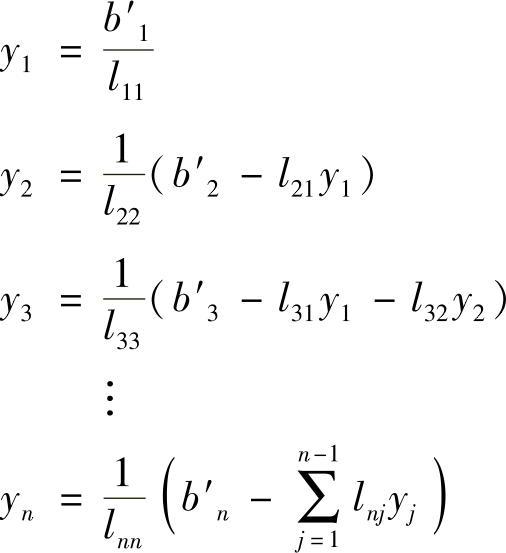
求出y以后，x就可以很容易根据如下方程求得：

类似地，解向量x可以通过回代得到：

x_n=y_n

x_n-1=y_n-1-u_n-1，nx_n

x_n-2=y_n-2-u_n-2，nx_n-u_n-2，n-1x_n-1

︙

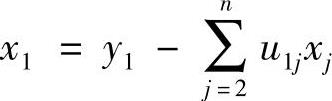
LU分解的价值在于，一旦矩阵A被分解成上三角矩阵和下三角矩阵，那么寻找解向量x就是一件直截了当的事了。注意上述求解过程并没有显式地对矩阵A求逆。

存在多种方法对矩阵进行LU因子分解，每种方法具有各自的优缺点。一种常用的LU分解方法被称为Croutb算法[6]。定义矩阵Q为

Crout算法逐列逐行地计算Q的元素，首先计算Q的列元素，然后计算Q的行元素，如图2.1所示。Q中的每个元素q_ij只依赖于A的元素a_ij和前面已经计算得到的Q的元素。

对矩阵A进行LU分解的Crout算法

（1）对矩阵Q进行初始化，即清零，并令j=1；

（2）根据下式计算Q的第j列（即矩阵L的第j列）：

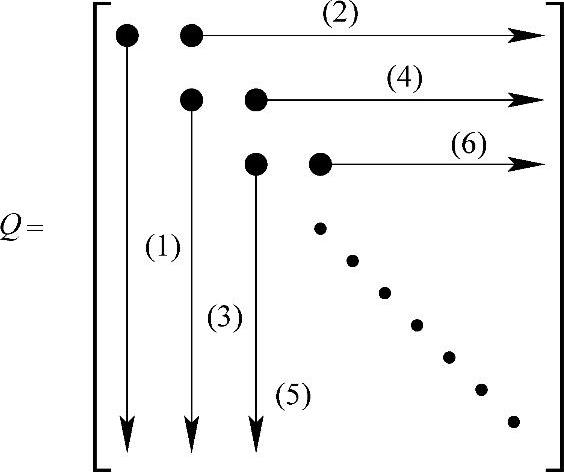
图2.1 矩阵Q列和行元素的计算次序

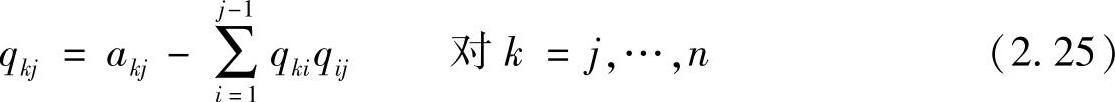
（3）如果j=n，则停止；

（4）假定q_jj≠0，根据下式计算Q的第j行（即矩阵U的第j行）：

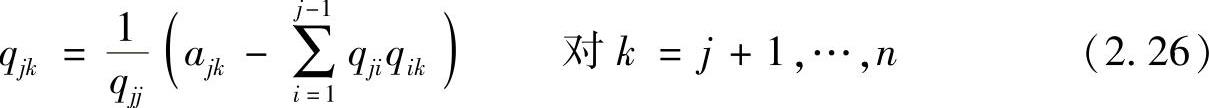
（5）令j=j+1，转到步骤（2）。

一旦完成LU分解，通过“前代”就能得到哑向量y：

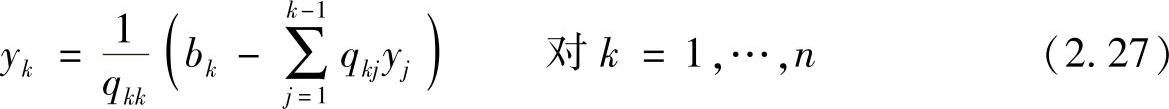
类似地，通过“回代”就能得到解向量x：

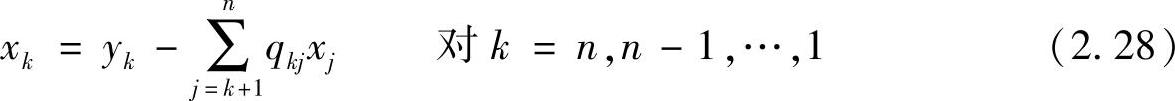
衡量LU分解过程计算量的一种指标是，获得解向量所需要的乘法和除法运算次数，因为两者都是浮点数运算。计算Q的第j列（L的第j列）需要的乘法和除法次数为

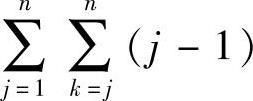(www.xing528.com)

类似地，计算Q的第j行（U的第j行）需要的乘法和除法次数为

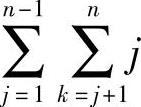
前代所需要的乘法和除法次数为

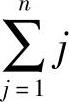
回代所需要的乘法和除法次数为

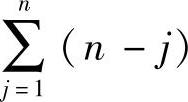
这样，可以算出LU分解所需要的乘法和除法次数为

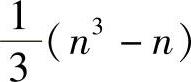
而前代和回代所需要的乘法和除法次数为n²。因此，求解式（2.1）线性方程组所需要的总的乘法和除法次数为

将这个乘除法次数与采用Cramer法则所需要的2（n+1）！次乘除法相比，对于任何较大阶数的矩阵，显然采用LU分解和前代/回代方法的计算效率要高得多。

例2.3 采用LU分解和前代/回代算法，求解例2.2中方程的解。

解2.3 第1步是求矩阵A的LU因子：

从j=1开始，式（2.25）表示Q的第1列与A的第1列完全相同。类似地，根据式（2.26），Q的第1行变为

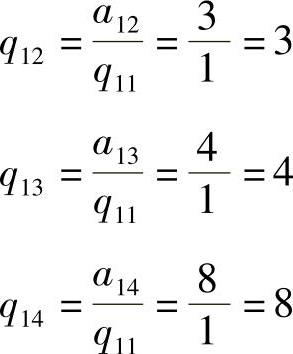
这样，对于j=1，矩阵Q变为

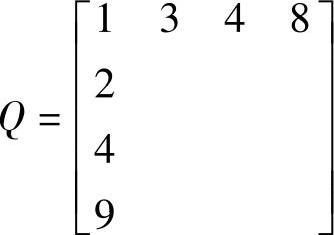
对于j=2，将分别计算矩阵Q主对角元下面的列元素和右面的行元素。对于Q的第2列有

q₂₂=q₂₂-q₂₁q₁₂=1-（2）（3）=-5

q₃₂=a₃₂-q₃₁q₁₂=3-（4）（3）=-9

q₄₂=a₄₂-q₄₁q₁₂=2-（9）（3）=-25

Q中的每个元素通过A中的对应元素和Q中已经求得的元素得到。注意乘积的第2个下标总是相同的，而第1个下标与正要计算的元素下标相同。这个规则对于列计算和行计算都是成立的。Q的第2行计算如下：

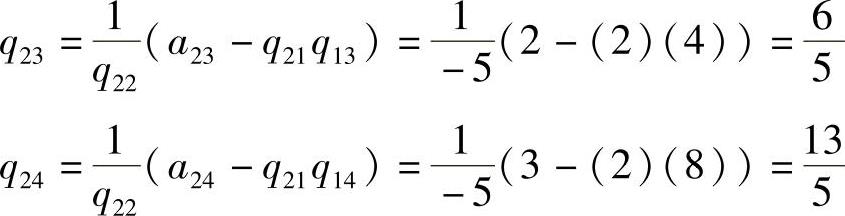
对j=2处理完以后，矩阵Q变为

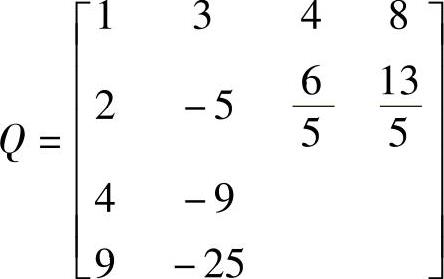
继续计算j=3，Q的第3列计算如下：

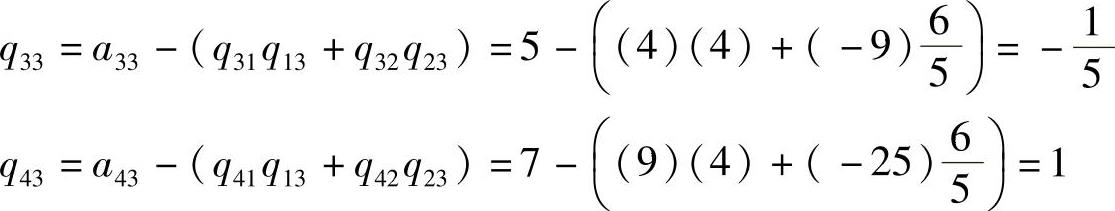
而Q的第3行变为

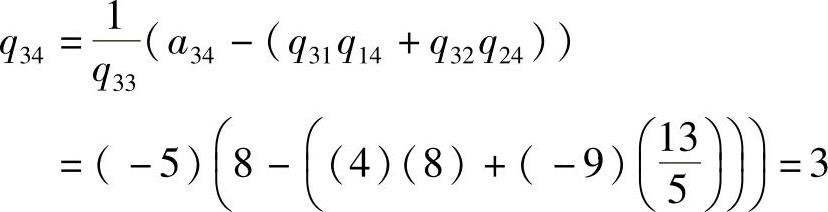
得到

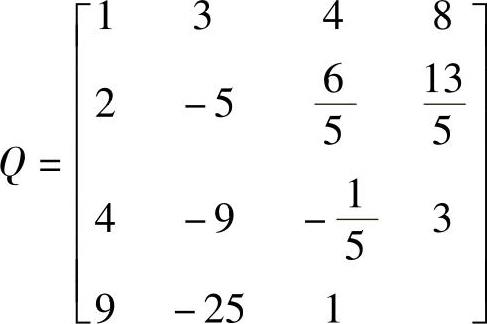
最后，计算j=4，最后一个对角元为

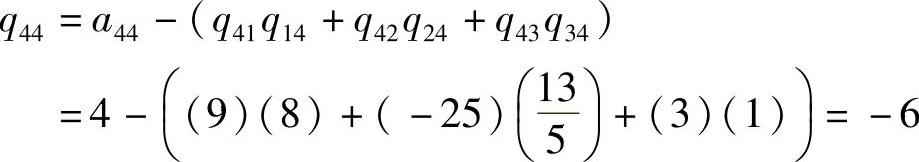
这样，

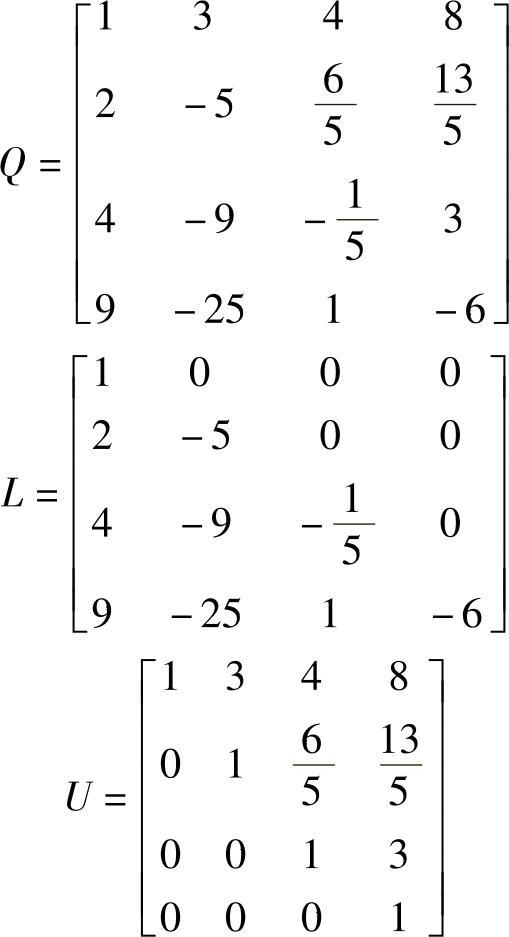
检查上述计算是否正确的一种方法是验证LU是否等于A，对于本例，结果是成立的。

一旦求得了矩阵LU，下一步就是基于矩阵L和向量b通过前代来计算哑向量y，采用前代解方程Ly=b得到y为

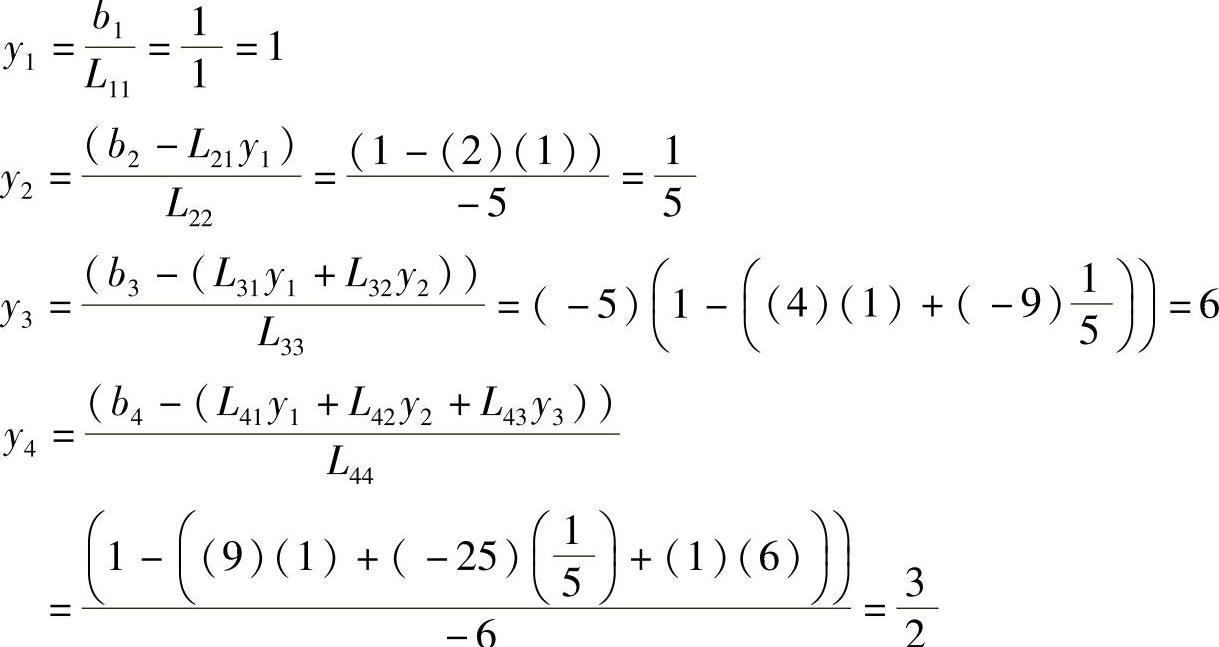
这样

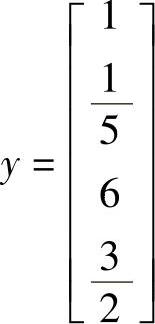
类似地，采用回代解方程Ux=y，可以得到解向量x为

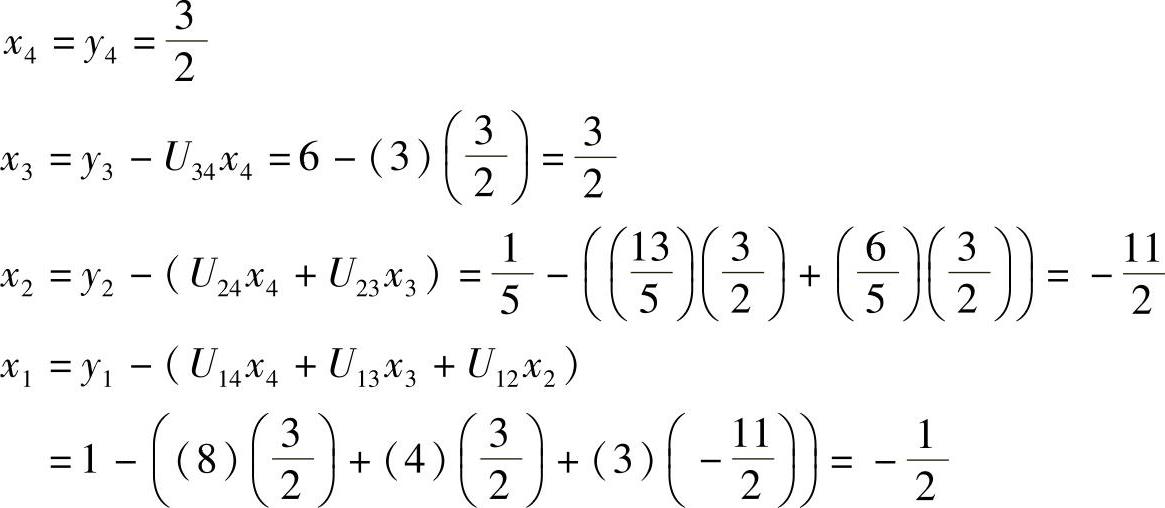
最终得到解向量

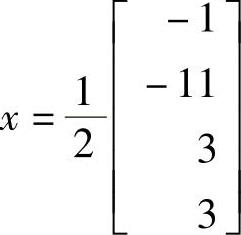
此解与例2.2中采用Gauss消去法和回代方法所得到的解是一样的。检查所得到的解是否正确的一种快速方法是将解向量x代回到线性方程组Ax=b中，看是否成立。