神经网络训练优化策略

前馈型神经网络在训练之前必须对权值和阈值进行初始化,在Matlab中应用newff()函数可以自动完成这一过程,然后应用init()函数使网络恢复到初始化的情况。神经网络的训练过程就是不断调整权值与阈值的过程,最终使神经网络的表现函数达到最小。本书在计算中将神经网络的表现函数设置为网络输出y和期望输出向量的误差平方和性能函数sse。

BP神经网络训练函数有traingd、traingdm、traingdx、trainrp、traincgf、trainlm、taaincgp、traincgb、trainscg、trainbfg、trainoss、trainbr等,每种训练函数各有特点,但是没有一种函数能适应所有情况下的训练过程。神经网络训练算法的选择非常重要,因为这关系到计算精度和收敛速度。以上提及的训练函数分别对应不同的训练算法,基本BP算法是沿着负梯度方向调整权值,但在实际应用中,BP算法很难胜任,为加快收敛速度出现了很多改进的BP算法。基于数值最优化理论的训练算法主要有共轭梯度法、高斯—牛顿法以及Levenberg-Marquardt方法(对应于trainlm函数)。图3-5所示的网络属于中小型网络,计算机的内存空间足够大,而且表现函数是平方和的形式,因此采用Levenberg-Marquardt方法来训练网络,Hessian阵可

以用下面的矩阵来近似替换:

其梯度为:

其中,J是Jacobian矩阵,它含有网络训练误差的一阶导数,是权值和阈值的函数,e是网络训练误差矢量。

则

当μ＝0时,算法为近似Hessian阵的牛顿法,当μ较大时,算法接近小步长的梯度法。在迭代过程中,如果训练成功,就减小μ的值；如果训练失败,就增加μ的值,表现函数最终会减小到一定值。以硝酸钾/木炭/硫黄体系的网络训练为例,为了确保仿真结果与试验结果的一致性,网络输入为有噪声信号,即10个水平下三组分的不同配比(3×10)的元素组成(6×10),期望函数(试验数据)为体系气相产物(CO、CO2、H2O、H2S、N2、SO2)组成、定压爆温、火药力(8×10)的试验测试值(见表3-1)。

表3-1　硝酸钾/木炭/硫黄体系烟火药训练样本矩阵

参数初始化:(www.xing528.com)

最大训练次数:net.trainParam.epochs＝300；

训练要求精度:net.trainParam.goal＝0；

最大失败次数:net.trainParam.max＿fail＝5；

最小梯度要求:net.trainParam.min＿grad＝1e-5；

最大训练时间:net.trainParam.time＝inf；

显示迭代过程:net.trainParam.show＝5。

其训练过程如图3-5所示。

图3-5　LM法训练网络的过程

从图3-5的训练过程可以看出,当计算量为100次时,仿真结果与实验值的相对误差接近10-4,据此认为算法的精度满足使用要求。

利用BP人工神经网络预测黑火药燃烧热力学参数的程序框图如图3-6所示。

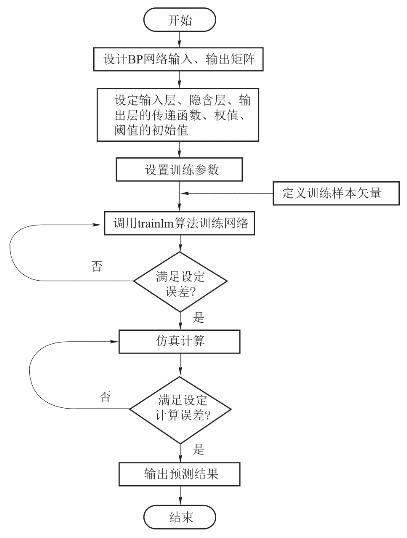
图3-6　基于BP网络的黑火药热力学参数计算程序框图