基于改进BP算法的前馈型神经网络模型建立

基于改进BP算法的前馈型神经网络通常有输入层、输出节点以及处于二者之间的一个或多个隐含层组成。如图3-1所示为神经元网络结构示意图。对于输入信息要先向前传播到隐含层的节点上,经过各单元特性的传递函数(也称为作用函数、激活函数、转换函数或映射函数等)运算后,将隐含节点的输出信息传播到输出节点,最后给出输出结果。网络的学习过程由正向和反向传播两部分组成。在正向传播过程中,每一层神经元的状态只影响到下一层神经元网络。若输出层得不到期望输出,即实际输出值与期望输出值之间有误差,就会转入反向传播过程,将误差信号沿原来的连接通路返回,通过修改各层神经元的权值,逐次向输入层传播去进行计算,再经过正向传播过程,这两个过程的交替运算,使得误差信号最小。当误差达到设定要求时,网络的学习过程结束。

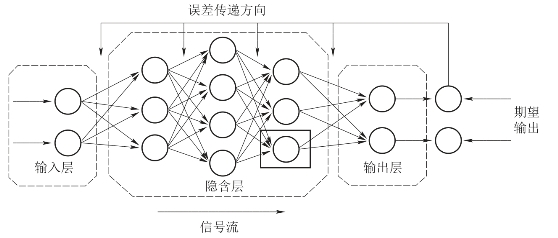
图3-1　基于BP算法的神经元网络结构图

图3-1中黑色方框表示的单个神经元输入、输出特性的细节如图3-2所示。

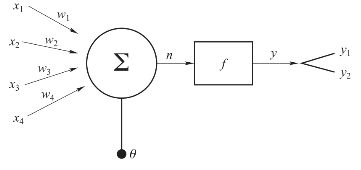
图3-2　神经元的数学模型

图3-2中x1、x2、x3、x4是神经元的输入,即来自前级四个神经元的轴突信息；θ是神经元的阈值；w1、w2、w3、w4分别是神经元对x1、x2、x3、x4的权值连接,即突触的传递效率；y是神经元的输出；f是传递函数,其决定了神经元受到输入x1、x2、x3、x4的共同作用达到阈值时以何种方式输出。

从以上结构示意图分析可知,构建前馈型BP神经网络需要确定三方面的内容:

(1)确定合理的信息表达方式,将已知数据样本处理成输入-输出模式的矩阵。(www.xing528.com)

(2)选择网络参数,确定输入、输出神经元的数目,隐含层层数以及每层神经元的数目。

(3)选择网络模型,确定传递函数、连接方式、各神经元的相互作用等。

引入人工神经网络技术的目的在于抛开燃烧理论模型,仅通过已知样本的训练仿真得到烟火药配方组成与这些参量的函数关系。研究关注的重点是黑火药体系的气相产物种类、含量以及爆温、火药力等特性参数,首先将部分实验数据摘录出来,作为网络学习样本,依据拟解决问题的特点,我们选择BP神经网络,BP网络的构架由一个输入层、一个隐含层及一个输出层组成。其中输入层为6×10的矩阵,表示10个配方中元素丰度(C、H、O、N、S、K),相应地给出期望输出矩阵；隐含层神经元的数目对网络有一定影响,神经元数目太少会造成网络的不适性,但是神经元数目太多又会引起网络的过适性,根据经验选定隐含层的神经元个数为20；输出层的神经元个数为8,分别代表体系的火药力、爆温以及气相产物CO、CO2、H2O、H2S、N2和SO2的含量。BP中隐含层神经元的传递函数通常采用sigmoid型函数,根据问题需要,将隐含层神经元传递函数选定为tan-sigmoid型函数tansig(),输出层神经元传递函数为纯线性函数purelin()。这是因为如果选择输出层为sigmoid型神经元,则整个网络限制在一个较小的范围内；选择purelin型神经元,则整个网络的输出可以取任意值。如图3-3所示为sigmoid型和purelin型神经元传递函数形式。

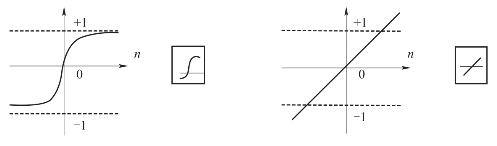
图3-3　神经元传递函数

(a)tan-sigmoid型传递函数；(b)purelin型传递函数

据此可以得到用于仿真烟火药燃烧反应特征输出的BP网络结构,如图3-4所示。

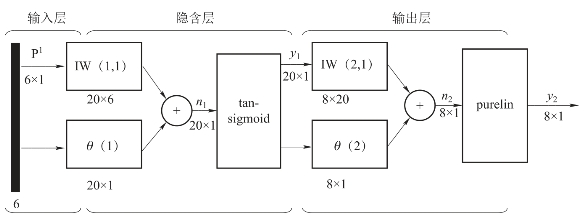
图3-4　用于仿真计算的两层BP网络结构