电力系统自动装置的基本原理

随着电力系统规模的日益增大，系统中所发生的故障，特别是一些系统性的重大故障将对电力系统的运行稳定性造成重大损害，进而导致电力用户因停电蒙受重大损失。虽然电力系统继电保护装置能够对电力系统中所发生的部分故障采取一定的保护措施，但是继电保护装置的保护仅是针对电力设备元件的，对于系统性的重大故障的保护并不十分完备，因此，电力系统自动装置作为电力系统继电保护与安全装置的补充与完善是十分必要的。

电力系统自动装置是为了保证电网安全稳定运行，保证电能质量，提高电网经济效益，实现电网运行操作的自动控制装置。目前，电力系统自动装置的种类繁多，主要包括发电机自动解并列同期装置、发电机自动励磁装置、电力系统频率及有功功率自动调节装置、电力系统自动低频减载装置、电力系统自动低压减载装置等。本书仅对实验教程所涉及的电力系统自动低频减载及自动低压减载的基本原理进行简单说明。

2.5.3.1 电力系统自动低频减载

1）电力系统的频率特性

根据电力系统的基本原理可知，电力系统频率反映了发电机组发出的有功功率与负荷所需有功功率之间的平衡状况。当电力系统中的电源（发电机组）发出的有功功率难以满足用户需求时，也就是发电机发出的有功功率总和与用户负荷有功功率总和出现差额时，系统频率就会偏离额定频率，当电源发出的有功功率小于用户负荷有功功率时，系统频率下降，反之，系统频率上升。

由电力系统稳态分析理论可知，在稳态条件下，电力系统频率是一个全系统一致的运行参数。电力系统频率f与发电机组转速n有如下关系：

式中：f——系统频率；

p——发电机极对数；

n——发电机组每分钟转数。

假设系统中有m台发电机组，n个负荷，发电机组原动机的功率为PSi（i=1，…，m），所发出的电功率为PGi（i=1，…，m），负荷功率为PLk（k=1，…，n），在稳态情况下，忽略机组内部损耗，则有：

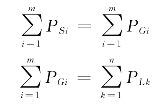
此时，系统处于功率平衡状态。

如果由于系统出现故障或其他状况，系统中的负荷突然变动，使得发电机组功率增加ΔPL，此时，机组功率小于负荷要求的电功率，要保持系统功率的平衡，机组只有把转子的部分动能转换为电功率，致使机组转速下降，其关系如下：

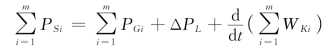
式中：WKi——发电机组动能。

可见系统频率的变化是由于原动机输入功率与发电机负荷功率之间失去平衡所致。负荷有功功率的变化将导致电力系统频率的变化。

当电力系统频率变化时，整个系统的有功负荷也将改变，即有：

式中：PL——系统的有功负荷。

上式表明，电力系统有功负荷随频率的变化而改变，这种特性称之为电力系统负荷的功率频率特性，即负荷的静态频率特性。

电力系统负荷的功率频率特性一般可表示为：

式中：PL——系统运行频率为f时，整个系统的有功负荷；

fN——系统额定频率；

PLN——系统频率为额定值fN时，整个系统的有功负荷；

a0，a1，…，an——为各类负荷占PLN的比例系数。

上式称之为电力系统有功负荷的静态频率特性方程。由此方程可以看出，当发电机组的输入功率与负荷功率失去平衡时，系统负荷参与了系统频率的调节作用，称之为负荷的调节效应。负荷调节效应的大小可以用下式衡量：

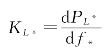
式中：KL*——负荷频率调节效应系数（标幺值）；

f*——系统频率的标幺值；

PL*——系统频率为f*时，整个系统的有功负荷标幺值。

正常运行时，频率变化较小，系统有功负荷与频率的关系可以看成一条直线，因此，负荷频率调节效应系数可表示为：

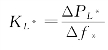
式中：ΔPL*——单位时间内负荷有功功率变化量的标幺值；

Δf*——单位时间内频率变化量的标幺值。

用有名值表示为：

通过上述分析可知，电力系统的有功负荷与频率的关系特性可以用负荷的功率频率方程表征，是电力系统负荷的静态频率特性，负荷频率调节效应的大小由负荷频率调节效应系数决定。

根据电力系统自动装置原理可知，对于一个有许多发电机及负荷的电力系统来说，系统中的发电机都是同步运行的，当系统中出现功率缺额时，忽略各节点之间的频率差，可以将系统中的所有发电机组等值为一台发电机组；同样，系统中的所有负荷也可等值为一个负荷。基于系统等值的方法，电力系统频率变化时，等值机组的运动方程可表示为：

式中：PG*，PL*——以系统发电机组总额定功率为基准的发电机组总功率与总负荷的标幺值；

Tx——等值机组惯性时间常数；

ω*——等值机组的旋转角速度。

假设：

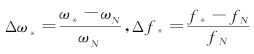
式中：ωN，fN——分别为系统等值机组的额定角速度和额定频率，其他符号含义同上。

则有：

将式（2.62）代入式（2.61）得：

式（2.63）就是电力系统频率动态特性，其右端就是系统的功率缺额，表明系统的功率缺额与系统频率的变化率（dΔf*/dt）是直接相关的。

2）电力系统自动低频减载原理

在电力系统中，当发生系统短路故障时，特别是发生较大事故时，系统将出现严重的功率缺额，此时，即使令系统中运行的发电机组发出其可能提供的最大功率，仍难于满足负荷功率需求，所引起的系统频率下降值将超出系统安全运行所允许的范围。在这种情况下，从保障系统安全性的角度出发，为保证重要用户的供电，必须采取应急措施，切除部分负荷，使系统频率恢复到安全范围内。

电力系统自动低频减载（Automatic Under Frequency Load Shedding，AUFLS）装置是为防止发生上述事故的重要装置之一，当系统频率下降时，采取迅速切除不重要负荷的办法来抑制频率的下降，从而保障系统安全性，阻止事故的扩大。

根据电力系统负荷的功率-频率特性可知，当系统频率降低时，负荷将按照其自身的功率频率特性，减少了从系统中所取用的功率，使之与发电机组所发出的功率保持平衡，也就是系统负荷所减少的功率等于功率缺额。

假设，用ΔPh表示功率缺额值，则由式（2.60）可得：

在实践应用中，KL大多使用标幺值KL*表示，则式（2.64）可表示为：

式中符号含义同式（2.59）。

对于我国电力系统来说，系统频率fN=50 Hz，则上式可写为：

式中：ΔPh%——功率缺额的百分数。

当系统发生严重的功率缺额时，电力系统自动低频减载装置的主要任务就是迅速断开相应数量的有功负荷，使系统频率在不低于某个允许值的情况下，达到有功功率的平衡，确保电力系统的安全稳定运行，防止事故的扩大。

自动低频减载装置从根本上来说是按照系统最大功率缺额数值进行负荷切除的。一般情况下，当系统发生事故时，为了保证系统稳定性，通常并不要求系统频率恢复至额定值，恢复频率低于额定值，大约在49.5～50 Hz之间。

假设，自动低频减载装置可能切除的最大负荷功率为ΔPL.max，而系统最大功率缺额为ΔPh.max，则根据式（2.64）可得：

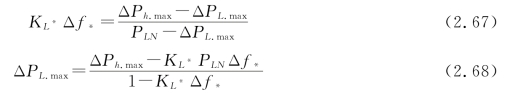(www.xing528.com)

式中：Δf*——系统额定频率与恢复频率fh差值的标幺值，其他符号含义同上。

在式（2.68）中，要确定可能切除的最大负荷功率ΔPL.max，必须先确定系统最大功率缺额ΔPh.max，进而进行负荷切除。

由式（2.63）所示的电力系统动态频率特性可以看出，频率下降速度d f*/dt隐含了功率缺额信息，因此自动低频减载装置在设定动作频率的基础上，考虑频率下降速度d f*/dt进行分级动作，可以根据频率变化率的大小来决定切除的负荷量。频率变化率越高，切除的负荷量就越多；反之，频率变化率越小，切除的负荷量越小。

总之，上述基本原理是自动低频减载装置功能实现的基础。在实践应用中，各个厂商的自动低频减载装置在动作原理及参数整定方面会略有不同，具体请参阅装置的说明书。

2.5.3.2 电力系统自动低压减载

1）电力系统的电压稳定及其特性

电力系统的稳定运行是保证为用户连续、可靠供电的前提。根据电力系统暂态分析理论可知，电力系统的稳定问题包括功角稳定和电压稳定。电力系统功角稳定问题经过人们的长期研究与实践，相关技术相对较为成熟，在此不再赘述。对于电力系统的电压稳定问题，国内外学者也进行了大量的研究工作，取得了许多重要成果。但是，近年来国内外发生的一系列重大电网安全事故表明，电压崩溃是导致电力系统失去稳定，并进而造成电网大面积停电事故的重要原因。

根据电力系统暂态分析理论，电力系统电压稳定的主要要求是保证系统的无功平衡，也就是系统中所有电源发出的无功功率在任何时候都要等于负荷所消耗的无功功率和系统损耗的无功功率之和。当系统中无功负荷大于无功出力时，系统电压就会下降；反之，系统电压就会上升。

在电力系统中，系统的无功电源主要包括发电机、同步调相机、静止电容器、静止补偿器等；无功功率损耗主要包括各级变压器及输电线路在传送电能时所消耗的无功。

对于同步发电机来说，发电机发出的有功功率与无功功率可分别表示如下：

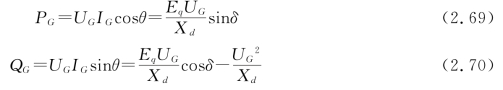
式中：Eq——同步发电机电势，即空载电压；

UG——发电机定子端输出电压；

IG——发电机定子端输出电流；

δ——发电机功角；

θ——发电机定子输出电压与电流之间的夹角。

式（2.70）就是发电机的无功-电压特性。从式（2.70）可以看出，发电机输出电压的平方与发电机输出的无功功率直接相关，其无功-电压特性曲线如图2.32所示。

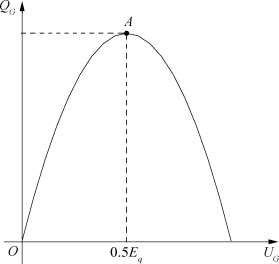
图2.32　同步发电机无功-电压特性曲线图

对于电力系统负荷来说，主要包括异步电动机负荷及恒定阻抗负荷。

异步电动机的无功功率由激磁电抗吸收的无功功率及定、转子漏抗吸收的无功功率构成，可用式（2.71）及式（2.72）表示。

异步电动机激磁无功功率Qm为：

式中：Xm——励磁电抗；

U——异步电动机的机端电压。

异步电动机定子和转子漏抗损耗的无功功率Qs为：

式中：Xt——定子与转子电抗之和；

Is——异步电动机的机端电流。

对于恒定阻抗负荷，其无功功率为：

式中：Xz——恒定阻抗负荷之电抗；

Iz——恒定阻抗负荷的电流。

电力系统负荷的无功-电压特性可表示为：

由式（2.74）可得到电力系统负荷的无功-电压特性曲线如图2.33所示。

根据电力系统的电源无功-电压特性及负荷无功-电压特性，可以确定电力系统静态无功-电压特性曲线如图2.34所示。图中QG（U）为发电机无功-电压特性曲线，QL（U）为负荷无功-电压特性曲线，正常运行时，发电机无功功率与负荷无功功率相等，即稳定运行点为两条曲线的交点A，A点电压为额定电压UA，处于无功功率平衡状态；当发生事故时，系统的负荷无功功率增大，负荷无功-电压曲线变为，新的稳定运行点为C点或B点。此时，若电源无功调节能够迅速调整，则运行点过渡到C点，达到新的无功功率平衡；如果电源无功功率调节速度无法适应负荷无功功率需求，则运行点会从A点向B点过度，电压进入不稳定区域并迅速跌落，导致电压崩溃。此时，可以切除部分负荷，使无功-电压特性曲线从变回至QL（U），恢复至电压稳定运行点。

电力系统受到干扰后保持系统稳定的充分条件为：

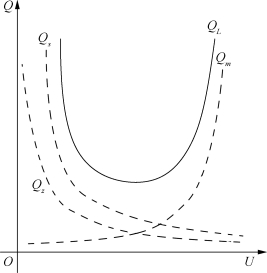
图2.33　负荷无功-电压特性曲线图

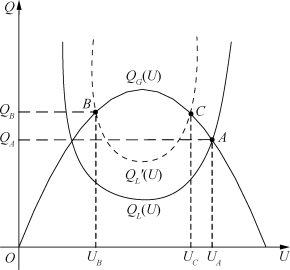
图2.34　电力系统无功-电压特性曲线图

自动低压减载指的是在电力系统发生严重故障、运行电压跌落至失稳边缘时，通过切除部分负荷使系统电压恢复，同时保留足够的功率裕度。自动低压减载被认为是经济而有效的防止电压崩溃的紧急控制措施。

综上所述，在电力系统发生事故或异常情况下，根据电力系统无功-电压特性，自动低压减载装置通过监测电压的变化，进而进行负荷切除，可以迅速调整系统的无功平衡状态，避免电压崩溃，实现系统的稳定运行。

2）电力系统自动低压减载原理

由上一节所述的电力系统无功-电压特性（Q-V曲线）可知，电力系统在故障情况下，自动低压减载装置可以根据电压跌落的状况，切除部分负荷，使系统达到新的无功平衡点，避免电压崩溃。但是，自动低压减载装置要能够有效动作，必须合理地确定切除负荷量及动作轮次。目前常用的方法是根据系统遭受扰动后能够避开电压临界稳定点的原则来确定最佳切除负荷量。然而，上述方法是基于静态负荷模型的，考虑的因素并不完备。

目前，根据国内外电网运行的实际经验，自动低压减载装置的配置整定通常采用Q-V曲线与P-V曲线（有功-电压曲线）相结合的方式来规划切负荷方案。

对于自动低压减载装置，有必要从电力系统的有功-电压特性（P-V曲线）的角度进一步理解低压减载的作用。

假设有一个简单电力网络如图2.35所示，发电机G经一段输电线路向负荷供电，其中，发电机电压为，负荷功率为P+j Q，负荷等效阻抗为，φ为负荷功率因数角，负荷节点电压为，电源与负荷之间的线路阻抗为，线路电流为。

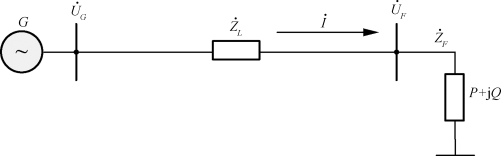
图2.35　简单电力网络接线图

由图2.35可得：

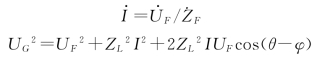
负荷节点电压为：

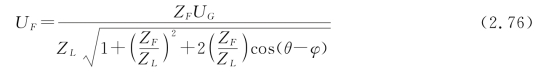
负荷的有功功率为：

由式（2.76）和式（2.77）可得负荷节点电压及其消耗的有功功率的关系P-V曲线，如图2.36所示。

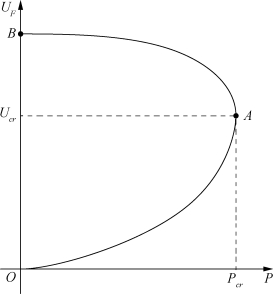
图2.36　P-V关系曲线图

图2.36中的A点为电压静态稳定临界点，其对应的负荷节点电压和有功功率分别为临界电压Ucr和临界功率Pcr：

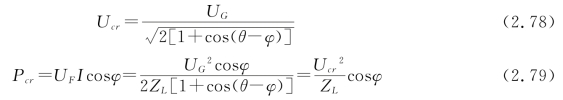
在P-V关系曲线图中，系统正常运行时，处于AB段，为稳定运行区域；当负荷扰动增加时，运行点向A点移动，当负荷增加到足够大时，运行点将越过A点，进入OA段，此时，电压跌落，处于不稳定运行状况，直至电压崩溃。因此，临界点A是电压稳定的关键点。

当系统运行点越靠近B点，也就是越远离临界点A时，系统越稳定，系统的稳定裕度也越大。因此，考察P-V曲线上的运行点远离临界点A的程度可以判定系统的稳定裕度。

根据上述理论，可以由P-V曲线确定系统运行点与临界点A之间的有功功率差额，作为自动低压减载装置切除的最大负荷量，再结合Q-V曲线验证所切除的负荷无功功率是否满足无功裕度要求，从而最终确定自动低压减载装置所要切除的负荷量及动作轮次。

由于系统电压跌落速率dU/dt隐含了功率缺额的信息，所以，在实践应用中，通常将电压下降的速率（dU/dt）和电压水平都作为低压减载的动作依据。

在工程实际中，通常将自动低压减载与自动低频减载功能置于同一台装置中，构成所谓频率电压紧急控制装置或自动低频低压减载装置，且不同厂商的装置原理及参数配置会略有不同，具体请查阅相关厂商装置的技术说明书。