剩余强度理论最早由美国帕特森空军基地非金属材料研究所的Whitney和Halpin等人在研究金属疲劳寿命预测方法过程中提出。他们假设树脂基复合材料的损伤累积过程可以用类似于金属材料中主裂纹扩展的机理来构建数学模型模拟。尽管他们没有建立一个类似于金属的标准裂纹扩展方程,但他们得到了剩余强度随载荷循环数变化的方程。由于主裂纹假设应用到复合材料寿命预测上存在很大的缺陷,许多学者又重新提出了自己的剩余强度理论。
一般而言,剩余强度理论在以下三个假设的基础上建立起来:
(1)材料的静强度服从一定的统计分布。如采用双参数Weibull分布拟合复合材料静强度分布试验数据,不仅可以得到满意的效果,同时在建立模型时也能简化理论推导的过程。此外也可以采用其他的统计分布类型,如三参数Weibull分布或对数正态分布等。
(2)在恒幅应力作用下,剩余强度与循环次数及最大外加循环应力之间的关系可以用一个确定性方程来表示。
(3)当剩余强度降低到最大循环应力(绝对值)水平时,就发生疲劳失效。
一个常用的剩余强度衰减模型为
![]()
式中 Sr——载荷Smax在n次循环作用后的剩余强度;
Sr-1——材料当前的剩余强度;
S0——材料的初始强度;
Smax——载荷谱中最大载荷;
n——载荷Smax作用循环次数;(https://www.xing528.com)
neq——载荷Smax作用后所达到与当前强度Sr等效的次数;
N——载荷Smax作用下材料失效的次数。
该模型表示,在恒幅疲劳载荷作用下,材料当前的强度与在静态测试下材料的初始强度无关,并且材料的失效是由于剩余强度不足以维持下一个施加在构件上的瞬间载荷导致的。在变幅载荷作用下,材料剩余强度需根据逐个循环载荷确定。由于大部分循环载荷具有不同的幅值Sa和均值Sm,因此等效载荷循环次数neq需根据当前材料强度和名义疲劳寿命N确定。
值得注意的是,在式(5-30)中,虽然当前载荷循环中的幅值Sa和均值Sm没有被表明,但是它们已经隐含在循环次数N中,该循环次数可由等寿命疲劳图求得。因此等寿命疲劳图不论是在Miner线性理论还是剩余强度理论中都发挥重要作用。
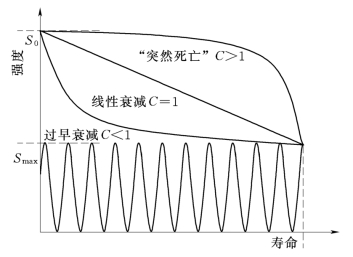
图5-11 不同的强度衰减模型图
式(5-30)中参数C表明了强度衰减特征:当C=1时,表示强度线性衰减;当C<1时,表示强度过早衰减;当C>1时,即出现“突然死亡”现象,不同的强度衰减模型如图5-11所示。
为了更准确地确定材料疲劳测试中参数C的值,需进行以下测试步骤:
(1)至少进行三种典型的试件疲劳测试,即拉—拉疲劳、压—压疲劳和拉—压疲劳测试。
(2)进行多种不同应力比r的材料拉、压剩余强度测试。
(3)进行多种应力水平的测试,即低应力—多次循环和高应力—少次循环测试。
(4)进行大量基本完全相同的材料试件测试,以满足方程中对数据的需求。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




