使用S-N曲线法优化工程耐久性

材料的S—N曲线也称为伍勒（Wohler）曲线，它表示的是所施加的应力水平S和疲劳寿命N之间的关系曲线，可通过多种不同应力水平的疲劳试验而获得。通常情况下，用一组标准试件（通常7～10件）在给定应力比r下施加不同的应力幅进行疲劳试验，记录对应的寿命为N，即可得到S—N曲线，材料的S—N曲线如图5-2所示。

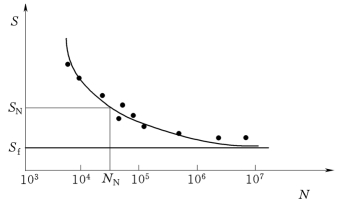
图5-2　材料的S—N曲线

由图可知，在给定应力比下，应力S越小，寿命N越长，当应力S小于某一极限时试件不会发生破坏，寿命N趋于无限长。

在S—N曲线中，对应于寿命应力NN称为N循环的疲劳强度SN。当寿命N趋于无限长Nf时，对应的应力极限值Sf称为材料的疲劳极限。

由图5-2可知，试验数据点并非完全吻合光滑曲线，这与试验条件和材料自身属性有关。根据试验数据点分布，通常情况下疲劳寿命N的指数形式与应力水平S或应力水平S的指数形式呈线性关系。下面介绍几种比较经典的S—N曲线表达式函数。

5.2.1.1　幂函数形式

幂函数形式的S—N曲线表达式为

式中 m，C——与材料性能、试件形式及加载方式等有关的参数，可由试验确定。

对式（5-1）两边取对数，则有

令a=lg C，b=-m可得

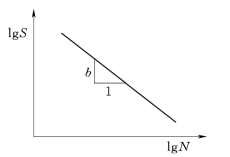
图5-3　幂函数形式下的S—N曲线

幂函数形式下的S—N曲线如图5-3所示，幂函数表达式表明在双对数坐标中lg S和lg N呈线性关系。

5.2.1.2　指数函数形式

指数函数形式的S—N曲线表达为

式中 m，C——相关参数。

对式（5-4）两边取对数，可得

令a=lgC，b=-mlge可得

指数函数形式下的S—N曲线如图5-4所示，指数函数表达式表明在单对数坐标中S与lg N呈线性关系。(www.xing528.com)

5.2.1.3　三参数函数形式

在预先知道材料的疲劳极限Sf的情况下，S—N曲线可表示为

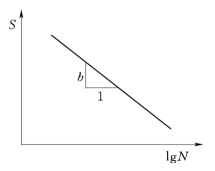
图5-4　指数函数形式下的S—N曲线

式中 m，C——相关参数；

Sf——疲劳极限参数。

当应力S趋近于疲劳极限应力Sf时，寿命N趋于无穷大。

5.2.1.4　其他S—N曲线表达式

1977年美国学者D.F.SIMS提出了改进的指数表达式，表达式中的参数具有应力比r相关性，且参数由最小二乘法求得，即

式中 a，b，c，x，y——拟合参数。

1988年，意大利学者G.Caprino提出了双参数，并考虑了强度下降的S-N曲线表达式为

式中 S0——材料的初始强度；

a，c——拟合参数。

随后，澳大利亚学者Epaarachchi，J.A和Clausen，P.D将式（5-10）扩展为三参数形式，并将应力比r对纤维方向和实验频率因素考虑其中，即

式中 ψ——应力比相关参数；

θ——主方向纤维角；

f——实验频率。

多数情况下，S—N曲线被用来描述在横幅循环载荷作用下试件寿命，为了描述不同成活率P下的S—N曲线集，在疲劳寿命研究中引入了P—S—N曲线。该曲线给出了：

（1）在给定应力水平下失效循环次数N的分布数据。

（2）在给定有限寿命下的疲劳强度S的分布数据。

（3）无限寿命或N＞Nf的疲劳强度—疲劳极限的分布数据。