Darrieus型风力机的重要结构参数包括扫略面积、叶片展弦比、叶片数、翼型、实度以及叶片形状。
4.1.2.1 扫略面积
风轮旋转扫过的面积在垂直于风向的投影面积是风力机截留风能的面积,称为风力机的扫掠面积,其大小直接决定总的捕获能量。扫略面积由风力机风轮半径、高度等尺寸决定。设计过程中,由设计额定功率、额定转速、风能利用系数可估算出扫略面积,进而确定风力机各部件尺寸范围。很多学者和科研单位进行了垂直轴风力机尺寸优化,试图找出风力机性能和成本综合最优方案,但得到的结论均不统一。
4.1.2.2 叶片展弦比
叶片展弦比是叶片高度与叶片弦长的比值。当叶片以一定的速度运行时,叶片压力面空气压强较高,而叶片吸力面空气压强较低,叶片产生向上的升力。由于叶片表面存在压差,压力面处气体会由叶片两端向上方绕动,产生翼尖涡。翼尖涡会扰乱叶片两端气流的正常流动,减小叶片的升力,叶片的升力系数越大则涡的影响越大,并且翼尖涡会在叶端后方形成一串的涡流,产生涡诱导阻力,造成叶片阻力增加。如果叶片展弦比较大,翼尖涡造成的升力损失与阻力增加与叶片的升力与阻力相比可忽略不计;如果叶片展弦比较小,翼尖涡造成的升力与阻力损失比较明显。但是,当叶片长度有限时,展弦比越大,叶片弦长就越小,叶片面积也就越小,从而导致总升力减少。此外,叶片弦长减少会导致叶片雷诺数减小,进而使叶片失速攻角减小、最大升力系数减小、阻力系数增加。因此,既要尽量保证叶片弦长足够大,又要避免展弦比小造成的弊端,某些风力机借鉴航空技术,在叶片顶端加装端板,可大大减小绕流的影响。
4.1.2.3 叶片数
叶片数量直接决定风力机成本、气动性能和结构载荷分布。目前,Darrieus型风力机叶片数多为三叶片和双叶片。三叶片风力机制造技术较成熟、气动性能好、扭矩波动小,因此三叶片风力机应用最多,但是双叶片风力机材料和安装成本比三叶片低得多,因此双叶片风力机也具有一定应用空间。此外,许多学者开展了四叶片甚至更多叶片型式风力机研究。三叶片风力机和双叶片风力机性能对比见表4-1。
表4-1 三叶片和双叶片Darrieus型风力机性能对比

4.1.2.4 翼型

图4-4 NACA0015翼型
翼型直接决定了风力机风能转换效率、叶片成本、风力机载荷,升阻比是反映翼型性能的一个重要指标,其值越高,代表翼型气动性能越好。NACA00XX系列对称翼型具有高升力、低阻力、失速特性良好等优点,因此大多数Darrieus型风力机采用该系列翼型,其中使用最为广泛的是图4-4所示的NACA0015翼型,该翼型在180°攻角范围内具有对称的升力和阻力特性,俯仰力矩系数为零,且在风轮旋转过程中不会产生反向力矩。
4.1.2.5 实度
实度指叶片展开曲面面积除以扫略面积,是Darrieus型风力机关键结构参数之一,其取值应综合考虑其他主要参数,其计算公式为

式中 ξ——实度;
B——叶片数;
c——叶片弦长;
l——叶片长度;
A——扫略面积。
简便起见,通常认为垂直轴风力机的实度为
![]()
式中 R——风轮半径。
如图4-5所示为不同实度的风轮在不同叶尖速比时的风能利用系数曲线图,显示了实度从0.1~0.4时的功率系数随尖速比的变化。实度大的适应风速变化范围窄,实度小的适应风速变化范围大。
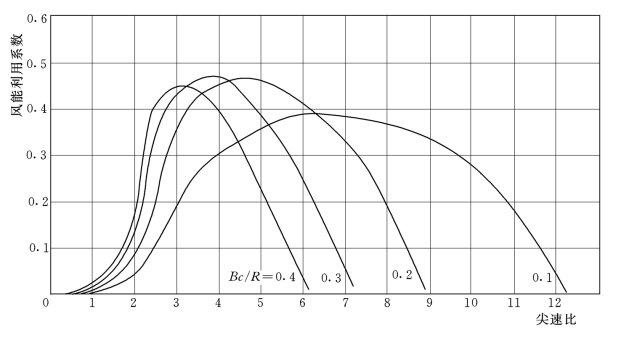
图4-5 不同实度对风能利用系数的影响
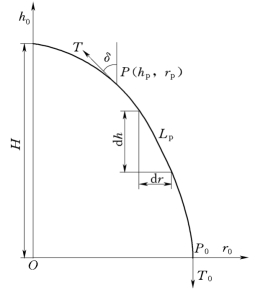
图4-6 Troposkien曲线
4.1.2.6 叶片形状
经过多年的研究和实践,Darrieus型风力机叶片形状逐渐发展成以下几种曲线:Troposkien曲线、Sandia曲线、悬链曲线和抛物线。其中,Troposkien曲线又分为忽略重力的理想Troposkien曲线和考虑重力的修正Troposkien曲线。
1.Troposkien线型叶片
将Troposkien曲线用数学公式表达出来是叶片形状设计中的重要环节,不同参数设定对叶片形状影响明显。图4-6中总长为L0,单位长度质量为m0的柔性叶片两端固定,绕固定轴旋转,受离心力作用自然弯曲成Troposkien曲线,取PP0段为研究对象,将PP0段的载荷进行正交分解,即
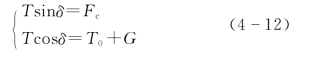
式中 δ——叶片张力T与垂直方向的夹角,取值范围为δ∈[0,π/2];
T——叶片张力;
Fc——离心力;
T0——材料极限承载力;
G——PP0段总质量。
式(4-12)中Fc和G分别表示为

式中 m0——Darrrieus型风力机叶片材料单位长度质量;
ω——叶片旋转角速度;
Lp——沿积分路径的曲线长度;
g——重力加速度。
由式(4-12)可以得到

由图4-6所示的几何关系可得到
![]()
综合式(4-12)~式(4-16),可以得到
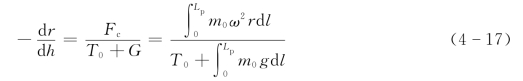
为求解式(4-17)中微分 -积分方程,需设定边界条件,即
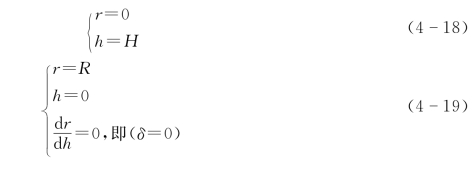
式中 H——风轮1/2高度;
R——赤道半径。
当角速度ω较大时,绳索的自重相对于张力、离心力量级较小,可忽略,从而得到
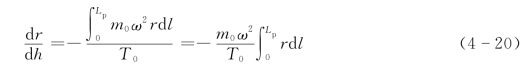
由图4-6所示的几何关系,可得到
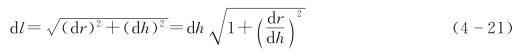
利用H对r和h无因次化,即可得

将式(4-22)代入式(4-20)可得
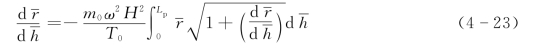
式(4-23)两边同时对dh求导,可得

其中

式(4-24)右侧根号项对dh求导,可得到
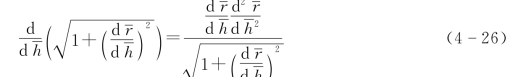
综合式(4-24)和式(4-26),可得到
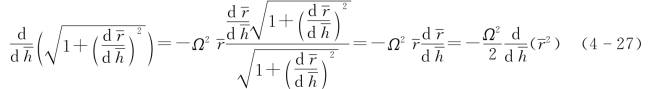
式(4-27)两边同时对dh积分,利用边界条件式(4-28)可得到式(4-29),即
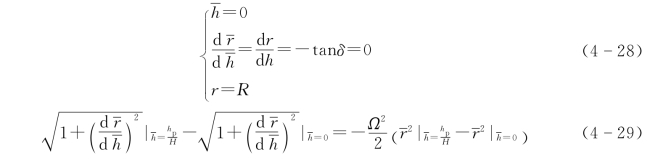
式中 hp——P点高度。
对式(4-29)进行整理可得
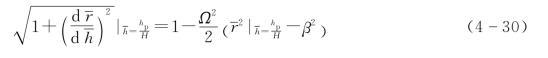
其中 ![]()
式中 β——径高比。
设定![]() ,式(4-30)左侧可写成式(4-31),联合式(4-30)和式(4-31)可得到式(4-32),即
,式(4-30)左侧可写成式(4-31),联合式(4-30)和式(4-31)可得到式(4-32),即
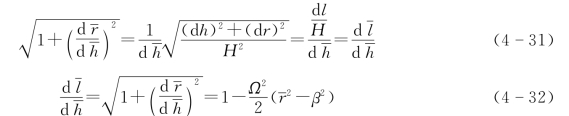
对式(4-32)两侧同时平方,可得到式(4-33),整理多项式后可得到式(4-34),即
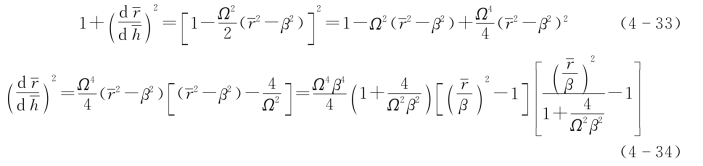
对式(4-34)等号两侧同时开根号,可得
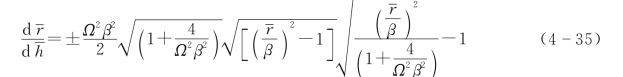
引入变量,代入式(4-35)可得
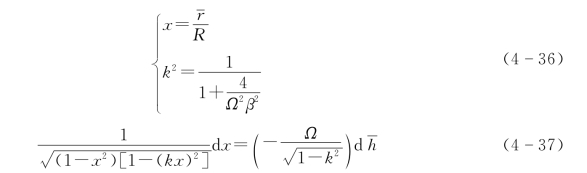
式(4-37)两侧同时积分,积分上下限取式(4-38)及式(4-39),可得到式(4-40),即
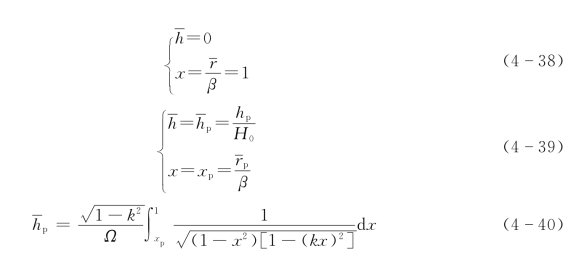
取值x=sinψ,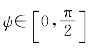 ,则d x=cos(ψ)dψ,替换式(4-40)中x,可得到式(4-41),即
,则d x=cos(ψ)dψ,替换式(4-40)中x,可得到式(4-41),即
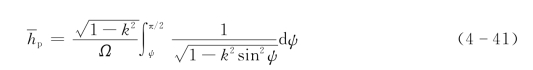
设定第一类椭圆积分,即
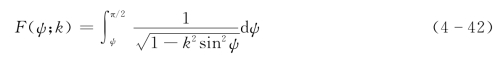
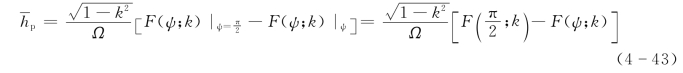
由于在Troposkien曲线的顶点存在边界条件,即
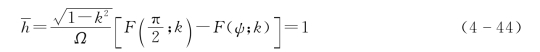
由于F(ψ;k)|ψ=0=0,因此可得
![]()
由于边界条件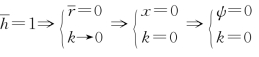 ,则可得Troposkien曲线的数学表达式为
,则可得Troposkien曲线的数学表达式为

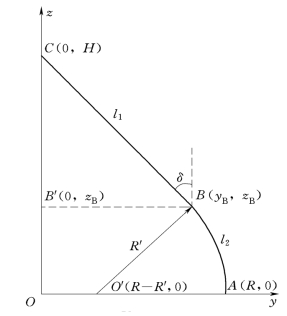
图4-7 Sandia型曲线
将式(4-46)代入已知条件并查询椭圆积分数值表,则可得到任意条件下的Troposkien曲线上点的坐标。(https://www.xing528.com)
2.Sandia线型叶片
实际应用中,Darrrieus系列风力机中Φ型风力机通常采用近似的Troposkien曲线叶片。Sandia型曲线从理想的Troposkien曲线简化而来。图4-7为Sandia型曲线,由下部圆弧段(AB)和上部直线段(BC)组成,整个叶片以中间的赤道面对称分布,l为叶片总长度,2H为风轮高度。
令B点的坐标为(yB,zB),则直线段![]() 的方程为
的方程为

其无因次形式为

其中,η=y/R,ζ=z/H,η∈[0,ηB],ζ∈[ζB,1];在B点,ηB=yB/R,ζB=zB/H。
在直线段CB上,其偏斜角δ1恒定,即

式中 β——径高比。
叶片总长度可表示为l=2(l1+l2),则
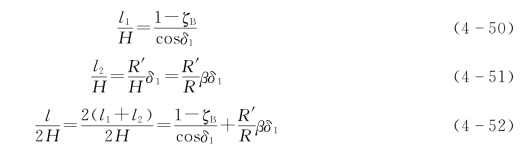
圆弧的圆心位置为O′(R-R′,0),且经过点A(R,0)和点B(yB,zB),则圆弧方程可表示为[y-(R-R′)]2+z 2=R′2,其无因次形式为
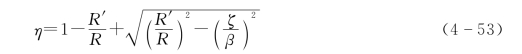
其中,η∈[0,ηB],ζ∈[0,ζB]。令δ2为圆弧的偏斜角,则

当ζ=ζB=zB/H,δ2=δ1时,可得

因此,式(4-53)可变换为

Sandia型风力机叶片总长度为l比总高2H得到

旋转叶片扫掠面积A可表示为
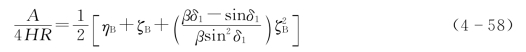
叶片最大旋转半径为

叶片的重心位于
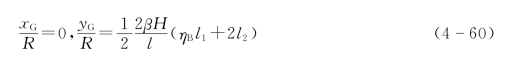
叶片的张力比可表示为
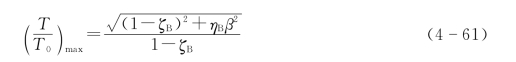
式中 T——叶片张力;
T0——材料极限承载力。
其中,叶片张力最大值Tmax发生在叶片与垂直轴相交处

最大张力系数(CTS)max为
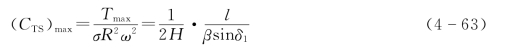
3.悬链线型叶片
假设一材质均匀、截面相同的完全柔性绳索,将其两端悬挂于A点和B点,在只有重力作用形成的线型称为悬链线,悬链线曲线如图4-8所示。
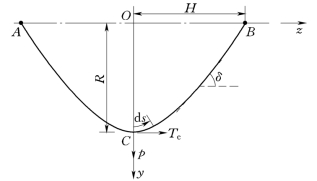
图4-8 悬链线曲线
悬链线型叶片截面受力平衡微分方程可表示为

其中 ![]()
式中 T——叶片张力;
d s——叶片某微元段弧长;
p——叶片单位长度上的荷载。
将式(4-64)分别沿y方向和z方向投影,可得

消去式(4-65)中的张力T可得

式中 K——常数。
式(4-66)还可以写成

令a=p/K,d y/d z=sinh u,对式(4-67)积分可得
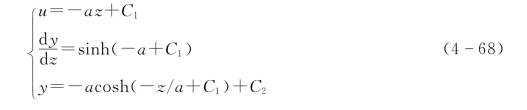
引入边界条件

确定积分常数C1、C2,即

由此,可得悬链线方程为
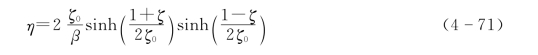
式中 β——径高比。
式(4-71)中,ζ=z/H,ζ0=a/H,η=y/R。
对于C点,η=1,ζ=0,将其代入式(4-71)可确定径高比β与常数ζ0的关系为
![]()
对于给定的径高比β值,可由式(4-72)计算出ζ0值。悬链线曲率半径γ为
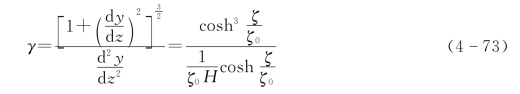
悬链线型叶片长度l表达式为

其无因次形式为

具有垂直对称轴的悬链线形状转子扫略面积A为
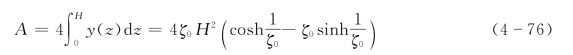
其无因次形式为

对于密度均匀的叶片,其悬链线重心在Oy轴上,距原点O的距离yG为
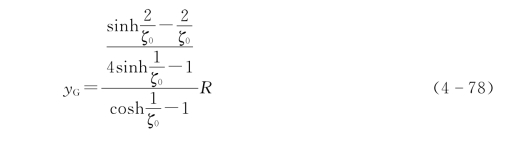
式中 R——赤道半径。
悬链线切线与水平方向夹角δ为

4.抛物线型叶片
抛物线形状可由悬链线得到,如图4-8所示,设张力Tc≫p,则b=Tc/p的值非常大。对cosh![]() 按泰勒级数展开
按泰勒级数展开
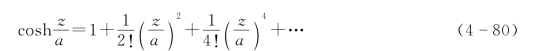
保留前两项,结合式(4-71)可得叶片抛物线方程为
![]()
式中 R——赤道半径。
式(4-81)的无因次形式为
![]()
其中,ζ=z/H,η=y/R,式(4-82)即为抛物线方程。赤道处的曲率半径为

式中 β——径高比。
抛物线型叶片长度l的无因次形式为
![]()
抛物线型叶片风轮扫略面积A为
![]()
式中 H——风轮1/2高度。
对于密度均匀的叶片,其抛物线重心在Oy轴上,距原点O的距离yG为

其中
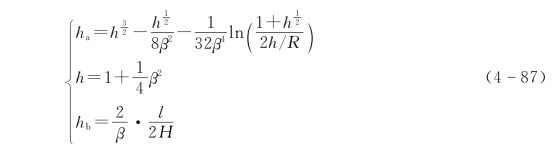
悬链线切线与水平方向夹角δ为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




