风力发电机的工作原理与特点

Savonius风力机的重要结构参数包括叶片重叠比和高径比。重叠比指两叶片之间的重叠宽度与叶片直径的比值，高径比指风轮高度与叶片直径的比值。Savonius风力机结构如图4-1所示，该风力机有两个半圆形叶片开口相对组成S形，并在旋转中心处有一部分重叠区，即在两叶片端部之间形成了一定的间隙，运行起来如同放大的杯形风速仪，气流可以从转轴处以及弯曲叶片交叠的间隙中间流过。当不考虑中心转轴直径影响时，叶片的重叠比OL和高径比AP为

式中 S——两叶片间重叠宽度；

d——叶片直径；

H——风轮高度。

如果风力机具有中心转轴，则需要除去转轴直径，其叶片的净重叠比OLn定义为

式中 a——转轴直径。

旋转角速度ω=k表示瞬时旋转向量，由于Savonius风力机的对称性，因此ω=为常数。基于Chauvin等提出的叶片压力下降数学模型，当OL=0时，双风轮的Savonius风力机的扭矩Q可以表示为

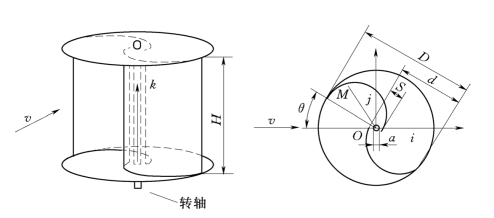
图4-1　Savonius风力机结构图

式中 OM——由转轴中心指向叶片上某点M的向量；

FM——过叶片上某点M沿叶片切线方向的力。

以上扭矩表达式可分为两个部分，见式（4-5）。第一部分与前行叶片相关，是风力机转子驱动部分，以QM表示；第二部分与后行叶片相关，是风力机转子阻力部分，以QD表示，即

假设作用在前行叶片和后行叶片上的气压差分别为ΔpM和ΔpD，则总扭矩可表示为

式中 r——重叠比OL为0时，Savonius风力机叶片的旋转半径；(www.xing528.com)

θ——风轮方位角。

平均功率P可以通过扭矩从0～π积分得到，即

风能利用系数由式（4-7）所示。根据风洞试验研究结果，两叶片的Savonius风力机风能利用率要高于三叶片。

式中 v——入流风速；

r——叶片半径。

美国Sandia国立实验室研究小组最早展开Savonius风力机叶片重叠比研究。在无转轴的条件下，对4种不同重叠比Savonius风力机进行风洞试验，结果表明，当OL=0.15时，风力机的气动性能最佳。

国内某试验小组对Savonius风力机进行了风速v=6m/s（雷诺数Re=2.5×105），3种重叠比（OL=0、0.2、0.5）下风力机输出功率系数CP与叶尖速比λ之间的关系的试验，Savonius风力机叶尖速比与功率系数关系如图4-2所示。

实际上，转轴在重叠区占据一定比例空间，必将对风力机的性能造成影响。日本牛山泉试验小组在有转轴情况下，对Savonius风力机进行了较为详细的风洞试验，得出最佳重叠比应设置在0.2～0.3范围内的结论。

Savonius风力机启动力矩系数Cts与风力机方位角之间的关系曲线如图4-3所示。启动力矩系数Cts的计算公式为

式中 Ts——启动力矩；

A——扫略面积；

D——风轮直径。

图4-2　Savonius风力机叶尖速比与功率系数关系

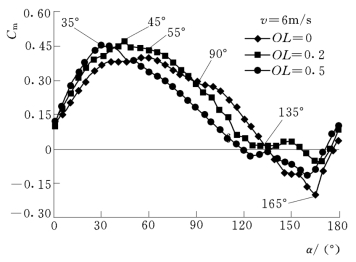
图4-3　风力机启动力矩系数与方位角关系曲线