数值离散方法的应用和优化

数值离散方法是指将控制方程进行离散化处理的方法，即用数值离散表达式代替控制方程中出现的偏导数，从而生成一个大型代数方程组，在给定定解条件的基础上，便可实现代数方程组的求解。CFD中所使用的数值离散方法主要有有限差分法、有限单元法、有限体积法以及面元法。

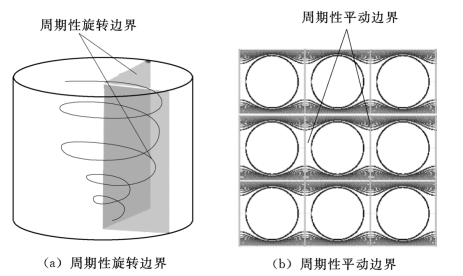
图2-20　周期性边界

2.6.4.1　有限差分法

有限差分法是CFD最早采用的数值离散方法，至今仍被广泛应用。有限差分法求解流动控制方程的基本过程是：首先将求解区域划分为差分网格，用有限个网格点代替连续的求解域，将待求解的流动变量（如密度、速度等）存储在各网格点上，并将偏微分方程中的微分项用相应的差商代替，从而将偏微分方程转化为代数形式的差分方程，得到含有离散点上的有限个未知变量的差分方程组。求解差分方程组，就得到了网格点上流动变量的数值解。

2.6.4.2　有限单元法(www.xing528.com)

有限单元法最早应用于结构力学，后来逐步应用到CFD。有限单元法的基本思想，是在力学模型上将一个连续的物体离散成为有限个具有一定大小的单元，这些单元仅在有限个节点上相连接，并在节点上引进等效力以代替实际作用于单元上的外力。对于每个单元，根据分块近似的思想，选择一种简单的函数来表示单元内位移的分布规律，并按弹性理论中的能量原理（或变分原理）建立单元节点力和节点位移之间的关系。最后，把所有单元的这种关系式集合起来，就得到一组以节点位移为未知量的代数方程组，解方程组就可以求出物体上有限个离散节点上的位移。

2.6.4.3　有限体积法

有限体积法又称为有限容积法，根据物理量守恒这一基本要求，以守恒型的方程为出发点，通过对流体运动的有限子区域的积分离散来构造离散方程。有限体积法有两种导出方式：①控制容积积分法；②控制容积平衡法。所导出的离散化方程，都描述了有限各控制容积物理量的守恒性，所以有限体积法是守恒定律的一种最自然的表现形式。该方法适用于任意类型的单元网格，便于应用模拟具有复杂边界形状区域的流体运动；只要单元边上相邻单元估计的通量是一致的，就能保证方法的守恒性；有限体积法各项近似都含有明确的物理意义；同时，它可以吸收有限元分割近似的思想以及有限差分方法的思想来发展高精度算法。由于物理概念清晰，容易编程，有限体积法成为了工程界最流行的数值计算手段。

2.6.4.4　面元法

面元法基本原理是将物体表面等特征面进行离散，生成网格后对每个网格用一个平面或曲面代替原来的物面，称为面元。在该面元上布置流动的奇点如源、涡、偶极子及其组合，从而进行求解气动问题。