任何流动都服从三大定律,即质量守恒定律、牛顿第二定律、能量守恒定律,在数学上通常以积分或微分形式的偏微分方程描述,也就是基本控制方程,包括连续性方程、动量方程以及能量方程,基本控制方程如图2-17所示。计算流体力学就是将这些方程中的积分或微分用代数的形式来表示,进而得到方程在时间、空间点上的离散解。
控制方程可分为守恒形式和非守恒形式,在气动理论分析中,采用守恒形式或者非守恒形式控制方程无关紧要,控制方程可从一种形式转化成另一种形式。但是,在计算流体力学中采用守恒形式还是非守恒形式控制方程关系重大,原因在于CFD将本来连续的流场用一系列的离散点来代替,因此必须采用一定的离散格式及数值计算方法,而正是这些离散格式及计算方法对于控制方程形式的不同适应性,导致了并非任何形式的控制方程均适用于CFD。
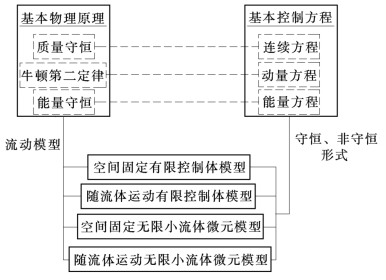
图2-17 基本控制方程
2.6.1.1 连续性方程
取流场中某任意形状的空间固定有限控制体,如图2-18所示,运用质量守恒定律,即单位时间内流进或流出表面S的流体质量等于控制体内质量改变速率。
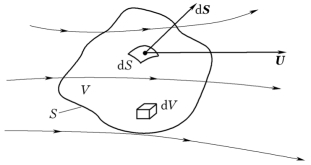
图2-18 空间固定的有限控制体
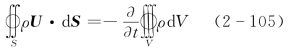
式中 ρ——流体密度;
U——流体速度向量;
S——控制体表面积,S=n S,n为表面单位法向向量;
V——控制体体积。
由于控制体是固定的,也就是积分限是固定的,所以式(2-105)可以进一步写成

采用高斯定理(又名散度定理)
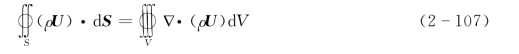
式中 ∇——哈密顿算子。
将式(2-107)代入式(2-106)得
![]()
由于该控制体是任意选取的,所以式(2-108)对任意的积分限都成立,由此可得

式(2-108)即为连续性方程的积分形式,式(2-109)为连续性方程的微分形式。
2.6.1.2 动量方程
取流场中某任意形状的空间固定有限控制体,如图2-18所示,运用牛顿第二定律,即
![]()
式中 F——控制体受到的合力;
m——控制体内流体质量;
a——加速度。
式(2-110)可进一步写成
![]()
控制体受到的合力包括体力与面力,体力有重力、电磁力等,面力有压力、黏性引起的剪切力等,合力、体力与面力的表达式为

式中 F1——体力;
f——单位质量流体受到的合体力。

式中 F2——面力;
p——流体压力;
Fviscous——黏性力。
式(2-111)右侧表示控制体流体动量对时间的改变速率,包括单位时间流进或流出控制体表面的净动量以及由于非定常流动引起的控制体在单位时间内的动量改变,即
![]()
根据式(2-111)~式(2-115)S,可得动量方程的V积 分形式,其表达式为
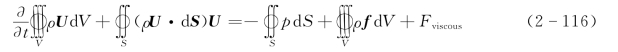
根据梯度理论,式(2-116)右侧的第一项可以表示为(https://www.xing528.com)

由于有限控制体是固定的,故积分限不变,式(2-116)可进一步写成
![]()
在笛卡尔直角坐标系中将U分解,即
![]()
式(2-118)在x方向的分量形式为
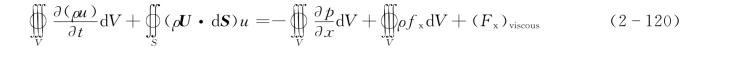
利用高斯定理,式(2-120)左侧的面积分可表示为
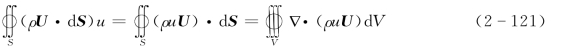
将式(2-121)代S入式(2-120)S中 ,可得
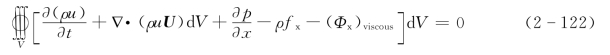
式中 (Φx)viscous——黏性力项。
由于有限控制体是任意选取的,故
![]()
式(2-123)为动量方程x分量的微分形式,同理可得y、z分量的微分形式为
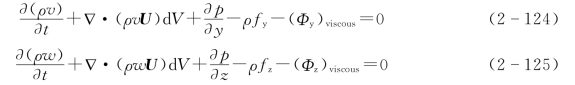
式(2-123)~式(2-125)又被称为纳维斯托克斯方程,即N S方程。
2.6.1.3 能量方程
对于不可压缩流体,密度ρ是常数,主要的流场变量为压力p和速度U,前面推导的连续性方程与动量方程就是关于未知量p和U的方程。因此,对于不可压缩流动问题,连续性方程和动量方程足够描述流场流动特性。但是,对于可压缩流动问题,密度ρ也是变量,两个方程不能求解三个未知量,必须再引入一个方程来完善基本控制方程体系,这个方程就是能量方程。
取流场中某任意形状的空间固定有限控制体,如图2-18所示,运用能量守恒定律,即控制体内流体与周围环境热量的传递速率加上外部对控制体内流体的做功速率,等于流体流经控制体的能量改变速率,即
![]()
式中 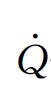 ——控制体内流体与周围环境热量的传递速率;
——控制体内流体与周围环境热量的传递速率;
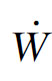 ——外部对控制体内流体的做功速率;
——外部对控制体内流体的做功速率;
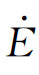 ——流体流经控制体的能量改变速率。
——流体流经控制体的能量改变速率。
式(2-126)各项具体表达式为
![]()
式中 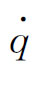 ——单位质量流体热量传输速率;
——单位质量流体热量传输速率;
![]() ——黏性作用引起的热量传输项。
——黏性作用引起的热量传输项。
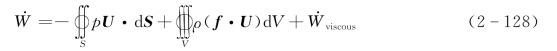
式中 ![]() ——黏性力做功速率项。
——黏性力做功速率项。

式中 e——单位流体质量的内能。
将式(2-127)~式(2-129)代入式(2-126)得

式(2-130)即为能量方程的积分形式,能量方程微分形式与连续性方程及动量方程微分形式的推导过程类似。由于控制体边界是固定的且是任意选取的,同时采用高斯定理可得

其中,等号左侧为控制体中能量的增加率,等号右边第一项为流进或流出控制体的净热量,第二项、第三项分别为面力和体力对控制体做功的速率,最后两项为黏性项。
以上推导了连续性方程、动量方程以及能量方程的积分形式和微分形式,三大基本控制方程含有4个流场变量,分别为ρ、p、U与e,方程组不封闭,因此必须再补充一个方程。本书主要讨论风力机流场计算,故流体可视为空气,假设气体为完全气体(理想气体),引入热力学状态方程,即
![]()
式中 cv——常数;
T——温度。
由于增加未知量温度T,故再引入式(2-133)
![]()
式中 R——气体常数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




