Leishman-Beddoes模型详解

1983年Beddoes提出了一个更复杂的可模拟附着流和分离流的动态失速模型，之后Leishman等人对其进行了修正，该模型相比于Gormont模型更加准确。

Leishman-Beddoes模型包括三个部分：非定常附着流、失速发生和分离流。非定常附着流的求解包括循环载荷和冲击载荷，这些载荷来源于随时间变化的附着涡。环量法向力系数的表达式为

式中 CNa——某一雷诺数下静态法向力系数的变化斜率；

n——迭代次数。

αEn是关于α的等式，即

式中 α——攻角；

Xn，Yn，Zn——亏损函数，根据经验且基于流体速度和俯仰角变化速率确定。

由式（2 88）、式（2 89）可以看出Leishman-Beddoes模型是一个迭代模型，在非定常附着流部分计算延时攻角的迭代公式为

其中　

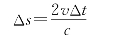
式中 Dαn——亏损函数；

Ta——依据经验的时间常数（对于NACA0015翼型，Ta=5.78）；

Δs——无量纲的时间步；

v——来流风速；

c——弦长。

由于气流在边界层处逆转，翼型表面将形成前缘涡，通过使用临界攻角αcr来表征动态失速的发生

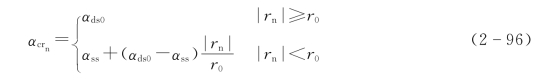
式中 rn——衰减俯仰角变化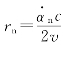速率，；

——俯仰角变化速率；

αss——静态失速攻角；

αds0——临界失速攻角。(www.xing528.com)

当n=0时，通过求得临界衰减俯仰角变化速率r0来界定准定常失速和动态失速的发生，动态失速的条件为

分离流的影响可以分为两个部分：尾缘处分离和前缘涡对流。尾缘处的分离和边界层分离点运动发生时间延迟有关，且通过Kirchhoff流可近似获得

式中 ——延迟分离点；

α1，S1，S2——基于翼型和当地雷诺数的常数。

围绕叶片本身的边界层具有时变性，并且这种影响还会在压力响应延迟上叠加，通过a′体现出来。这种附加的延迟通过动态分离点f″体现出来，即

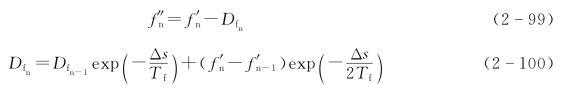
式中 Dfn——亏损函数；

Tf——经验时间常数。

动态失速发生前非定常条件中的法向力系数可表示为

当失速条件满足后，翼型表面的前缘涡对流向尾缘发展，在该过程中，法向力将会有一个较大幅度提升，即

式中 ——涡对流过程中的法向力系数（称为“涡升力”），依据俯仰角变化速率而定；

vx，B1——基于当地雷诺数和翼型的影响因子。

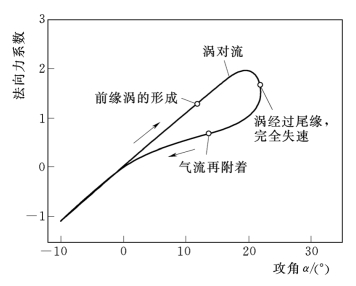
图2-16　Leishman-Beddoes模型计算的法向力系数随攻角变化示意图

当涡通过尾缘后，法向力会急剧下降，则总的法向力系数可表示为

切向力系数可通过Kirchhoff流和使用动态分离点得到

式中 η，E0——经 验 常 数（对 于NACA0015而言，η=1，E0=0.25）。

图2-16为通过Leishman Beddoes模型计算的法向力系数随攻角变化的结果。在图中，对于NACA0015而言，α=6+16sin（ωt），k=0.1，M=0.1，c=0.5m；k为衰减频率，M为马赫数，c为弦长。