双制动盘多流管理技术分析

1981年美国国家航空航天局（National Aeronautics and Space Administration，NASA）工程师ParaschivoiuⅠ为评估Darrieus风力机气动性能，提出了双制动盘多流管理论。该理论将风轮旋转域均分为上风向和下风向串联的制动盘，旋转域内的诱导速度可在上、下风向两个区域内分别求出，双制动盘多流管模型如图2-8所示。穿过旋转平面的流场被分为若干流管，在流管边界上的压力变化对附近流管中的动量平衡微不足道，因此每个流管中的气动计算可视为相对独立的。

图2-8　双制动盘多流管模型

每个流管中上下风向的流体速度不一致，并且在高度方向上有着风速廓线分布规律，在双制动盘多流管模型中，忽略气流中的湍流和阵风效应，只考虑风速的平均效应，因此风速分布具有二维效应，垂直轴风力机风场效果如图2-9所示。风速廓线分布规律表示为

式中 vi——竖直方向局部自由来流风速；

ve——赤道来流风速；

Zi——竖直方向参考高度；

ZEQ——风轮赤道圆位置高度；

αw——风速廓线因子。

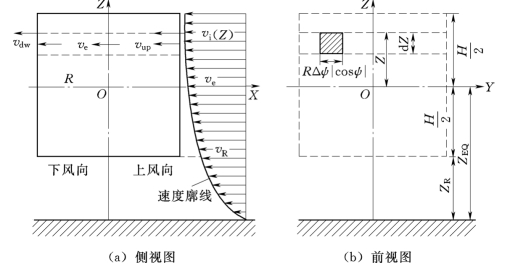
图2-9　垂直轴风力机风场效果

流管中的气流速度受到上下制动盘的作用，假设制动盘1处于上风向，在该制动盘内叶片旋转角度范围为（-π/2≤ψ≤π/2）；制动盘2处于下风向，在该制动盘内叶片旋转角度范围为（π/2≤ψ≤3π/2）。由于受到制动盘作用，流体速度沿流管逐渐减小，即下风向区域的气流诱导速度低于平衡速度区域的流速，而平衡速度区域流速低于上风向气流诱导速度，即

式中 vup，vdw——上风向、下风向气流诱导风速；

ve——平衡速度区域内诱导风速；

vw——尾流速度。(www.xing528.com)

根据诱导关系，存在如下关系

式中 μ——上风向区域诱导因子；

μ′——下风向区域诱导因子。

根据风轮方位角定义，上风向的叶片叶素的合成入流速度W和局部攻角α可定义为

其中　

而在下风向，叶素的合成入流速度W′和攻角α′由对应的局部坐标系中参数X′=rω/vdw和vdw代替。对于上风向区域，风轮的法向推力FN和切向力FT可表达为

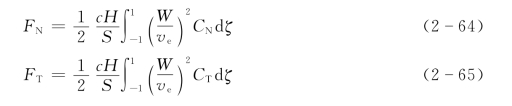
式中 H——风轮的高度；

S——风轮沿风向投影面积。

在下风向，其推力和切向力系数由对应坐标系参数表示。

在双制动盘多流管模型中，未考虑叶片的动态失速，因此风轮在上、下风向区域内其平均转矩系数可表示为

而风轮旋转一周内，功率输出系数是上下游转矩系数的加权，可表示为

式中 λEQ——风轮赤道半径位置的叶尖速比。