单流管模型的原理与应用分析

图2-3　单流管模型示意图

为计算叶片呈曲线分布的Darrieus风力机的气动性能，加拿大航空航天研究所（National Research Council-Institute for Aerospace Research，NRC-IAR）工程师R.J.Templin于1974年提出了基于动量定理的单盘面单流管模型。该模型将风力机的风轮简化为被一个流管包围的盘面，单流管模型示意如图2-3所示，假定盘面上叶片的诱导速度均匀分布，将所有叶片经过流管上游区域和下游区域的作用力合力作为该流管的外力，应用动量理论建立联系这一外力和流管内动量变化的方程式，从而求解诱导速度，然后推导风轮的气动性能。

单流管模型中引入了风轮形状参数，如叶片实度、径高比，风轮气动特性中的翼型升阻比被考虑其中，但是忽略了风剪切效应。

根据Glauert理论，通过风轮制动盘的速度vD是来流风速v和尾流速度vw的算术平均值，即

风力机风轮的运行阻力FD可表示为

基于动压和制动盘的面积，其阻力系数CFD为

将式（2-20）代入，可得

基于环境动压，对于风轮整机结构的阻力系数，可表述为

对于Φ型Darrieus风力机，其叶片型线通常为Troposkien曲线，采用径高比（截面旋转直径与高度比值），其型线又呈现抛物线分布，可表示为

式（2-24）可采用无因次形式表述，即

其中

式中 r——局部截面旋转半径；

z——距离风轮赤道平面的高度。

具有三叶片的Φ型Darrieus风力机如图2-4所示。对式（2-24）进行微分，可得到弯曲叶片局部倾角为(www.xing528.com)

图2-4　具有三叶片的Φ型Darrieus风力机

在单流管理论中，采用动量叶素理论进行风轮气动力计算时，需要确定叶素的局部气动攻角和局部相对动压。对叶素合成入射气流速度进行分解，可得上述两个参数的表达式为

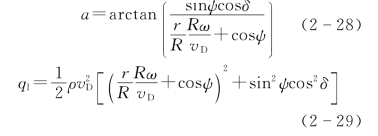
假设风轮在迎风面的方位角ψ范围为0°～180°，顺风面范围为180°～360°。在定常气流作用下，瞬时叶素的升力系数CL和阻力系数CD是关于攻角α的函数，法向力系数CN和切向力系数CT的计算公式为

弦长为c的叶素受到的法向微元力d N和前行推力d T可表述为

叶素的阻力可表示为

阻力的平均值可通过对风轮旋转一周（0≤ψ≤2π）和在高度范围（-H≤z≤H）二次积分获得。具有N个叶片、弦长为c的Φ型Darrieus风力机总阻力为

对于Φ型Darrieus风力机，其旋转制动盘为对称分布，可沿风轮赤道面进行分割，取上半部分积分求解，结果乘以2倍。并且抛物线叶片旋转形成的制动盘有效面积约为S=RH，因此，制动盘的阻力系数可表述为

风轮转矩仅由作用在叶素上的切向力分量产生，对于长度为d z/cosδ的单个叶素，其转矩可表示为

风轮的扭矩随着叶片的方位角和高度变化而改变，对前述两个变量（ψ，z）进行积分并乘以叶片个数可得风轮总扭矩为

进而风力机的输出功率可表示为