叶素理论及其在Φ型Darrieus风力机中的应用

叶素理论的基本出发点是将叶片沿叶展方向分成若干微段，称为叶素。该理论将叶素视为一个二维翼型，并假设作用在每个叶素上的力互不干扰。将叶素作为研究对象，分析各个叶素上所受的力和力矩，然后沿叶片展向积分，即可求得整个叶片上所受的气动力。本节以Φ型Darrieus风力机为研究对象，分析叶素理论及其应用。叶素理论应用如图2-2所示。取单位长度叶素，以叶素所处位置点O1为坐标原点，建立叶素随动坐标系O1mnt，如图2-2（a）所示。其中O1t是切向坐标轴，沿叶素翼型由尾缘指向前缘为正方向。O1m为沿叶片展向的切向方向，其正方向由右手坐标系法则确定。叶片展向切线方向与竖直方向的夹角称为叶片的倾角，记为。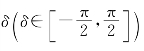

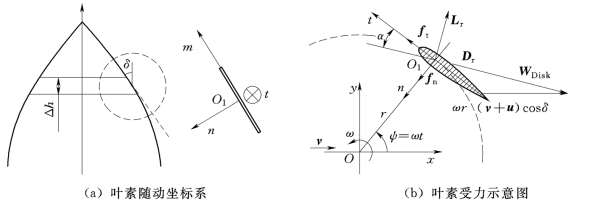
图2-2　叶素理论应用

当风力机以恒定角速度ω运转时，在风轮任意高度h处作一截面，得到半径为r的旋转圆，叶素受力示意图如图2-2（b）所示。首先以单个叶片运动为例，在来流风速v作用下，忽略垂直于风速方向（y向）的诱导速度，仅考虑平行于风向（x向）的诱导速度u，则旋转面上的合成速度为

将旋转面处速度记为

分析叶片受力，将式（2-7）沿叶素随动坐标系O1t和O1n轴方向分解，得到

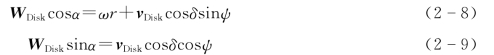
由式（2-8）、式（2-9）可得叶素的入射攻角和合成速度为

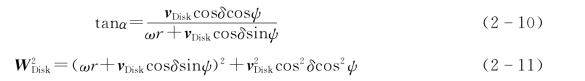
叶素在运转过程中，受到由于气流作用生成的升力Lr和阻力Dr，如图2-2（b）所示，将升力Lr和阻力Dr沿叶片切向和法向分解即可得到叶片的切向力ft和法向力fn，即

(www.xing528.com)

风力机风轮旋转时，实际只有叶片的切向力ft对中心转轴产生转矩，故风力机的转矩可表示为

在风轮截面坐标系Oxyz中，将叶片的切向力ft和法向力fn沿平行于风向和垂直于风向分解可以得到叶素的推力fx和侧向力fy为

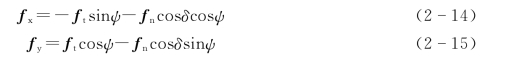
以上各式给出了单位长度叶素的受力情况，整根叶片的受力只需沿着叶展方向积分即可得到。设叶片长度为l，则有

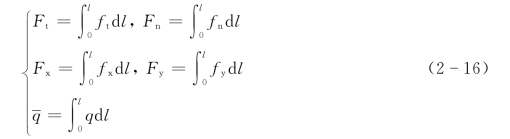
叶片旋转一周，其受力随风轮方位角改变而发生周期性变化，式（2-16）可以基本描述单根叶片的气动力分布。但是，为了研究整个风力机的气动性能及载荷分布，尚需要分析叶片旋转一周内的平均受力情况。

设风力机由N个叶片组成，则风轮的平均推力TFx、TFy、平均转矩Q和平均功率P可表示为

将上述物理量进行无量纲形式表述有利于分析叶片的运动状态及比较机型的优劣，式（2-17）的无因次化可表示为

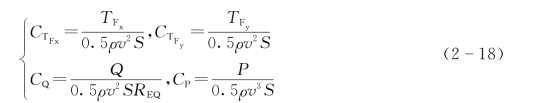
式中 REQ——风轮赤道圆处的半径。