热电偶测温的基本原理

1.热电效应

将两种不同金属导体A、B连成闭合回路，且两节点的温度T、T₀不同，则回路中将有电动势产生，而在回路中就会有一定大小的电流，这种现象叫做热电效应，回路内的电动势称为热电动势，简称热电势，如图7-1所示。

通常，把上述两种不同导体的组合称为热电偶，称A、B两导体为热电极。两个接点，一个为工作端或热端（T），测量时将它置于被测温度场中；另一个叫自由端或冷端（T₀），一般要求恒定在某一温度。在图7-1所示的热电偶回路中，热电偶所产生的热电动势由两部分组成：接触电动势和温差电动势。

接触电动势产生的原因为：两金属导体A、B内电子密度n_A、n_B不同，当A、B形成节点时，由于节点两侧存在电子密度差而发生电子扩散，使一侧失去电子带正电荷，另一侧得到电子带负电荷，最终节点两侧形成稳定的电动势。这个电动势是由于不同金属接触而形成的，所以很形象地把它称为接触电动势。回路内各节点形成的接触电动势共同构成热电偶的热电动势。

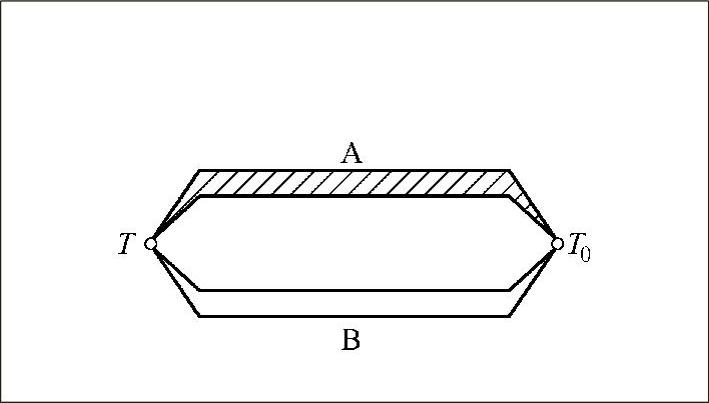
图7-1 热电偶的结构示意图

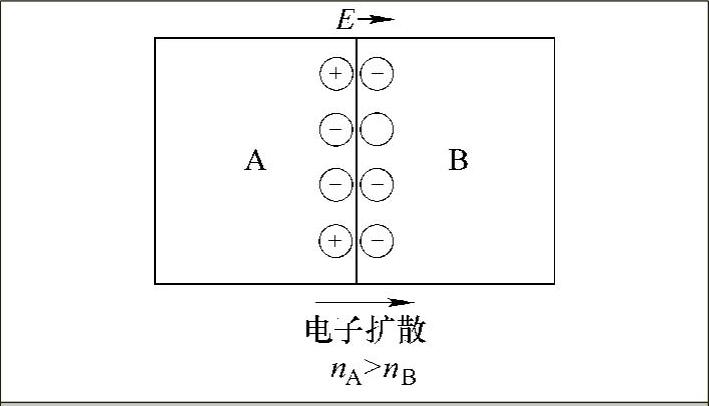
图7-2 两不同导体接触处电子的扩散与静电场的形成

设导体A的自由电子密度大于导体B的自由电子密度（n_A＞n_B），那么在单位时间内，由导体A扩散到导体B的电子数要比导体B扩散到导体A的电子数多。这时导体A因失去电子而带正电，导体B因得到电子而带负电。于是在接触表面上便形成了一个电场，在A、B之间形成一个电位差，即电动势，如图7-2所示。

这个电动势将阻碍电子由导体A向导体B的进一步扩散。当电子的扩散作用与阻碍扩散的作用相等时，接触处的自由电子的扩散便达到动态平衡。这种由于两种导体自由电子密度不同，而在其接触处形成的电动势，称为接触电动势。用符号E_AB（T）和E_AB（T₀）表示导体A和导体B的两处接触点在温度T和T₀时形成的电位差。根据物理学上的推导，有

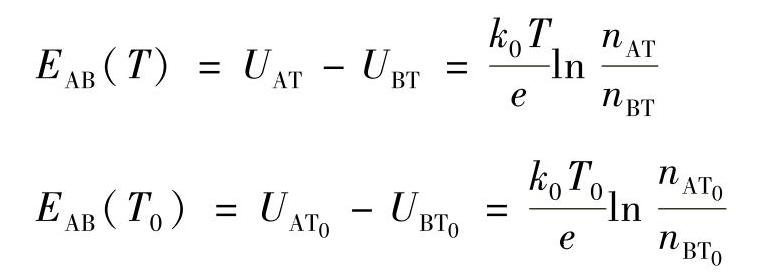
式中 k₀——波兹曼常数，k₀=1.38×10^-23J/K=8.62×10^-5eV/K；

T、T₀——热电偶接触处（节点）的绝对温度（K）；

n_A、n_B——材料A、B的自由电子密度；

e——电子电荷量，e=1.602×10^-19C；

E——回路中的电动势。

热电偶热电动势的另一个组成部分是温差电动势。温差电动势是在同一导体的两端因其温度不同而产生的一种热电动势。实验与理论均已证明，热电偶回路总电动势主要是由接触电动势引起的。在图7-1中，若A为正极，B为负极，则所产生的总电动势为

E_AB（T，T₀）=E_AB（T）-E_AB（T₀）

在图7-1中所示热电偶的热电动势近似为

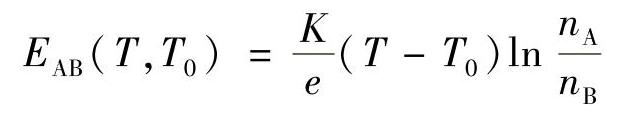
两金属的电子密度近似为常数，所以由式可得：热电偶的热电动势E_AB（T，T₀）与热电偶两节点的温度差（T，T₀）成正比。

若令温度T₀已知且固定，将热电偶的热端置于待测温度中，即令T等于待测温度，则通过测量热电偶的热电动势即可实现待测温度T的测量。这就是热电偶测温的基本原理。

2.热电偶基本定律

由式可知：

1）只有由不同导体组成的热电偶，其两节点的温度不同时，回路中才有热电动势产生。热电动势的大小只与两热电极材料的性质及两节点的温度有关，而与热电极的形状、大小无关。若热电偶两电极材料相同，则无论两接点温度如何，总热电动势为零。若热电偶两接点温度相同，尽管A、B材料不同，回路中总电动势等于零。

2）中间导体定律。在热电偶中插入第三种材料，只要插入材料两端的温度相同，对热电偶的总热电动势没有影响。

在A、B材料组成的热电偶回路中接入第三导体C，只要引入的第三导体两端温度相同，则此导体的引入不会改变总电动势E_AB（T，T₀）的大小。在实际应用中，热电偶回路中需接入测量仪表，相当于在热电偶回路中接入第三导体，如图7-3所示。(www.xing528.com)

在图7-3a中，2、3两点温度相同，回路中总电动势

E_ABC（T，T0）=E_AB（T）+E_BC（T₀）+E_CA（T₀）

当回路中各接点温度相同时，总电动势为零，即

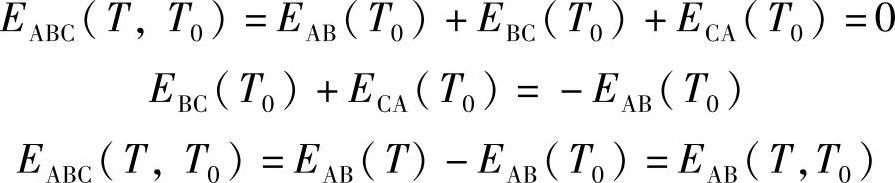
同理可证图7-3b所示的情况。

标准热电极法：如果两种导体（A和B）分别与第三种导体（C）组成热电偶所产生的热电动势已知，则由这两个导体（A，B）组成的热电偶产生的热电动势可由下式算得：

E_AB（T，T₀）=E_AC（T，T₀）-E_BC（T，T₀）

如图7-4所示，AC、BC、AB为三个热电偶，工作端温度为T，冷端温度为T₀，则

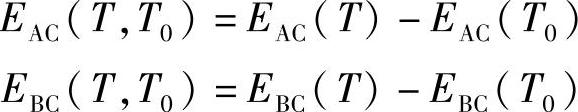
将上两式相减得

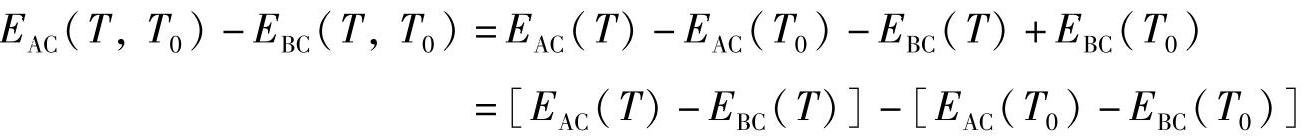
由式有。

热电偶回路中插入多种导体后，只要保证插入的每种导体的两端温度相同，就对热电偶的热电动势没影响。根据这个定律，可以将连接导线和显示仪表看成中间导体，只要保证中间导体两端温度相同，则对热电偶的热电动势没有影响。

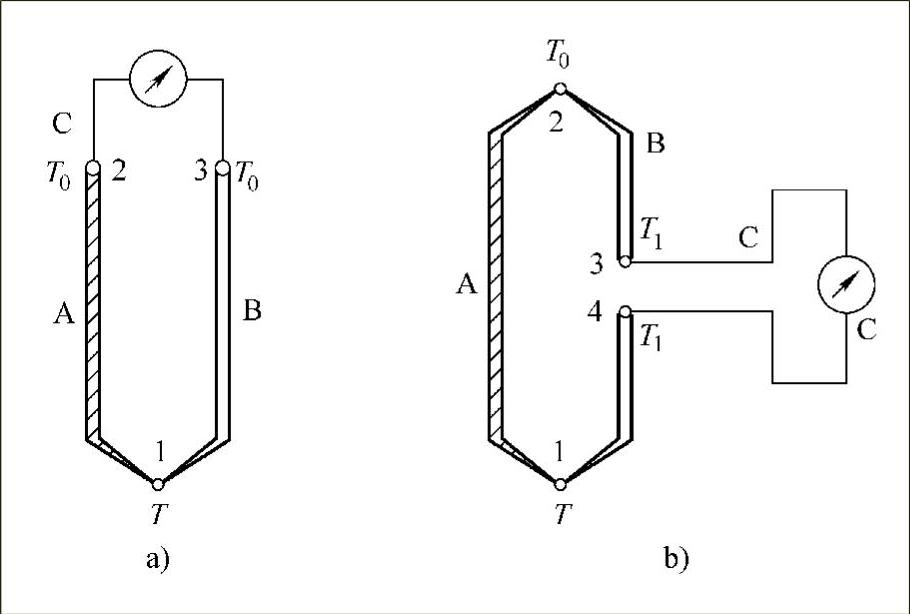
图7-3 热电偶回路中引入第三导体

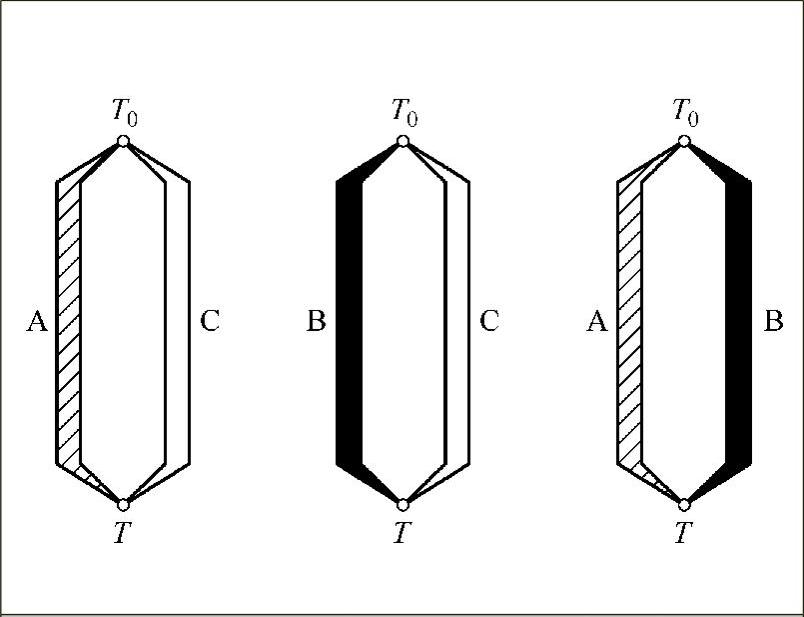
图7-4 通过标准热电极C求组合热电偶的热电动势

3）中间温度定律。热电偶两节点温度为（T，T₀）时的电动势E_AB（T，T₀）等于该热电偶在节点温度为（T，T_n）及（T_n，T₀）时的热电动势E_AB（T，T_n）与E_AB（T_n，T₀）之和，T_n称为中间温度。热电偶中间温度定律的测量回路如图7-5所示。该定律可用下式表示，即

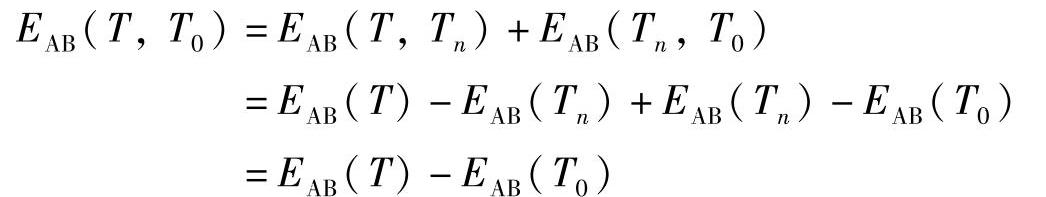
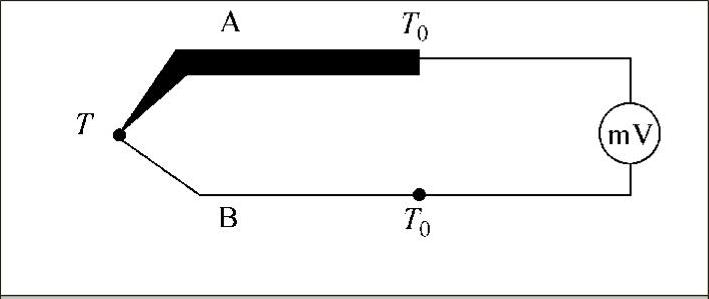
图7-5 热电偶测量回路

4）当热电极A、B选定后，热电动势E_AB（T，T₀）是两接点温度T和T₀的函数差，即

E_AB（T，T₀）=f（T）-f（T₀）

如果使冷端温度T₀保持不变，则f（T₀）=C（常数）。此时，E_AB（T，T₀）就成为T的单值函数，即

E_AB（T，T₀）=f（T）-C=ϕ（T）