电涡流式传感器的工作原理和应用

电涡流式传感器是利用电涡流效应将位移等非电被测参量转换为线圈的电感或阻抗变化的变磁阻式传感器。电涡流式传感器的敏感元件是线圈，当给线圈通以交变电流并使它接近金属导体时，线圈产生的磁场就会被导体电涡流产生的磁场部分抵消，使线圈的电感量、阻抗和品质因数发生变化。

1.工作原理

当金属导体放置在变化的磁场或在磁场中运动时，导体内就会产生感应电流，这种电流就像水中旋涡那样在导体内转圈，称之为电涡流或涡流，这种现象就称为涡流效应。

根据法拉第定律，当传感器线圈通以正弦交变电流I₁时，由于电流的变化，在线圈周围空间必然产生正弦交变磁场H₁，使置于此磁场中的金属导体中感应电涡流I₂，I₂又产生新的交变磁场H₂。根据楞次定律，H₂的作用将反抗原磁场H₁，由于磁场H₂的作用，涡流要消耗一部分能量，导致传感器线圈的等效阻抗、品质因数和电感量发生变化。由上可知，线圈阻抗的变化完全取决于被测金属导体的电涡流效应。

电涡流效应既与被测体的电阻率ρ、磁导率_μ以及几何形状有关，还与线圈的几何参数、线圈中励磁电流频率f有关，同时还与线圈和导体间的距离x有关。因此，传感器线圈受电涡流影响时的等效阻抗Z的函数关系式为

Z=F（ρ，μ，r，f，x）

式中 r——线圈与被测体的尺寸因子。

如果保持上式中其他参数不变，而只改变其中一个参数，就可以构成测量该参数的传感器。改变线圈和导体之间的距离，可以制作成测量位移、厚度、振动的传感器；改变导体的电阻率，可以制作成测量表面温度、检测材质的传感器；改变导体的磁导率，可以制作成测量应力、硬度的传感器。传感器线圈阻抗Z就仅仅是这个参数的单值函数。通过与传感器配用的测量电路测出阻抗Z的变化量，即可实现对该参数的测量。

电涡流式传感器可以看成由一个载流线圈和金属导体两部分组成，如图3-17所示。

2.基本特性

电涡流传感器简化模型如图3-18所示。模型中，把在被测金属导体上形成的电涡流等效成一个短路环，即假设电涡流仅分布在环体之内，模型中h（电涡流的贯穿深度）可由下式求得

式中 f——线圈励磁电流的频率。

根据简化模型，可画出如图3-19所示的等效电路图。图中，R₂为电涡流短路环等效电阻，其表达式为

根据基尔霍夫第二定律，可列出如下方程：

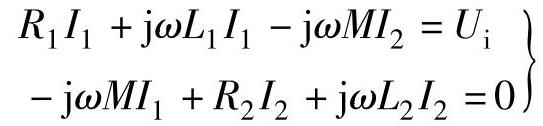
式中 ω——线圈激磁电流角频率；

R₁、L₁——导电线圈电阻和电感；

L₂——短路环等效电感；

R₂——短路环等效电阻；

M——互感系数。

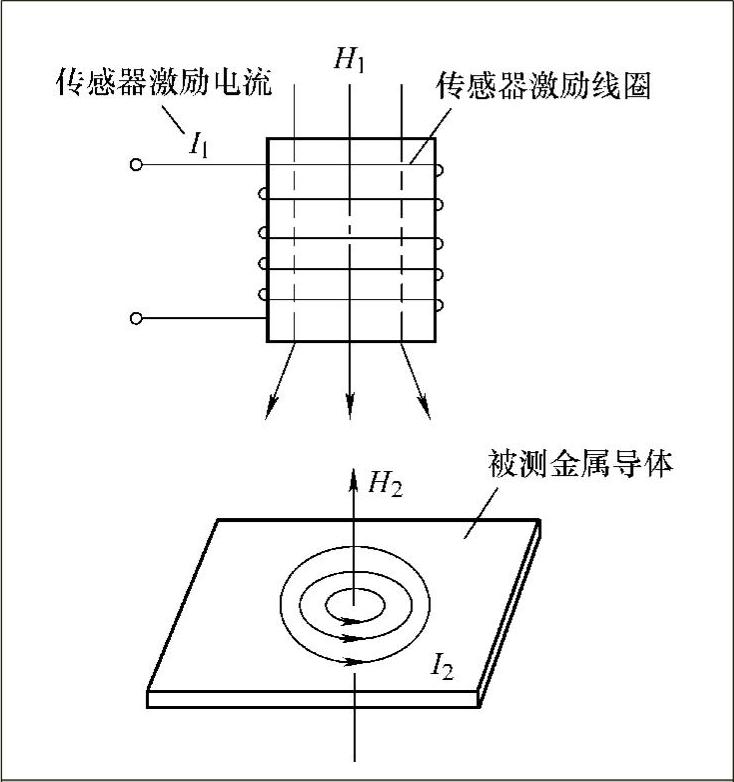
图3-17 电涡流式传感器

图3-18 电涡流式传感器简化模型

1—传感器线圈 2—短路环 3—被测金属导体

解得等效阻抗Z的表达式为

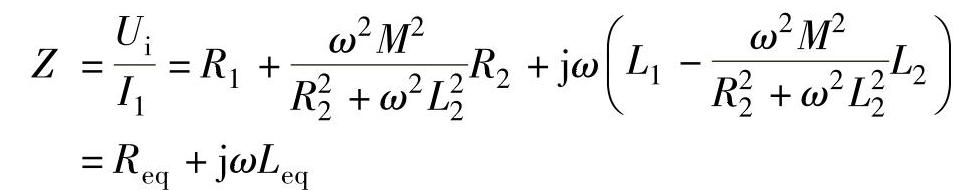
式中 R_eq——线圈受电涡流影响后的等效电阻，。

L_eq——线圈受电涡流影响后的等效电感，。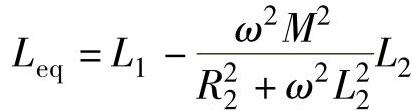

L₁——不计电涡流效应时线圈电感；

L₂——电涡流等效电路的等效电感。

线圈的等效品质因数Q值为

综上所述，根据电涡流式传感器的简化模型和等效电路，运用电路分析的基本方法得到的参数，为电涡流式传感器基本特性表示式。在某一范围内，可以将这些函数关系近似地通过某一线性函数来近似，电涡流式传感器不是在电涡流整个波及范围内都能呈线性变化的。

3.电涡流形成范围

（1）电涡流的径向形成范围(www.xing528.com)

线圈—导体系统产生的电涡流密度既是线圈与导体间距离x的函数，又是沿线圈半径方向r的函数。当x一定时，电涡流密度J与半径r的关系曲线如图3-20所示（图中J₀为金属导体表面电涡流密度，即电涡流密度最大值。J_r为半径r处的金属导体表面电涡流密度）。由图可知：

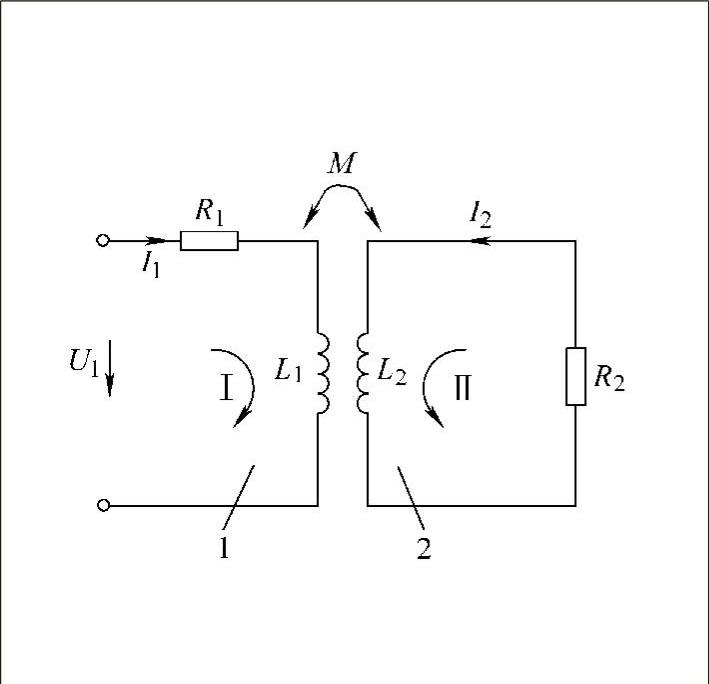
图3-19 电涡流式传感器等效电路图

1—传感器线圈 2—电涡流短路环

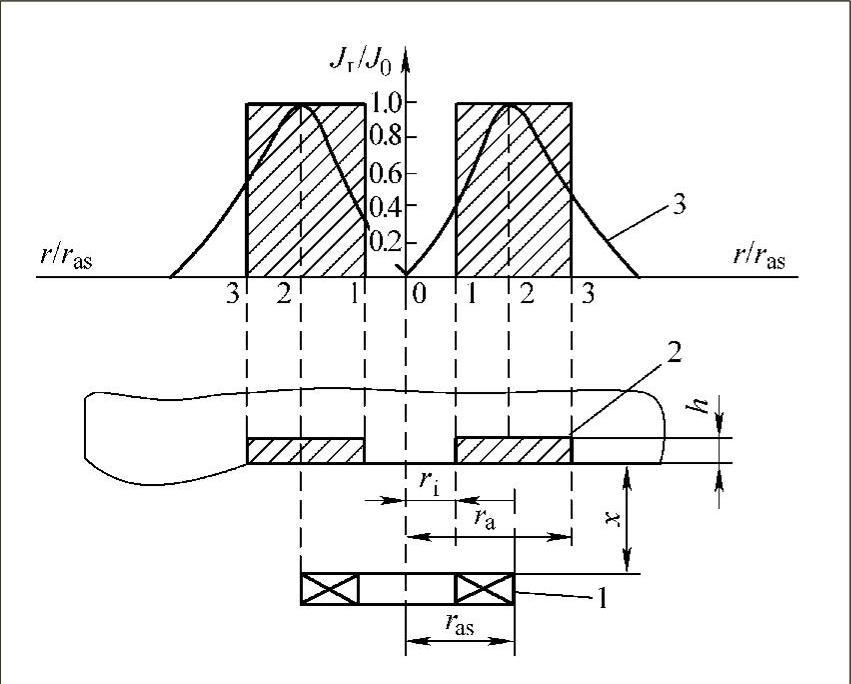
图3-20 电涡流密度J与半径r的关系曲线

1—电涡流线圈 2—等效短路环 3—电涡流密度分布

1）电涡流径向形成范围大约在传感器线圈外径r_as的1.8～2.5倍范围内，且分布不均匀。

2）电涡流密度在r_i=0处为零。

3）电涡流的最大值在r=r_as附近的一个狭窄区域内。

4）可以用一个平均半径为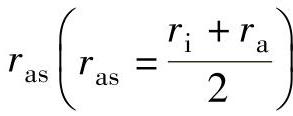的短路环来集中表示分散的电涡流（图中阴影部分）。

（2）电涡流强度与距离的关系

理论分析和实验都已证明，当x改变时，电涡流密度也发生变化，即电涡流强度随距离x的变化而变化。根据线圈-导体系统的电磁作用，可以得到金属导体表面的电涡流强度为

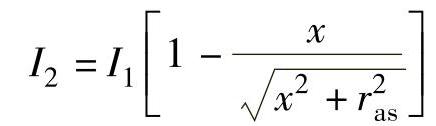
式中 I₁——线圈激励电流；

I₂——金属导体中等效电流；

x——线圈到金属导体表面距离；

r_as——线圈外径。

根据上式做出的归一化曲线如图3-21所示。

以上分析表明：

1）电涡流强度与距离x呈非线性关系，且随着x/r_as的增加而迅速减小。

2）当利用电涡流式传感器测量位移时，只有在x/r_as＜＜1（一般取0.05～0.15）的条件下才能得到较好的线性和较高的灵敏度。

（3）电涡流的轴向贯穿深度

所谓贯穿深度，是指把电涡流强度减小到表面强度的1/e处的表面厚度。

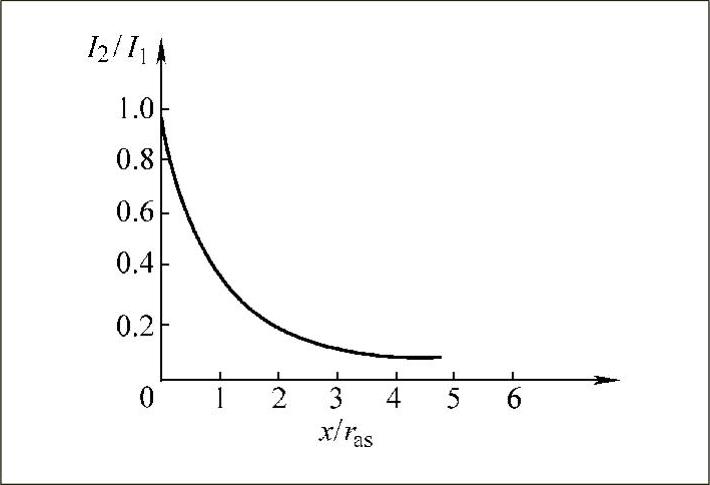
图3-21 电涡流强度与距离归一化曲线

由于金属导体的趋肤效应，电磁场不能穿过导体的无限厚度，仅作用于表面薄层和一定的径向范围内，并且导体中产生的电涡流强度是随导体厚度的增加按指数规律下降的。其按指数衰减分布规律可用下式表示：

J_d=J₀e-d/h

式中 d——金属导体中某一点与表面的距离；

J_d——沿H₁轴向d处的电涡流密度；

J₀——金属导体表面电涡流密度，即电涡流密度最大值；

h——电涡流轴向贯穿的深度（趋肤深度）。

图3-22所示为电涡流密度轴向分布曲线。由图可见，电涡流密度主要分布在表面附近。

由前面分析所得式可知，被测体电阻率越大，相对磁导率越小，以及传感器线圈的励磁电流频率越低，则电涡流贯穿深度h越大。故透射式电涡流式传感器一般都采用低频激励。

图3-22 电涡流密度轴向分布曲线