变气隙式电感传感器的工作原理和应用场景

1.变气隙式电感传感器工作原理

图3-3所示为最简单的变气隙式电感传感器结构原理图。根据电磁学知识，得到变气隙式电感传感器的基本工作原理。

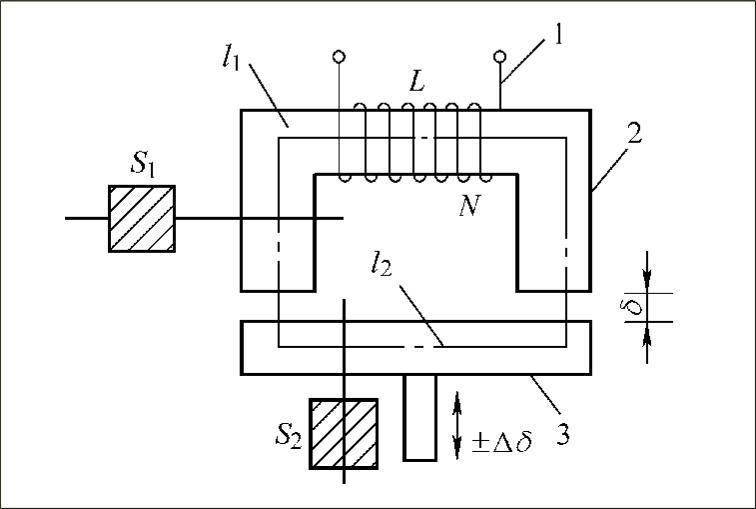
图3-3 变气隙式电感传感器

1—线圈 2—铁芯（定铁芯 3—衔铁（动铁芯）

衔铁和铁芯之间有空气隙，气隙厚度为δ。传感器的运动部分与衔铁相连，工作时衔铁与被测物体接触。当衔铁移动时，气隙厚度δ发生改变，引起磁路中气隙的磁阻变化，从而引起线圈电感变化，这种电感量的变化与衔铁位置（气隙大小）相对应。传感器线圈与测量电路连接后，将检测到的电感量的变化转化成电压、电流或频率的变化，完成从非电量到电量的转换，就能判断衔铁位移量的大小和方向。

根据对电感的定义，线圈中电感量可由下式确定：

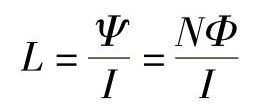
式中 Ψ——线圈总磁链；

I——通过线圈的电流；

N——线圈的匝数；

Φ——穿过线圈的磁通。

由磁路欧姆定律，得

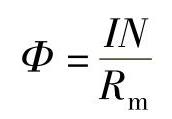
式中 R_m——磁路总磁阻。

根据电感的定义，线圈自感为

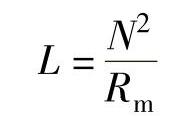
式中 R_m——磁路总磁阻；

N——电感传感器线圈的匝数。

由于变气隙式电感传感器的气隙通常较小，可以认为气隙间磁场是均匀的，磁路是封闭的，因此可忽略磁路损失。总磁阻为

R_m=R_m0+R_m1+R_m2

对于变气隙式传感器，若忽略磁路磁损，则磁路总磁阻为

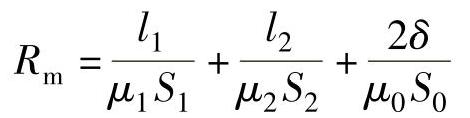
式中 μ₁——铁芯材料的磁导率；

μ₂——衔铁材料的磁导率；

l₁——磁通通过铁芯的长度；

l₂——磁通通过衔铁的长度；

S₁——铁芯的截面积；

S₂——衔铁的截面积；

μ₀——空气的磁导率；

S₀——气隙的截面积；

δ——气隙的厚度。

由于导磁体的磁导率远远大于空气的磁导率，即μ₁＞＞μ₀和μ₂＞＞μ₀，所以通常气隙磁阻远大于铁芯和衔铁的磁阻，即

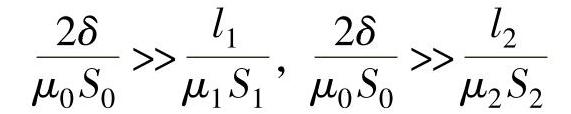
则磁路总磁阻可写为

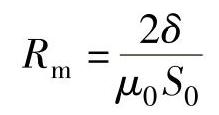(https://www.xing528.com)

通过各公式转换可得自感量为

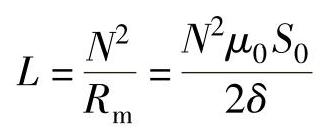
上式表明，当线圈匝数为常数时，电感L仅仅是磁路中磁阻R_m的函数，改变δ或S₀均可导致电感变化，因此变磁阻式传感器又可分为变气隙厚度δ的传感器和变气隙面积S₀的传感器。目前使用最广泛的是变气隙厚度式电感传感器。

电感线圈结构确定后，电感与面积成正比，与气隙长度成反比。这样，只要被测量能引起面积和气隙的变化，都可用电感传感器进行测量。其灵敏度为

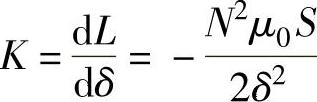
为提高灵敏度并保证一定的线性度，变气隙式电感传感器只能工作在很小的区域，因而只能用于微小位移的测量。

2.输出特性

在线圈匝数N确定后，如保持气隙有效截面积为常数，则由电感量L公式可知L与δ之间是非线性关系。特性曲线如图3-4所示。设电感传感器初始气隙为δ₀，初始电感量为L₀，衔铁位移引起的气隙变化量为Δδ，当衔铁处于初始位置时，初始电感量为

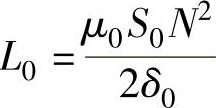
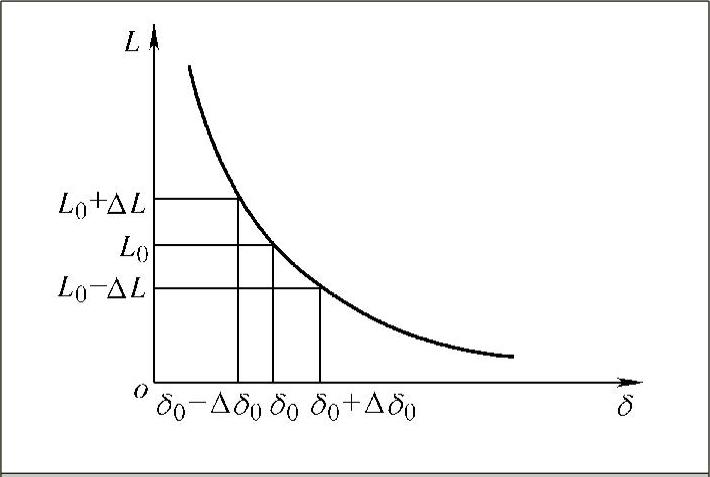
图3-4 变气隙式电感传感器的L-δ特性

当衔铁上移Δδ时，传感器气隙减少Δδ，即δ=δ₀-Δδ，则此时输出电感为L=L₀+ΔL，代入公式并整理，得

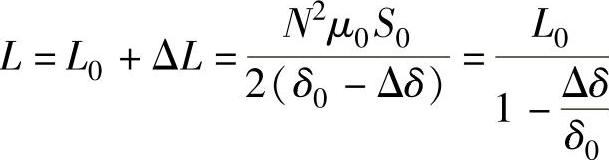
当Δδ/δ₀＜＜1时，可将上式用泰勒级数展开成如下的级数形式：

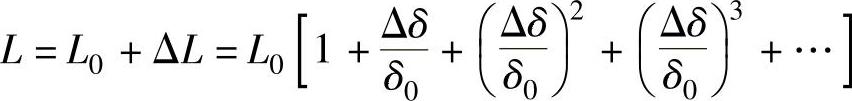
由上式可求得电感增量ΔL和相对增量ΔL/L₀的表达式，即

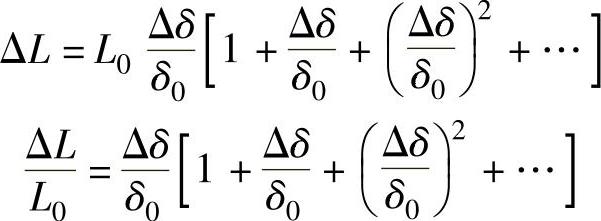
同理，当衔铁随被测体的初始位置向下移动Δδ时，有

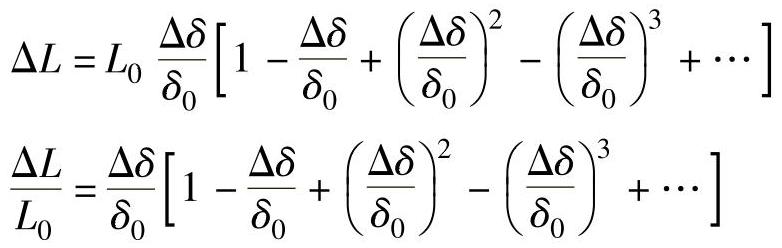
对公式做线性处理，即忽略高次项后，可得

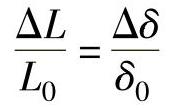
当衔铁受到外力的作用，使气隙变大时，电感的相对变化量为

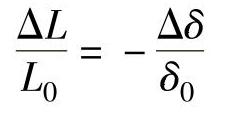
灵敏度为

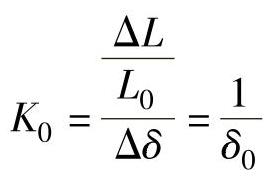
为了保证一定的线性度，变气隙式电感传感器仅能工作在很小一段区域内，因而能用于

微小位移的测量，一般取δ₀=0.1～0.5mm，Δδ=0.1～0.2δ₀。

由此可见，变气隙式电感传感器的测量范围与灵敏度及线性度相矛盾，因此变气隙式电感传感器适用于测量微小位移的场合。为了减少非线性误差，实际测量中广泛采用差动变气隙式电感传感器，如图3-5所示。

差动变气隙式电感传感器由两个相同的电感线圈的磁路组成。测量时，衔铁与被测物体相连，当被测物体上下移动时，带动衔铁以相同的位移上下移动，两个磁回路的磁阻发生大小相等、方向相反的变化，一个线圈的电感量增加，另一个线圈的电感量减少，形成差动形式。

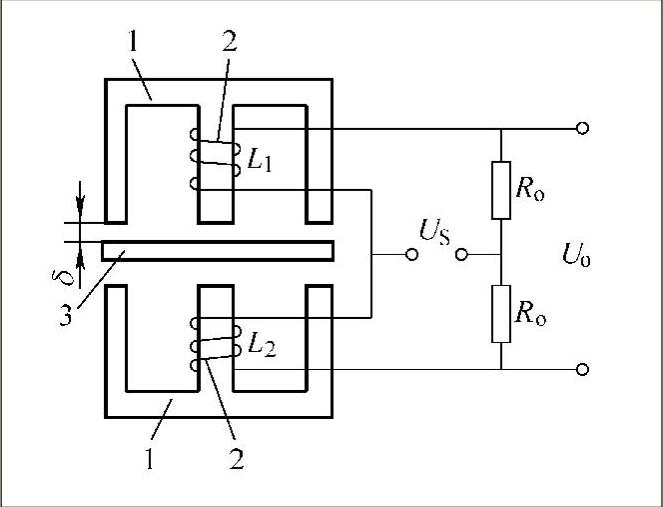
图3-5 差动变气隙式电感传感器

1—铁芯 2—线圈 3—衔铁

将两个电感线圈接入交流电桥的相邻桥臂，另两个桥臂由电阻组成，电桥的输出电压与电感变化量ΔL有关，可得灵敏度为

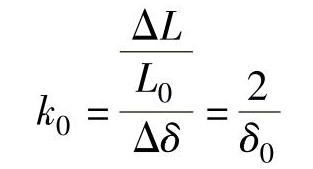
差动变气隙式电感传感器灵敏度较高，线性度好，差动式的两个电感结构可抵消温度、噪声干扰的影响。