积分和微分运算电路优化方案

在自控系统中，常用积分电路和微分电路作为电路环节，在仪器仪表之中它们还广泛用于波形的产生和变换；积分运算和微分运算互为逆运算。

7.1.4.1　积分运算电路

积分运算电路如图7.1.13所示，集成运放的同相输入端通过R′接地，PN0 uu==，为“虚地”。 电路中，电容C中电流等于电阻R中电流，即

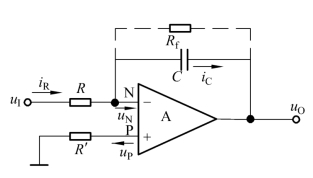
图7.1.13　积分运算电路

假设电容初始电压为零，由于电容上的电流为充电电流，电容电压为输出电压，故

由此得

1

t到2t时间段的积分值为

式中，uO(t1)为积分起始时刻的输出电压，即积分运算的起始值，积分的终值是t2时刻的电压。

当uI为常量时，输出电压为

积分电路的应用十分广泛，如图7.1.14所示为当输入为阶跃信号、方波信号、正弦波信号时输出的电压波形。

图7.1.14　积分运算电路在不同输入情况下的波形

在实用电路中，因为偏置电流、失调电压、失调电流及温漂不等于零，开环电压放大倍数、输入电阻及带宽不是无穷大，实际的电容器存在吸附效应和漏电阻等，因此实际积分电路的输出电压与输入电压的函数关系与理想情况相比存在误差，情况严重时甚至不能正常工作。为了防止低频信号增益过大，常在电容上并联一个反馈电阻加以限制，如图7.1.13中虚线所示。

7.1.4.2　微分运算电路

1.基本微分运算电路

若将图7.1.13所示电路中电阻R和电容C的位置互换，并选取比较小的时间常数RC，则得到基本微分运算电路，如图7.1.15所示。

图7.1.15　基本微分运算电路

根据“虚短”“虚断”的原则有uP=uN=0，所以电容两端电压uC=uI，因而有

由此可得输出电压为

即输出电压正比于输入电压对时间的微分。(www.xing528.com)

2.实用微分运算电路

图7.1.15所示基本微分电路存在以下问题：由于输出电压与输入电压的变化率成正比，因此输出受输入影响较大；当受到大幅值脉冲干扰时，会因为充电电流变化过大而使集成运放内部的放大管进入饱和或截止状态，使得电路不能正常工作；由于反馈网络为滞后环节，它与集成运放内部的滞后环节相叠加，易于满足自激振荡的条件，从而使电路不稳定。

为了解决上述问题，可以在输入端串联一个小阻值的电阻R1，以限制输入电流，即限制了R中电流；在反馈电阻R上并联稳压二极管，以限制输出电压幅值，保证集成运放中的放大管始终工作在放大区，不至于出现阻塞现象；在R上并联小容量电容C1，起相位补偿作用，提高电路的稳定性；如图7.1.16（a）所示。该电路的输出电压与输入电压成近似微分关系。若输入电压为方波且RC≪T/2（T为方波的周期），则输出为尖顶波，如图7.1.16（b）所示。

图7.1.16　实用微分运算电路

（1）逆函数型微分运算电路。

因为微分运算和积分运算互为逆运算，若将积分运算电路作为反馈电路，则可得到微分运算电路，如图7.1.17所示。为了保证电路引入的是负反馈，应使输出电压uO2与输入电压uI极性相反，uI应加在A1的同相输入端。

在图7.1.17所示电路中有i1=i2，即

图7.1.17　逆函数型微分运算电路

根据积分运算电路的运算关系可知

因此

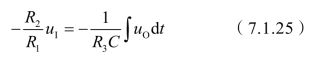
从而得到输出电压的表达式为

利用逆函数运算实现运算电路具有实用价值。例如，采用乘法运算电路作为集成运放的反馈通路，便可以实现除法运算；采用乘方运算电路作为集成运放的反馈通路，便可以实现开方运算，等等。需要注意的是，与一般运算一样，利用逆运算的方法组成运算电路时，引入的必须是负反馈。在自动控制系统中，积分运算常用来提高调节精度，而微分运算则用来加速过渡过程。

例7.1.2　电路如图7.1.18所示，C1=C2=C，试求出uO与uI的运算关系式。

解：根据“虚短”和“虚断”的原则，在节点N上，电流方程为

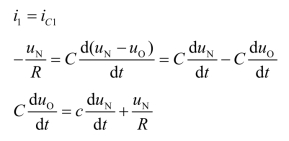
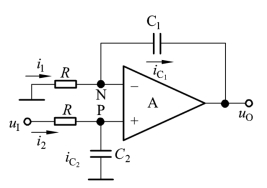
图7.1.18　例7.1.2的电路图

在节点P上，电流方程为

因为uP=uN，所以

在t1～t2时间段中，uO的表达式为

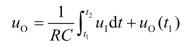
电路实现了同相积分运算。