加减运算电路的设计与应用

加减运算电路一般是在比例运算电路的基础上实现多个输入信号各不同比例求和或求差的电路。所有输入在同一个输入端的可以实现加法运算，在不同输入端的实现减法运算，分析的方法为节点电流法和叠加原理，这里选用叠加原理进行分析。

7.1.3.1　求和运算电路

1.反相求和运算电路

反相求和运算电路的多个输入信号均作用于集成运放的反相输入端，如图7.1.6所示。对于多输入的电路，除了用节点电流法求解运算关系外，还可以利用叠加原理，首先分别求出各输入电压单独作用时的输出电压，然后将它们相加，便得到所有信号共同作用时输出电压与输入电压的运算关系。

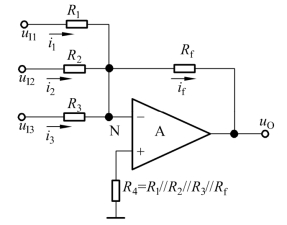
图7.1.6　反相求和运算电路

图7.1.7　利用叠加原理求解运算关系

设uI1单独作用，此时应将uI2和uI3接地，如图7.1.7所示。由于电阻R2和R3的一端是“地”，一端是“虚地”，故它们的电流为零。因此，电路实现的是反相比例运算，有

利用同样的方法，分别求出uI2和uI3单独作用时的输出uO2和uO3，即

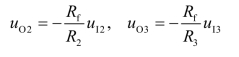
当uI1、uI2和uI3同时作用时，有

从反相求和运算电路的分析可知，各信号源为运算电路提供的输入电流各不相同，表明从不同的输入端看进去的等效电阻不同，即输入电阻不同。

2.同相求和运算电路

当多个输入信号同时作用于集成运放的同相输入端时，就构成同相求和运算电路，如图7.1.8所示。

图7.1.8　同相加法运算电路

在同相比例运算电路的分析中，曾得到式（7.1.6）所示的结论。因此求解uP，即可得到输出电压与输入电压的运算关系。

节点P的电流方程为

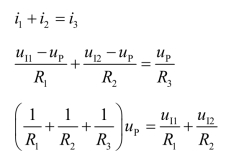
所以同相输入端电位为

式中，RP=R1//R2//R3。

将式（7.1.9）代入式（7.1.6）得

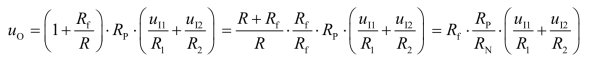
式中，RN=R//Rf。若RN=RP，则

若R//Rf=R1//R2，可省去R3。

利用叠加原理求解同相求和运算电路的uP可得(www.xing528.com)

输出电压为

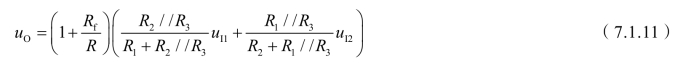
从上式中可以看出，虽叠加原理物理意义非常明确，但计算过程烦琐。

7.1.3.2　加减运算电路

从式（7.1.8）和式（7.1.10）可以看出，当输入电压作用在不同的输入端时就可以组成加减法运算电路，如图7.1.9所示为4个输入的加减运算电路。

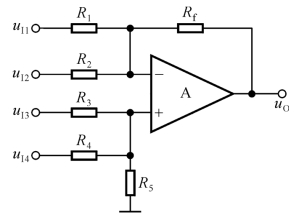
图7.1.9　加减法运算电路

首先将同相输入端的两个输入电压与地短路，如图7.1.10（a）所示，可以得到反相求和运算电路，得输出电压为

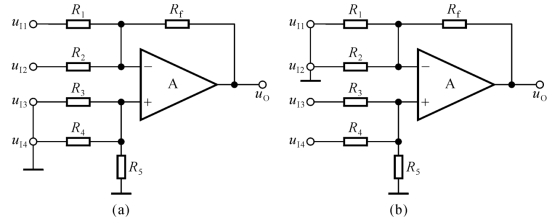
图7.1.10　利用叠加原理求解加减运算电路

再将反相端的两个电压输入端与地短路，如图7.1.10（b）所示，则得到同相求和电路，若R1//R2//Rf=R3//R4//R5，则输出电压为

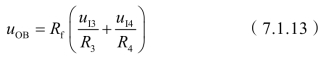
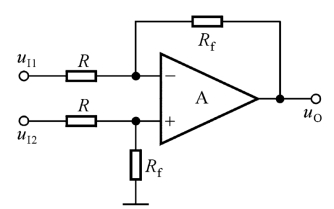
图7.1.11　差分比例运算电路

根据叠加原理，输出电压为

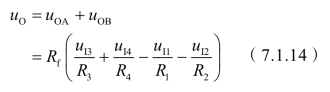
若电路只有两个输入且参数如图7.1.11所示，则

电路实现了对输入差模信号的比例运算。

使用单个集成运放构成加减运算电路时存在两个缺点：一是电阻的选取和调整不方便，二是对每个信号源而言输入电阻都较小。因此，必要时可采用两级电路。例如，可用图7.1.12所示电路实现差分比例运算，第一级电路为同相比例运算电路，第二级为差分比例运算电路。由图可得

根据叠加原理，第二级电路的输出为

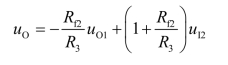
图7.1.12　高输入电阻的差分比例运算电路

若R1=Rf2，R3=Rf1，则有

从电路来看，第一个为同相比例运算电路，第二个为差分比例运算电路，输入电阻都为无穷大。