BJT高频小信号模型优化

4.4.1.1　BJT的高频小信号模型

在2.3.3节中讨论了BJT的低频小信号模型，但在高频小信号条件下，必须考虑BJT的发射结电容和集电结电容的影响，由此可得到BJT的高频小信号模型，如图4.4.1（a）所示。现就此模型中的各元件参数作简要说明。

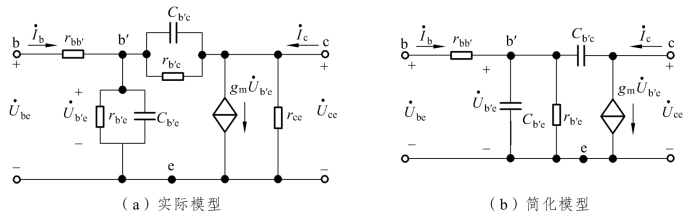
图4.4.1　BJT的高频小信号模型

1.基区体电阻rbb′

图中b′是为分析方便而虚拟的基区内的等效基极，rbb′表示基区体电阻。不同类型的BJT，rbb′的值相差很大，器件手册中给出的rbb′值在几十至几百欧之间。

2.电阻rb′e和电容Cb′e

rb′e是发射结正偏电阻re折算到基极回路的等效电阻，即rb′e= （1+β）re= （1+β）UT/IEQ。Cb′e是发射结电容，由于BJT在放大区时发射结正偏，所以Cb′e主要是扩散电容，数值较大，对于小功率管，Cb′e在几十至几百皮法范围。

3.集电结电阻rb′c和电容Cb′c

在放大区内，集电结处于反向偏置，因此rb′c的值很大，一般在100 kΩ～10 MΩ范围内。Cb′c主要是势垒电容，数值较小，在2～10 pF范围内。

4.受控电流源

由图4.4.1（a）可见，由于结电容的影响，BJT中受控电流源不再完全受控于基极电流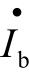，因而不能再用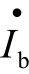β表示。BJT工作在放大区时，3个电极的电流实质上均受控于发射结上所加的电压，因而在高频小信号模型中，受控电流源改用受控制的电流源表示，这里的互导gm表明发射结电压对受控电流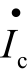的控制能力，定义为

对于高频小功率的BJT，gm约为几十毫西。gm与信号的频率无关。

由上述各元件的参数可知，rb′c的数值很大，在高频时远大于1/（ωCb′c），与Cb′c并联可视为开路；另外，rce与负载电阻RL相比，一般有rce＞RL，因此rce也可视为开路，这样便可得到图4.4.1（b）所示的简化模型。因其形状像π，各元件参数具有不同的量纲，故又称之为BJT的混合π形高频小信号模型。

4.4.1.2　BJT高频小信号模型中元件参数值的获得

由于BJT高频小信号模型中电阻等元件的参数值在很宽的频率范围内（f＜fT/3，fT是BJT的特征频率）与频率无关，而且在低频情况下，电容Cb′e和Cb′c可视为开路，于是图4.4.1（b）所示的简化模型可变为图4.4.2（a）的形式，它与图4.4.1（b）所示的H参数低频小信号模型一样，所以可以由BJT的低频小信号模型获得混合π形小信号模型中的一些参数值。

图4.4.2　BJT两种模型在低频时的比较

比较图4.4.2所示的两个模型，可得以下关系：

输入回路有

而

需要说明的是，式（4.4.2）中的β0是指低频情况下的电流放大系数，通常器件手册中所给的β就是β0。(www.xing528.com)

输出回路有

即

故有

由式（4.4.2）、式（4.4.3）可知，BJT高频小信号模型中也要采用静态工作点上的参数。

BJT高频小信号模型中的电容Cb′c一般在2～10 pF范围内，在近似估算时，可用器件手册中提供的Cob代替。Cob是BJT接成共基极形式且发射极开路时，集电极-基极间的结电容。而电容Cb′e可由下式计算得到

也可以由BJT的共射极截止频率fβ来计算，fβ是使|β|下降为0.707β时的信号频率，可用器件手册中提供的参数。

由于

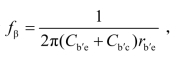电容Cb′c用Cob代替，则有

式中截止频率βf可查器件手册得到。βf越高，表明BJT的高频性能越好，由它构成的放大电路的上限频率就越高。

需要说明的是，图4.4.1（b）所示的BJT高频小信号模型只能在小于β/3f的频率范围内适用，更高的频段需用更为精确的模型。

4.4.1.3　BJT混合π模型的简化

令Cμ= Cb′c，Cп= Cb′e，可以得到图4.4.3（a）所示的BJT的高频小信号模型。Cμ跨接在输入与输出回路之间，使电路的分析变得十分复杂。因此，为简单起见，将Cμ等效到输入回路和输出回路中去，称为单向化。单向化是通过等效变换来实现的。设Cμ折合到b′-e间的电容为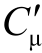，折合到c-e间的电容为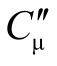，则单向化之后的电路如图4.4.3（b）所示。

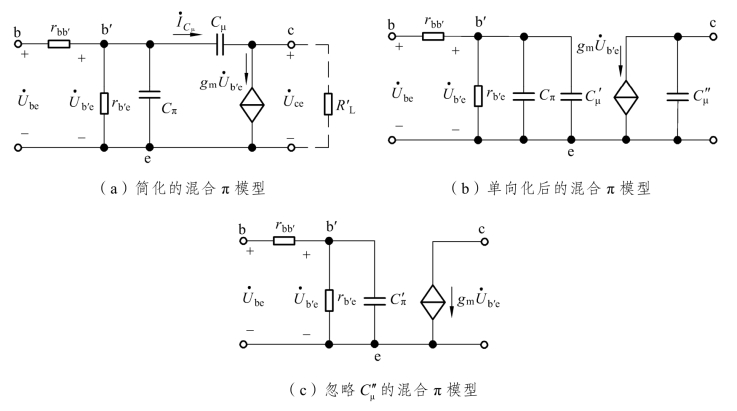
图4.4.3　混合π模型的简化

b′-e间的电容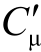为

c-e间的等效电容为

通常有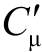＞＞Cμ，≈ Cμ，所以可以忽略，于是图4.4.3（b）可简化为图4.4.3（c）的形式，其中