共射极放大电路低频响应优化

上一节以单时间常数RC高通电路和低通电路为例，介绍了频率响应的分析方法。本节以共源和共射放大电路为例，分析耦合电容和旁路电容对放大电路低频特性的影响。

现以图4.3.1（a）所示电路为例，讨论共射放大电路的低频特性。

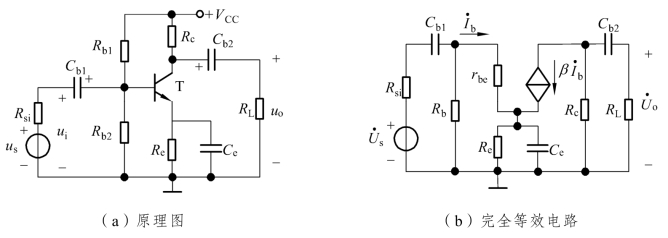
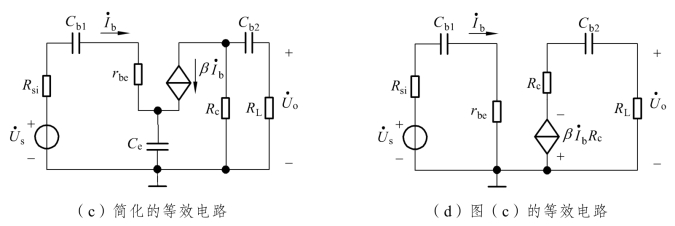
图4.3.1　共射放大电路及其低频小信号等效电路

图4.3.1（b）是图4.3.1（a）所示电路的低频小信号等效电路，其中Rb= Rb1//Rb2。为简化分析，需对此电路做一些合理的近似。首先假设Rb远大于此放大电路的输入电阻，以致Rb的影响可以忽略（将其开路）；其次假设Ce的值足够大，以至在低频范围内，它的容抗XCe远小于Re的值，即

由此可将Re视为开路，于是得到图4.3.1（c）所示的简化等效电路。然后再将电容Ce折合到基极回路，用′表示，其容抗为

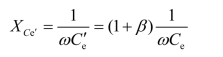
则折算后的电容为

它与耦合电容Cb1串联连接，所以基极回路的总电容为

Ce对输出回路基本上不存在折算问题，因为而且一般有Ce＞＞Cb1，因而Ce对输出回路的作用可忽略（作短路处理），这样就可得图4.3.1（d）所示的简化电路，图中还把受控电流源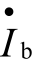β与Rc的并联回路转换成了等效的电压源形式。

图4.3.1（d）的输入回路和输出回路都与图4.2.2所示的RC高通电路相似。由图4.3.1（d）可得

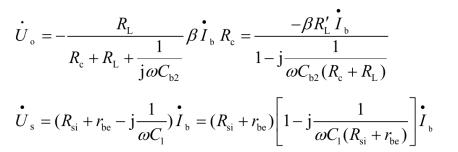
则低频源电压增益为

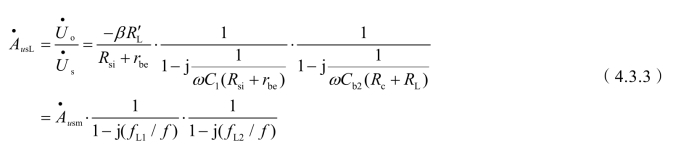
式中，

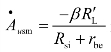是忽略基极偏置电阻Rb时的中频（即通带）源电压增益。

由此可见，图4.3.1（a）所示的RC耦合单级共射放大电路在满足式（4.3.1）的条件下，它的低频响应具有fL1和fL2两个转折频率，如果二者的比值在4倍以上，则取值大的那个作为该电路源电压增益的下限频率。

需要指出的是，由于旁路电容Ce在射极回路里，流过它的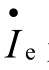电流是基极电流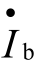的（1+β）倍，它的大小对电压增益的影响较大，因此Ce是影响低频响应的主要因素。

当Cb2很大时，可以只考虑Cb1、Ce对低频特性的影响，此时式（4.3.3）简化为

其对数幅频特性和相频特性的表达式为(www.xing528.com)

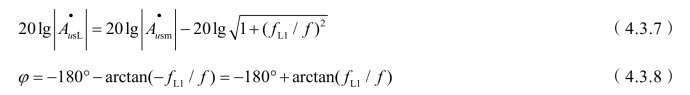
式（4.3.8）中，+arctan（fL1/f）是输入回路中等效电容C1在低频范围内引起的附加相移Δφ，其最大值为+90°；当f = fL1时，Δφ = +45°。

由式（4.3.7）和式（4.3.8）即可画出图4.3.1（a）所示电路在只考虑电容Cb1和Ce影响时的低频响应波特图。

例4.3.1　在图4.3.1（a）所示电路中，设BJT的β = 80，rbe≈ 1.5 kΩ，VCC= 15 V，Rsi= 50 Ω，

Rb1= 110 kΩ，Rb2= 33 kΩ，Rc= 4 kΩ，RL= 2.7 kΩ，Re= 1.8 kΩ，Cb1= 30 μF，Cb2= 1μF，Ce= 50 μF，试估算该电路源电压增益的下限频率。

解：由式（4.3.2）求得输入回路等效电容为

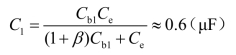
由式（4.3.4）和式（4.3.5）分别求得

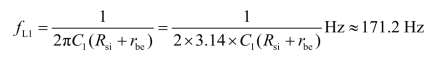
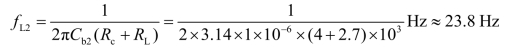
fL1与fL2的比值大于4，因此下限频率为fL≈ fL1≈ 171.2 Hz。

思考题

4.3.1　放大电路在低频信号作用时，放大倍数数值下降的原因是（　　）。

A.耦合电容和旁路电容的存在

B.半导体管极间电容和分布电容的存在

C.半导体管的非线性特性

D.放大电路的静态工作点不合适

4.3.2　对于单管共射放大电路，当f = fL时，Uo与Ui相位关系是（　　）。

A.+45°　　B.-90° 　　C.-135°

习　题

4.3.1　试求图题4.3.1所示电路的中频源电压增益musA˙和源电压增益的下限频率fL。已知VCC= 3 V，Rsi= 0.1 kΩ，Rb= 153 kΩ，Rc= 1 kΩ，RL= 5 kΩ，Cb1= 1 μF，Cb2= 1.5 μF。BJT的β = 100，UBE= 0.7 V。

4.3.2　电路如图题4.3.2所示，已知BJT的β = 50，rbe= 0.72 kΩ。试估算该电路源电压增益的下限频率。

图题4.3.1

图题4.3.2