图4.2.2所示电路为单时间常数RC高通电路。设其电压增益为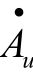 ,由图可得
,由图可得


图4.2.2 RC高通电路

则式(4.2.1)变为

将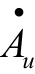 分别用幅值(模)和相角表示,得
分别用幅值(模)和相角表示,得

![]()
式(4.2.4)称为幅频响应,表明电压增益的幅值随频率的变化;式(4.2.5)称为相频响应,表明输出信号与输入信号间的相位差随频率的变化。
在研究放大电路的频率响应时,输入信号(即加在放大电路输入端的测试信号)的频率范围常常设置在几赫到上百兆赫甚至更宽;而放大电路的放大倍数可从几倍到上百万倍;为了在同一坐标系中表示如此宽的变化范围,在画频率特性曲线时常采用对数坐标,称为波特图。
波特图由对数幅频特性和对数相频特性两部分组成,它们的横轴采用对数刻度lgf,幅频特性的纵轴采用20lg|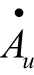 |表示,单位是分贝(dB);相频特性的纵轴仍用φ表示。这样不但开阔了视野,而且将放大倍数的乘除运算转换成加减运算。
|表示,单位是分贝(dB);相频特性的纵轴仍用φ表示。这样不但开阔了视野,而且将放大倍数的乘除运算转换成加减运算。
4.2.1.1 幅频响应
由式(4.2.4)按下列步骤可画出图4.2.1所示电路的幅频响应波特图。
(1)当f>>fL时,(fL/f)2<<1,于是有
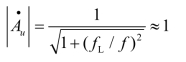
 (https://www.xing528.com)
(https://www.xing528.com)
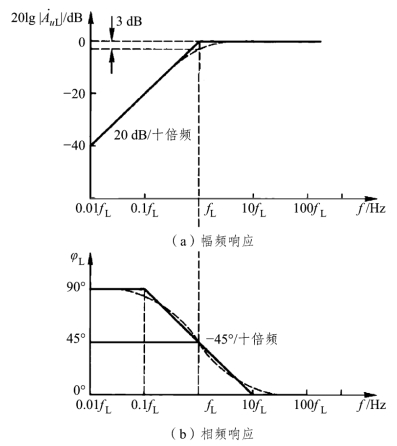
图4.2.3 RC高通电路的波特图
用分贝(dB)表示则有

这是一条与横轴平行的零分贝线。
(2)当f<<fL时,(fL/f)2>>1,于是有

用分贝(dB)表示则有

这是一条斜率为20 dB/十倍频的直线,与零分贝线在f = fL处相交。由以上两条直线构成的折线,就是近似的幅频响应曲线,如图4.2.3(a)所示。fL对应于两条直线的交点,所以fL称为转折频率。由式(4.2.4)可知,当f = fL时,
![]() 即在fL处,电压增益下降为中频值的0.707倍,用分贝表示时,下降了3 dB,所以fL又称为下限截止频率,简称为下限频率。这种用折线表示的幅频响应曲线与实际的幅频响应曲线(图4.2.3(a)中的虚线所示)存在一定误差,f = fL时误差最大,为3 dB。作为一种近似方法,这在工程上是允许的。
即在fL处,电压增益下降为中频值的0.707倍,用分贝表示时,下降了3 dB,所以fL又称为下限截止频率,简称为下限频率。这种用折线表示的幅频响应曲线与实际的幅频响应曲线(图4.2.3(a)中的虚线所示)存在一定误差,f = fL时误差最大,为3 dB。作为一种近似方法,这在工程上是允许的。
4.2.1.2 相频响应
根据式(4.2.3)可作出相频响应曲线,它可用3条直线来近似描述:
(1)当f >> fL时,φ→0°,得到一条φ = 0°的直线;
(2)当f << fL时,φ→+90°,得到一条φ = +90°的直线;
(3)当f = fL时,φ = +45°。
由于当f / fL= 0.1和f / fL= 10时,相应地可近似得φ = +90°和φ = 0°,故在0.1fL和10 fL之间,可用一条斜率为-45°/十倍频的直线来表示,于是可画得相频响应曲线如图4.2.3(b)所示。
图中亦用虚线画出了实际的相频响应曲线。同样,作为一种工程近似方法,存在一定的相位误差也是允许的。最大相位误差为5.7°,发生在f = 0.1fL和f = 10fL处。
由上述分析可知,当输入信号的频率f>fL时,RC高通电路的电压增益的幅值| |最大,而且不随信号频率变化而变化,即f>fL的高频信号能不被衰减地传输到输出端,通频带内的电压增益
|最大,而且不随信号频率变化而变化,即f>fL的高频信号能不被衰减地传输到输出端,通频带内的电压增益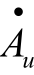 ≈ 1,也不产生明显的相移。当f = fL时,|
≈ 1,也不产生明显的相移。当f = fL时,|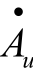 |下降3 dB,且产生+45°相移(这里的正号表示输出电压超前于输入电压)。当f<fL后,随着f的下降,|
|下降3 dB,且产生+45°相移(这里的正号表示输出电压超前于输入电压)。当f<fL后,随着f的下降,|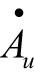 |按一定的规律衰减,且相移增大并最终趋于+90°。掌握RC高通电路的频率响应,将有助于对放大电路低频响应的分析与理解。
|按一定的规律衰减,且相移增大并最终趋于+90°。掌握RC高通电路的频率响应,将有助于对放大电路低频响应的分析与理解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




