二极管分析方法及应用

在电子技术中，利用二极管的单向导电性，可以构成许多二极管应用电路，如整流电路、限幅电路、开关电路等。由二极管的I-U特性可知，二极管是一种非线性器件，因此，一般需要采用非线性电路的分析方法来分析设计二极管电路，相对来说比较复杂。实际上经常采用两种方法来简化二极管电路的分析，一种是图解分析法，另一种是简化模型分析法。图解法无需理会线性与非线性问题，简单直观，但前提条件是已知二极管的I-U特性曲线。简化模型法是将二极管的非线性关系近似为几段线性关系，从而获得二极管的分段线性简化模型。这样，就可以用线性电路分析方法来分析二极管电路了。

二极管的伏安特性具有非线性，为了便于分析，常在一定的条件下，用线性元件所构成的电路来近似模拟二极管的特性，并用之取代电路中的二极管。能够模拟二极管特性的电路称为二极管的等效电路，也称为二极管的等效模型。通常，人们通过两种方法建立模型：一种是根据器件物理原理建立等效电路，由于其电路参数与物理机理密切相关，因而适用范围广，但模型较复杂，适于计算机辅助分析；另一种是根据器件的外特性来构造等效电路，因而模型较简单，适于近似分析。根据二极管的伏安特性可以构造多种等效电路，对于不同的应用场合，不同的分析要求，应选用其中一种。

1.2.1.1　静态模型

二极管的理想模型、恒压降模型和折线模型反映了二极管正常工作在正偏和反偏时的全部特性，这些模型常用于电路直流状态的电压或电流的估算，也称为静态模型。

1.理想模型

图1.2.5表示理想二极管的I-U特性。由图1.2.5（a）可见，在正向偏置时，是一条与纵轴重合的垂线，表明管压降为0 V；而当二极管处于反向偏置时，是一条与横轴重合的水平线，认为此时的电阻为无穷大，电流为零。图中的虚线表示实际二极管的I-U特性。图1.2.5（b）为理想二极管的代表符号（注意三角形是实心的）。图1.2.5（c）和图1.2.5（d）分别为二极管正偏和反偏时的电路模型。在实际电路中，当电源电压远比二极管的正向管压降大时，利用此模型来近似分析是可行的。

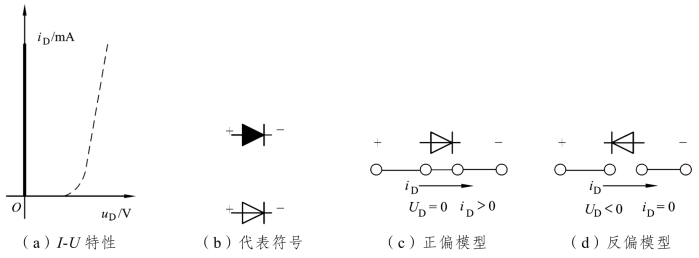
图1.2.5　理想模型

2.恒压降模型

恒压降模型如图1.2.6所示，其基本思想是当二极管导通后，认为其管压降是恒定的，且不随电流变化，在图1.2.6（a）中以垂线表示，其横轴对应的电压典型值为0.7 V（硅管）或0.2 V（锗管）。图1.2.6（b）是二极管恒压降电路模型。该模型提供了合理的近似，因此应用也较广。

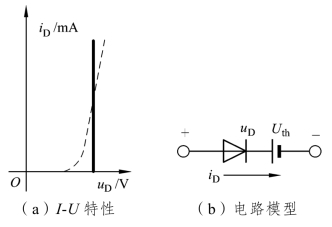
图1.2.6　恒压降模型

图1.2.7　折线模型(www.xing528.com)

3.折线模型

为了较真实地描述二极管的I-U特性，在恒压降模型的基础上做一定的修正，即认为二极管的正向管压降不是恒定的，而是随着流过二极管的电流增加而增加，所以在模型中用一个电池和一个电阻rD来做进一步的近似（参见图1.2.7）。这个电池的电压选定为二极管的开启电压Uth，约为0.5 V（硅管）。至于rD的值，可以这样来确定，即当二极管的导通电流为1 mA时，管压降为0.7 V，于是rD的值可计算如下：

1.2.2.2　动态模型

动态即电路在一定的直流工作情况下再叠加一个小的变化状态。当仅考虑小信号变化时所建立的模型称为小信号模型。

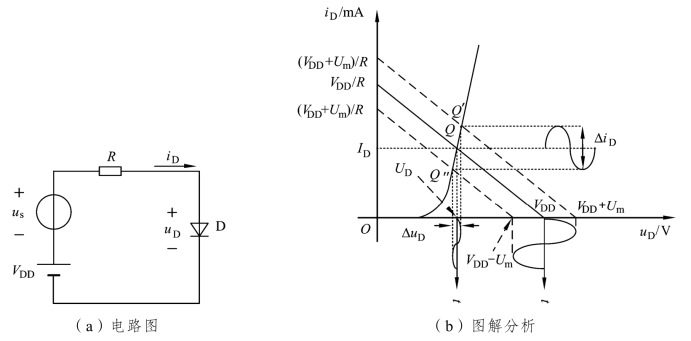
图1.2.8　直、交流电压源同时作用时的二极管电路

如图1.2.8（a）的电路中直流电源VDD中又串联了一个交流小电压信号us。当us= 0时， 电路中只有直流量，二极管两端电压和流过二极管的电流就是图1.2.8（b）中Q点的值。此时，电路处于直流工作状态，也称静态，Q点也称为静态工作点。当us=Umsin ωt时（Um＜＜VDD），电路的负载线为

根据us的正负峰值+Um和-Um图解可知，工作点将在Q′和Q"之间移动，则二极管电压和电流变化为ΔuD和ΔiD。由上看出，在交流小信号us的作用下，工作点沿I-U特性曲线，在静态工作点Q附近小范围内变化，此时可把二极管I-U特性近似为以Q点为切点的一条直线，其斜率的倒数就是小信号模型的微变电阻rd，由此得到小信号模型如图1.2.9所示。

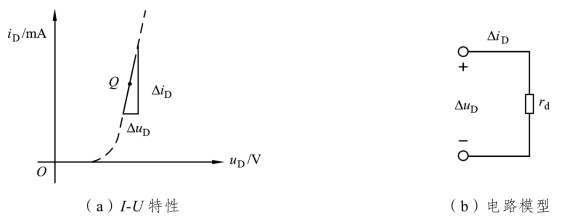
图1.2.9　小信号模型

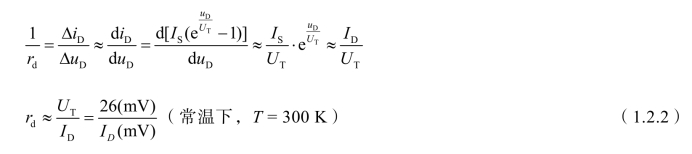
式中的ID是Q点的电流。值得注意的是，小信号模型中的微变电阻rd与静态工作点Q有关，静态工作点位置不同，rd的值也不同。由于二极管正向特性为指数曲线，所以Q点愈高，rd的数值愈小。例如，当Q点上的ID= 2 mA时，rd= 26 mV/2 mA = 13 Ω。该模型主要用于二极管处于正向偏置且UD＞＞UT的条件下。