3PTP信道多播容量方案

像前面章节介绍的，假设小区中用户均匀分布，路径损耗指数ω=4，第i个用户的平均I_oc/S₀为小区边缘最坏情况平均值的_η=0.24倍。因此可以将分配给第i个用户的平均传输功率表达为

式中 α_i——第i个用户活跃因子占空比。

因此相比于连续传输的情况（α_i=1），时间平均传输功率根据因子α_i减少。

MS接收的E_b/I₀根据数据传输速率R和分配给第i个用户的相应功率ϕ_i的比例而有所不同。语音和多播用户接收的E_b/I₀为

式中 R_v和R_m——数据传输速率；

γ_v和γ_m——要求的E_b/I₀；

ϕ_i（v）和ϕ_i（m）——分配给第i个用户的语音和多播业务的功率占BS发射功率的比例。

在重新整理式（A.4）和式（A.5）后，分配给第i个用户语音和多播业务的功率比例可以写为(www.xing528.com)

当功率控制并不理想时，假设误差是标准差为σ_e（单位为dB）的对数正态分布。如果考虑到PCE，需引入另一个乘性对数正态因子（multiplicative lognormal f_actor）。由于考虑了PCE，式（A.6）和式（A.7）中y_i（r_i，θ_i）的均值和标准差为m_t=m_y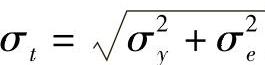，，其中m_y和σ_y分别是不考虑PCE的y_i（r_i，θ_i）的均值和标准差。因此PCE仅仅影响y_i（r_i，θ_i）的标准差，而其均值保持不变。

在下行链路上，所有公共和专用信道共享有限的BS总传输功率。因此在总的BS功率不足以满足所有用户的功率要求时发生中断。通过考虑平均下行链路功率因子η，BS中断概率为

式中 K_v和K_m——语音和多播数据用户数；

α_i^（v）和α_i^（m）——每个语音用户和多播用户的活跃因子或占空比。

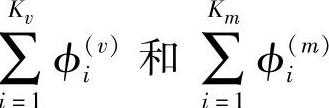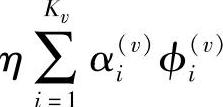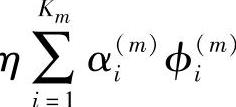由于是独立同分布的对数正态随机变量，我们分别通过对数正态随机变量Z_v和Z_m大致估计和。由于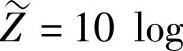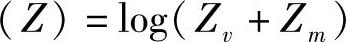是一个正态随机变量，BS中断概率可以写为

其中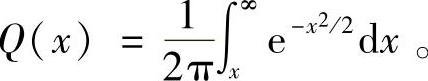

一个共同的假设是网络中每个小区表现为独立的M/M/∞队列。因此，语音和多播用户数K_v和K_m，是均值分别为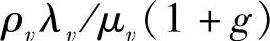和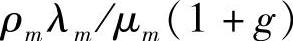的泊松随机变量。其中，λ_（·）和μ_（·）分别是语音和多播业务的到达率和离开率。在假设到网络中每个小区的数据流相同（符合随机模型的参数，但不同于假设每个小区都有等量的静态负载）的情况下，g是来自相邻小区处于软切换的用户比例。处于软切换中的用户相比于没有处于软切换的用户，带来大约2倍的干扰。我们假设占所有用户中比例g＜1的用户处于双向软切换，且参与软切换的两个BS分配相同比例的功率给软切换用户。每个BS的有效到达率从λ增加到λ（1+g）。保持BS中断概率在目标水平（通常0.01）的Erlang容量A_v=λ_v/μ_v和A_m=λ_m/μ_m。