平均下行链路功率因子的推导方法

Lee和Miller首先推导了单小区系统的平均下行链路功率因子η，随后Choi和Kim推导了多小区系统的情况。我们的推导与Choi和Kim不同，因为我们考虑了整个小区边缘I_oc的变化，更适合多小区系统。

令z（r，θ）表示小区中指定位置（r，θ）的I_oc/S₀。我们要确定小区中I_oc/S₀的变化关于位置的函数，忽略阴影衰落，仅仅将I_oc/S₀表达为距离相关传播损耗的函数。本地小区中MS（x，y）到第j个BS（R_j，θ_j）的距离定义为。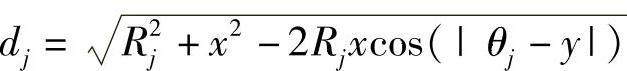

整个小区内I_oc/S₀的平均值计算为

式中 ω——路径损耗指数；

f_r，θ（x，y）——本部分中所有MS的概率密度函数（pdf）；

θ_s——扇区方向角。(www.xing528.com)

pdff_r，θ（x，y）为

由于我们考虑的是一个全向小区，θ_s=2π，pdf改写为

现在我们来计算整个小区边界圆周上I_oc/S₀的平均值，换句话说，到BS距离为R_c时

其中

其中pdf表现的是最坏情况的场景，并描绘了沿着本地小区边界的MS分布。在（Choi and Kim，2001a）中，η的推导仅考虑了小区边缘最坏情况的点。这在一个多小区系统中是不合适的，因为I_oc会沿着本地小区的边界变化。平均下行链路功率因子η可以被表达为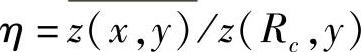，其中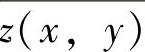和z（R_c，y）分别在式（A.2）和式（A.3）中给出。路径损耗指数ω=4时，平均下行链路功率因子计算为η=0.24。