如何降低小区间干扰比率与接收功率

对所有可能的（r_i，θ_i）值计算z_i（r_i，θ_i）是困难的。由于图A.1中展示的3层小区规划的对称性，I_oc/S₀的最坏情况在参考小区的6个角上，在这些地方I_oc/S₀的值是相等的。为了为干扰建立容易解析的参考情况我们计算距离本地基站的距离为d，θ=0（也就是在图A.1上沿x轴叠加）时的I_oc/S₀，且令这为干扰的最坏情况。这样做是合理的，首先因为S₀=P₀·L₀独立于θ，因此仅是关于d的函数。其次因为在任意距离d，θ=0时评估I_oc考虑到了来自相邻小区的主要干扰源。因此到BS距离为d，θ=0的I_oc/S₀是位于（d，θ）的MS的最坏情况干扰功率。

距离本地基站为d的地方接收到本地基站的功率为S₀=P₀·L₀=d^-ω·χ₀。像（Choi and Kim，2001a）中一样，我们仅考虑从11个最近的BS来的小区间干扰，因为从其他BS来的干扰相比于这11个最近BS的可以被忽略。根据图A.1中给出的小区编号，假设所有BS全功率发射，小区间干扰功率占从本地基站接收到的功率的比例是到本地基站的距离d的函数，θ=0，记z（d）=I_oc/S₀

令m_i和σ_i分别表示I_oc的均值和标准差（单位为dB），m_s和σ_s分别表示S₀的均值和标准差。I_oc和S₀的均值和标准差可以分别从式（A.1）的分子和分母计算。I_oc/S₀的均值m_z和标准差σ_z（单位为dB）可以分别计算为m_z=m_i-m_s，。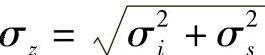

我们使用胡氏算法（Ho and Akyildiz，1996）评估对数正态分布随机变量的总和，如式（A.1）的分子。在计算均值和标准差方面胡氏算法比其他的通用算法更加准确。(www.xing528.com)

随着MS从小区中心移动，来自本地基站的总接收功率S₀下降，而小区间干扰I_oc增加。因此，I_oc/S₀的均值m_z和标准差σ_z随着MS向小区边界外移动而增加。在σ=4.5dB的阴影蔓延情况下，使用胡氏算法计算小区间干扰，到本地基站距离为d的I_oc/S₀的均值和标准差（以dB为单位）在表A.1中列出。

图A.1 下行链路小区间干扰模型

表A.1 I_oc/S₀的均值和标准差