解析三相电路的功率特点与计算方法

1.平均功率（有功功率）

负载工作是要消耗电能的，其所消耗的能量可以用平均功率来表示。将一个周期内瞬时功率的平均值称为平均功率，也称有功功率。有功功率为

可见对交流电路而言，其平均功率等于负载上的电压与电流有效值和cosφ的乘积。无论电路的连接形式如何，φ角均为电路负载的阻抗角，也就是电路中电压与电流的相位差。当负载一定时，cosφ是一常数，称为负载的功率因数，φ角则称为功率因数角。

（1）当电路为纯电阻电路时，电压与电流同相，即

φ=0，cosφ=1，P=UIcosφ=UI

（2）当电路为纯电感或纯电容电路时，电流与电压的相位差均为90°，cosφ=0，所以P=UIcosφ=0，与前面的讨论完全一致。注意：本项目中的U、I为有效值。

2.无功功率

电路中的电感元件与电容元件要与电源之间进行能量交换，根据电感元件、电容元件的无功功率，考虑到相位相反，则

在感性电路中，由于sinφ为正值，所以Q为正值，即QL＞QC；在容性电路中，sinφ为负值，所以Q为负值，即QL＜QC。显然，在既有电感又有电容的电路中，总的无功功率为QL与QC的代数和，即

3.视在功率

在实际交流电路中，电器设备所消耗的有功功率是由电压、电流和功率因数决定的。但在制造变压器等电器设备时，用电设备（即负载）的功率因数是不知道的。因此这些设备的额定功率不能用有功功率来表示，而是用额定电压与额定电流的乘积来表示，我们把它称为视在功率，即

视在功率常用来表示电器设备的容量，其单位为VA（伏安）。视在功率不是表示交流电路实际消耗的功率，而只能表示电源可能提供的最大功率，或指某设备的容量。

4.功率三角形

将交流电路表示电压间关系的电压三角形的各边乘以电流I即成为功率三角形，如图6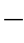31所示。

图631　功率三角形

由功率三角形可得到P、Q、S三者之间的关系如下

5.功率因数

前面提过功率因数cosφ，其大小等于有功功率与视在功率的比值，在电工技术中，一般用λ表示，当负载为纯电阻负载时，cosφ=1；但对大部分负载而言，功率因数一般在0～1之间，如计算机的功率因数一般为0.6左右，异步电动机在额定情况下工作时为0.6～0.9，工频感应加热炉为0.1～0.3，日光灯为0.5～0.6。

φ角称为功率因数角，它既是电路总阻抗的阻抗角，又是该电路端电压与总电流的相位差角。

【例631】已知电阻R=30Ω，感抗XL=120Ω，容抗XC=80Ω，串联后接到电压u=220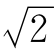sin（314t+30°）V的电源上。求电路的P、Q和S。

解：电路总阻抗的大小为

阻抗的方向为(www.xing528.com)

根据u=220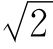sin（314t+30°）V，可知电压有效值为U=220V，则电流的有效值为

电路的平均功率　P=UIcosφ=220×4.4×cos53°=58（W）

电路的无功功率　Q=UIsinφ=220×4.4×sin53°=774（var）

电路的视在功率　S=UI=220×4.4=968（VA）

由以上可见，φ＞0，电压超前电流，因此电路为感性。

6.三相电路的功率

我们知道，计算单相电路中的有功功率的公式是P=UIcosφ，式中，U、I分别表示单相电压和单相电流的有效值，φ是电压和电流之间的相位差。在三相交流电路中，三相负载消耗的总电功率为各相负载消耗功率之和，即

当三相电路对称时，由于每一相的电压和电流都相等，阻抗角φ也相同，所以各相电路的功率必定相等，可以把它看成是三个单相交流电路的组合，因此三相交流电路的功率等于三倍的单相功率，即

在一般情况下，相电压和相电流不容易测量。例如，三相电动机绕组接成三角形时，要测量它的相电流就必须把绕组端部拆开。因此，通常用线电压和线电流来计算功率。

当三相对称负载星形连接时，则有UL=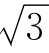UP，IL=IP。

如果三相对称负载三角形连接，则有UL=UP，IL=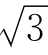IP。

因此，对称负载不论是作星形连接还是作△形连接，其总有功功率均为

必须注意，φ仍是相电压与相电流之间的相位差，而不是线电压与线电流间的相位差。同样的道理，对称三相负载的无功功率和视在功率也一样，即

如果三相负载不对称，则应分别计算各相功率，三相的总功率等于三个单相功率之和。

【例632】有一对称三相负载，每相电阻为R=6Ω，电抗X=8Ω，三相电源的线电压为UL=380V。式求：

（1）负载做星形连接时的功率P。

（2）负载做三角形连接时的功率P△。

解：每相阻抗均为，功率因数λ=cosφ==0.6。

（1）负载做星形连接时：

（2）负载做三角形连接时：