优化办公网络的拓扑结构

在将计算机连入网络时，要使用通信线路。而通信线路又有不同的分布方式。计算机网络设备与通信线路结合起来的总体布局模型称为网络的拓扑结构。

最基本的计算机网络拓扑结构主要有星形结构、总线型结构和环形结构3种。

1.星形拓扑结构

在星形拓扑结构中，以一台设备作为中央节点（节点即计算机或网络设备与通信线路的连接端点）。然后通过点到点的方式将其他的从节点与中央节点进行连接。

图解演示

图11-7所示为星形拓扑结构的示意图。从图中可以看到中央节点可以直接与任何一个节点进行通话，而各从节点之间只能通过中央节点才能通信。因此要求中央节点要有中继和数据处理的功能，在实际中通常由集线器或交换机来承担中央节点的工作。

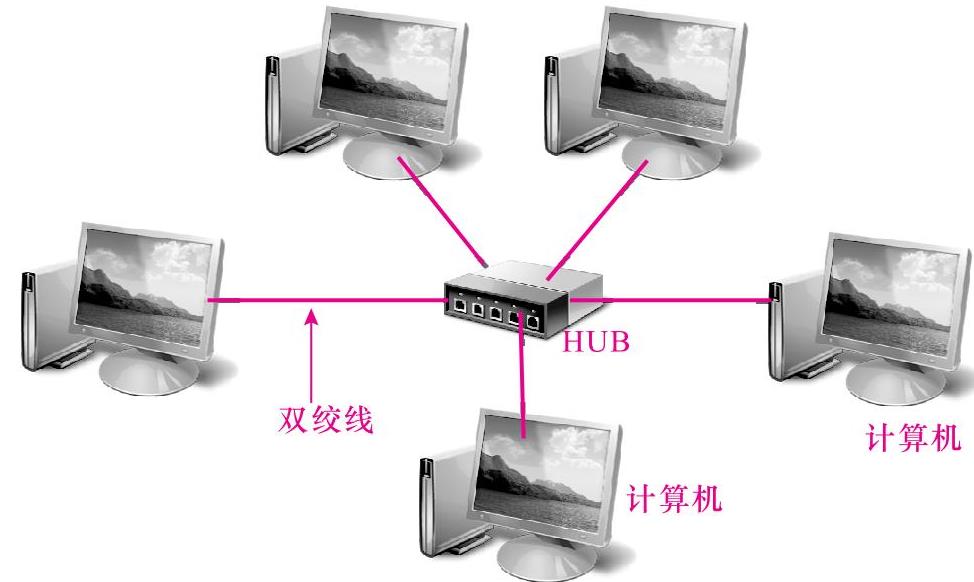
图11-7 星形拓扑结构

（1）采用星形拓扑结构的优点

●由于每个从节点都是直接与中央节点连接的，因此当需要在网络中添加或删除节点时，只需添加新的连接到中央节点上，或将需要去除的节点连接去掉即可，网络的扩充或调整十分方便。

●由于中央结点位于网络的中央，因此如果其他从节点或通信线路出现故障，则可以利用附加在中央节点中的网络诊断设备，比较准确地诊断和定位网络故障。

●由于各从节点之间不直接连接，因此网络中的任何一个从节点出现故障都不会影响到其他的节点，从而仍能保证网络的正常运转。

（2）星形拓扑结构的缺点

正是由于所有的从节点都需要与中央节点连接，因此中央节点就成了星形网络的关键性设备，一旦中央节点的设备出现故障，整个网络就会瘫痪。

由于每个从节点都需要一条单独的线路与中央节点连接，因此每增加一个节点就意味着要增加一条线路，当节点较多时，网络线路也会变得复杂，而且成本也会较高。

2.总线型拓扑结构

图解演示

图11-8所示为总线型拓扑结构的示意图。从图中我们可以看到，网络中所有节点都通过网卡直接连接到一条主干线缆（BUS）上。在主干线缆的两端分别装有终端电阻（终端电阻是用来吸收电信号的）。在网络传输时，某一节点发出一个电信号，该信号会从该点出发分别同时沿主干线缆向两端传送，主干线路上的每个节点都可以检测到该信号。同时，在主干线缆的两端处分别装有终端匹配器（或终端电阻）。当信号抵达主干线缆的尽头时，终端匹配器便会将信号吸收，使得信号不再返回传输，从而消除对其他后续信号的干扰。

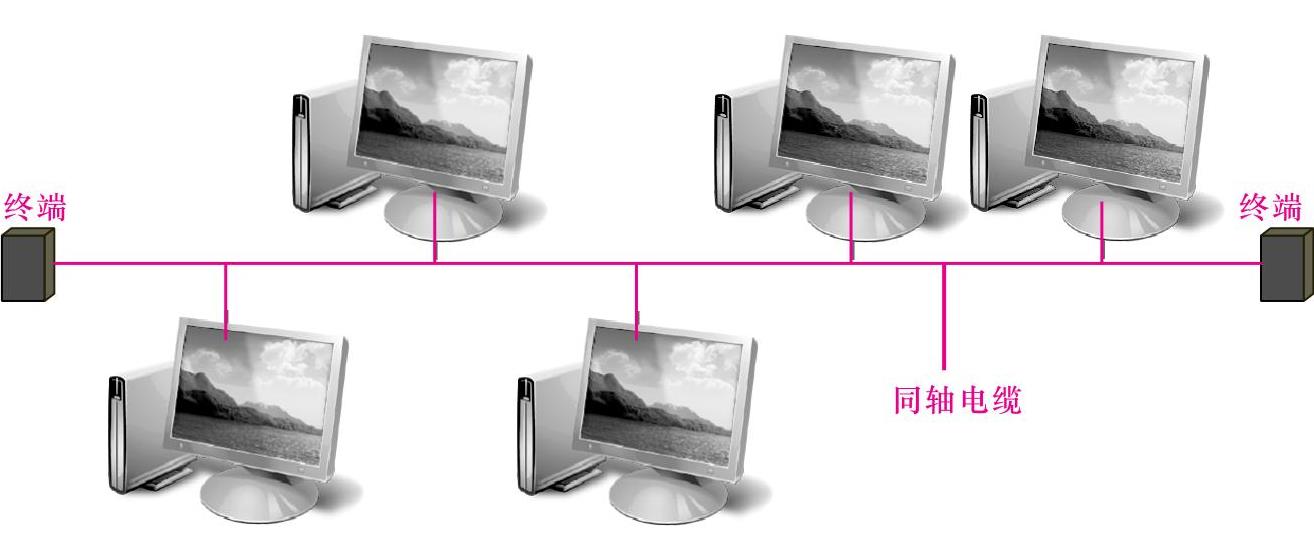
图11-8 总线型拓扑结构

（1）总线型拓扑结构的优点

●总线型网络的结构简单且使用无源组建，因此硬件系统的可靠性高、运行可靠。

●由于所有的节点都连接在一条主干线缆上，因此网络的布线安装十分简便。

●当需要添加节点时，可以在总线的任何一点接入，使得网络扩充十分方便。

●由于不需要专门的集线设备且主干线缆固定，每个节点都可以连接到总线上，因此网络的成本费用较低。

（2）总线拓扑结构的缺点

●由于网络中缺乏集中控制机制，因此当出现故障时很难准确确定故障点。(www.xing528.com)

●总线型的连接传输使得每个部件上出现故障，都有可能导致整个网络的瘫痪。

●所有节点都通过一条总线来传输信息，当传输的信息量过大时就会造成网络阻塞，影响传输速度。

3.环形拓扑结构

图解演示

在环形拓扑结构中，所有的节点都连接到一个封闭的环路上。图11-9所示为环形拓扑结构示意图。

环形拓扑结构中，每个节点都通过一个中继器连接在环路上，信息沿某一个方向在闭合的环路中逐个节点地进行传递。信息的发送是通过“令牌”（token）传递方式来控制的，在整个网络中只有一个令牌，令牌沿闭合环路传递。只有当节点获得令牌后才能发送数据，而没有获得令牌的节点只能等待。

（1）环形拓扑结构的优点

●由于环路中，由令牌控制传输，因此环形网络的数据传输率高，信息包长度也不受限制。

●由于令牌在环网中逐点传递，因此网络的传输延时确定。

●由于计算机通过中继器连接到环网，因此网络的传输距离较远。

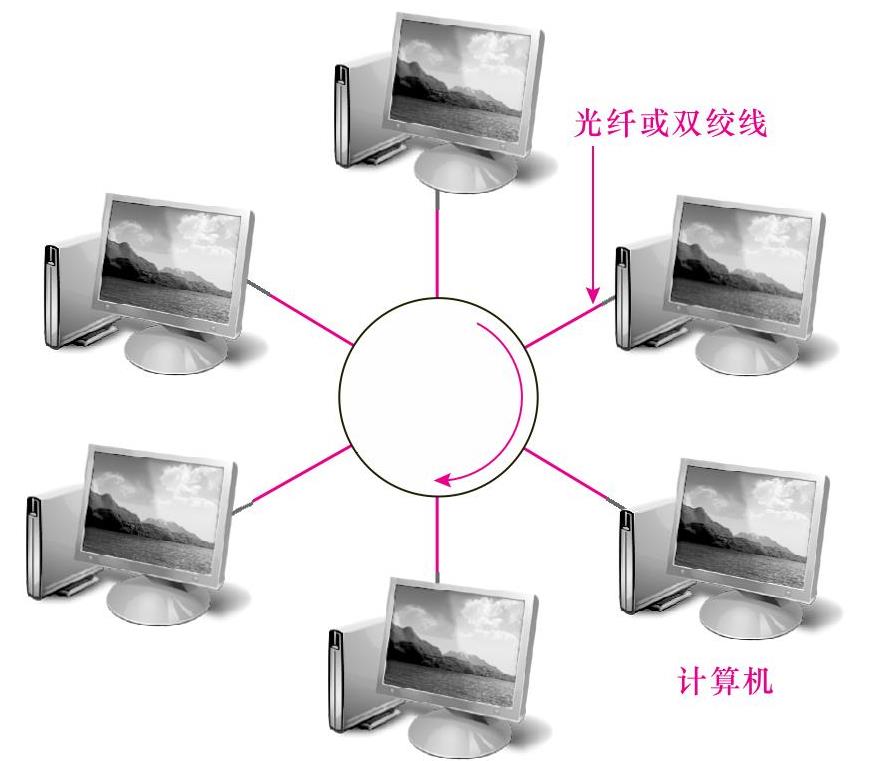
图11-9 环形拓扑结构

（2）环形拓扑结构的缺点

●由于环形网络采用逐点传输，即一个节点的信息沿一个方向先传输到下一个节点，然后再逐个节点完成传输，因此在环网中一旦有节点失效，整个网络就会瘫痪。

●由于每个节点都需要中继器才能接入网络，因此网络的成本大大增加。

●由于网络是闭合环路形式，当需要添加、删除节点时都需要对整个环路进行修改，因此网络的调整和管理都比较复杂。

相关资料

星形拓扑结构、总线型拓扑结构和环形拓扑结构是局域网的3个基本拓扑结构，当网络中的计算机增多，且需要不同功能要求时，往往就不能单纯地采用某一种基本拓扑结构，而是根据所需要的具体功能的特点，在3种基本拓扑机构的基础上进行扩展形成混合的拓扑结构。

图11-10所示为从星形拓扑结构演变出来的树形拓扑结构。图11-11所示为将星形拓扑结构融合到总线型拓扑结构中形成的星形-总线型拓扑结构示意图。图11-12所示为将星形结构融合到环形拓扑结构中形成的星形-环形拓扑结构。

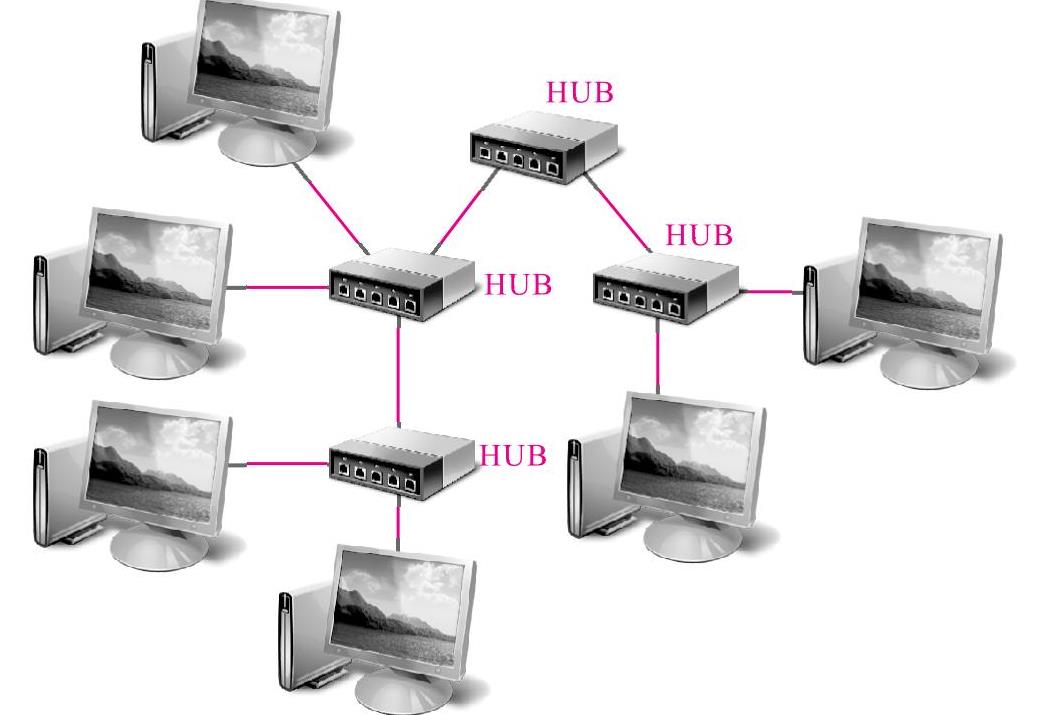
图11-10 树形拓扑结构

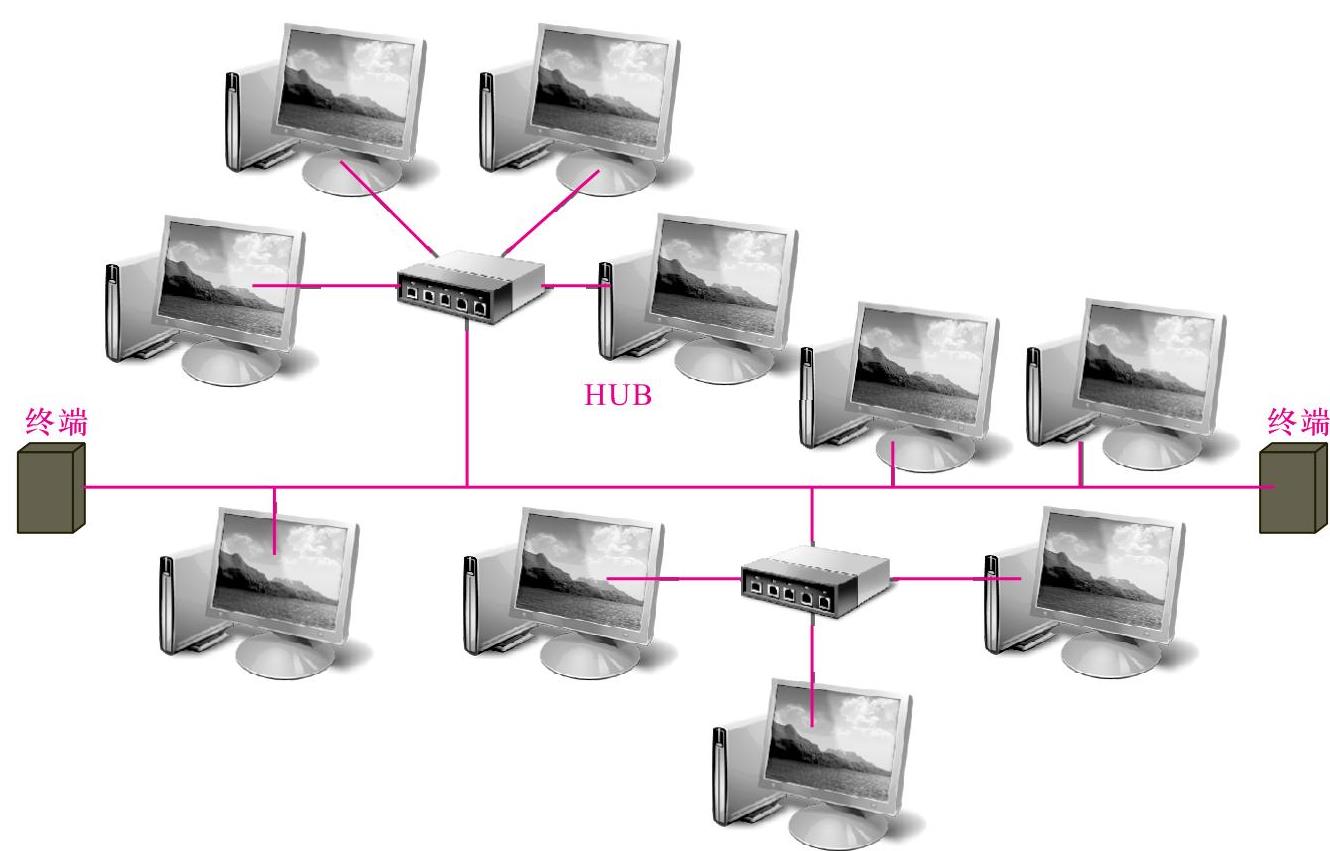
图11-11 星形-总线型拓扑结构

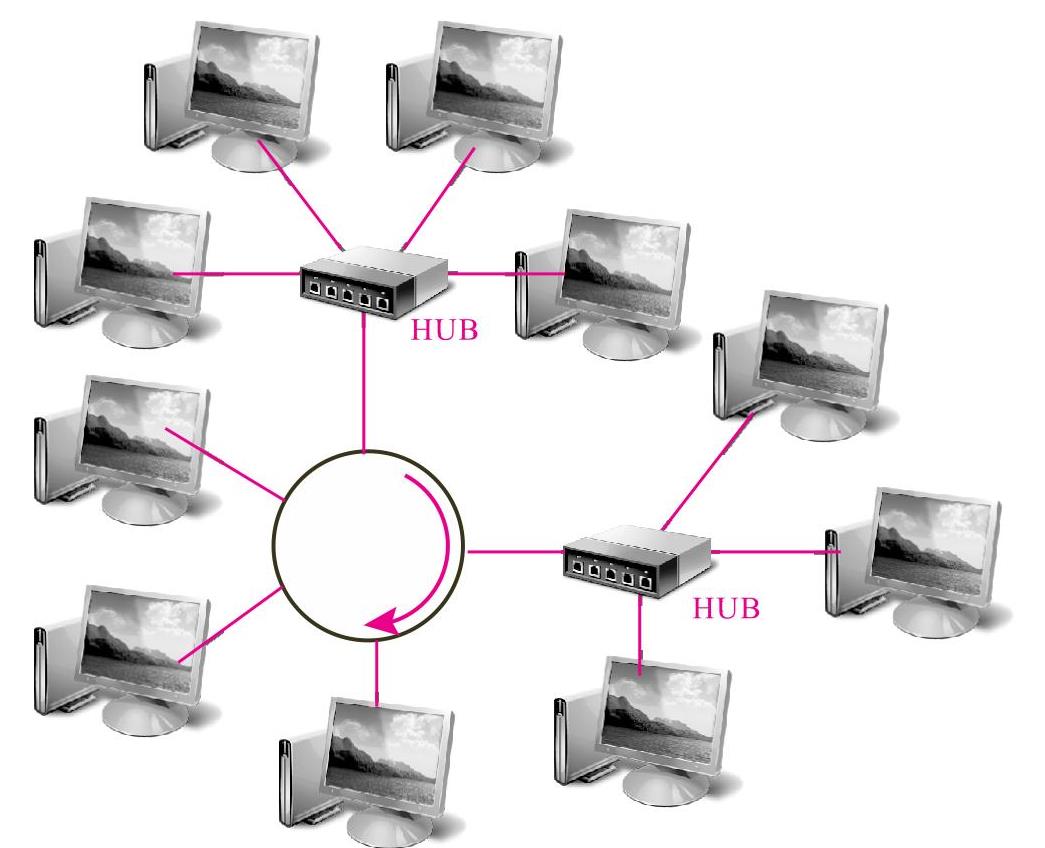
图11-12 星形-环形拓扑结构