【例3-1】 如图3-7所示,已知:系统等效电抗XM=10Ω,XN.min=30Ω、最大阻抗为无穷大;线路的正序阻抗Z1=0.45Ω/km,阻抗角φk=65°;线路上采用三段式距离保护,阻抗元件均采用方向阻抗继电器,继电器最大灵敏角φsen=65°;保护2的Ⅲ段时限为2s;线路MN、NP的最大负荷电流IL.max=400A,负荷自起动系数为2,负荷的功率因数cosφ=0.9;变压器采用差动保护,变压器容量为2×15MVA、电压比为110/6.6kV、电压阻抗百分数Uk%=10.5%。试求保护M各段动作阻抗、灵敏度及时限。
分析:阶段式距离保护Ⅰ段的动作时间为瞬时动作,可靠系数的取值即为保护区长度,因此,不必计算保护区。线路末端有助增电源时应计及分支系数,本例中远后备保护的变压器最小电抗应取并列运行情况,且电压应采用主抽头电压。

图3-7 例3-1系统接线图
【解】 (1)保护M侧的Ⅰ段动作阻抗:
Zop.M=0.85×0.45×30Ω=11.48Ω
(2)保护M侧的Ⅱ段动作阻抗。
1)与保护2第Ⅰ段配合时:
Zop.N=0.85×0.45×38Ω=14.54Ω
分支系数Kb最小值的情况是XB.max=∞时,即N电源断开,Kb=1。
Zop.M=Krel(Z1LMN+KbZop.N)=0.85×(0.45×30+14.54)Ω=23.83Ω
2)与变电所N降压变压器的速动保护配合时:
Zop·M=Krel(Z1LMN+KbZT.min)
单台变压器电抗为 ZT=(10×10.5×1102/15×103)Ω=84.7Ω
并列运行时电抗为
所以 Zop.M=0.7×(0.45×30+42.35)Ω=39.09Ω
取二者较小值为动作阻抗,即Zop.A=23.83Ω
灵敏度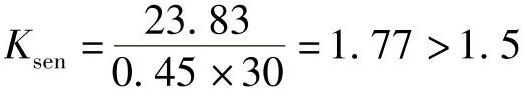 ,满足要求。
,满足要求。
保护动作时间tⅡop=Δt。
(3)保护M侧的Ⅲ段动作阻抗:
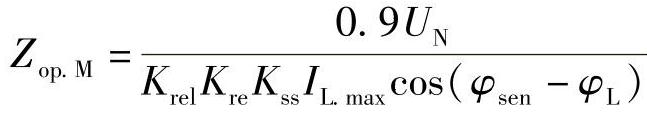 (取电压为0.9U。是考虑电压产生波动时,输送功率不变。)
(取电压为0.9U。是考虑电压产生波动时,输送功率不变。)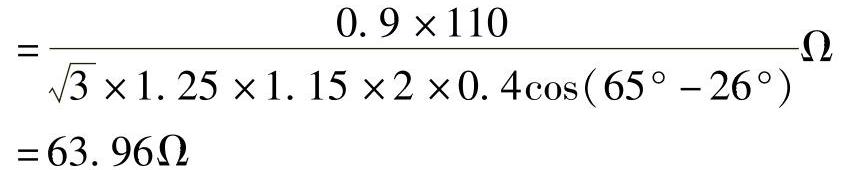
其中,φL=cos-10.9=26°
灵敏度:
①近后备时,
②远后备时,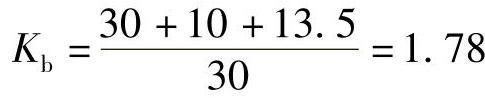 (注:远后备保护可不考虑相邻变压器。)
(注:远后备保护可不考虑相邻变压器。)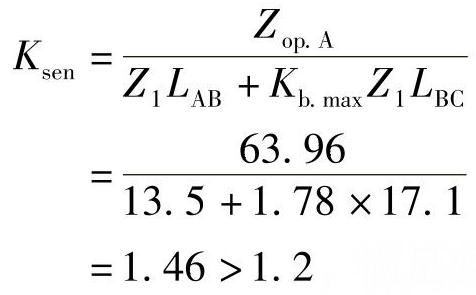 ,满足要求。
,满足要求。
动作时限:t=2s+0.5s=2.5s
【例3-2】 如图3-8所示,已知:线路正序阻抗Z1=0.45Ω/km,平行线路长70km,线路MN长40km,距离Ⅰ段保护可靠系数取0.85。M侧电源最大、最小等效阻抗分别为ZsM.max=25Ω、ZsM.min=20Ω;N侧电源最大、最小等效阻抗分别为ZsN.max=25Ω、ZsN.min=15Ω,试求线路MN的M侧距离保护的最大、最小分支系数。
分析:线路MN的M侧距离保护有助增电源,相邻线路为平行线路,即也存在汲出问题,整定计算时应同时加以考虑。汲出系数最大值为1(平行线路断开一回线路时)。
【解】 (1)最大分支系数。
1)最大助增系数:

图3-8 例3-2系统接线图

2)最大汲出系数:
显然,当平行线路只有一回路运行时,汲出系数为1。
总的最大分支系数为KbΣ=Kb助Kb汲=3.87×1=3.87。
(2)最小分支系数。
1)最小助增系数:
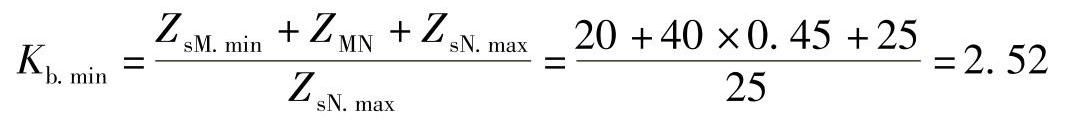
2)最小汲出系数:
由最小汲出系数公式可知,平行线路的阻抗可化为长度进行计算,则可得
 (平行线路速断保护区可根据可靠系数决定。)
(平行线路速断保护区可根据可靠系数决定。)
总的最小分支系数为KbΣ=Kb助Kb汲=2.52×0.575=1.45(在既有助增,也有汲出时,可分别求出各自的分支系数,它们的乘积为总分支系数。)
【例3-3】 在图3-9所示双电源系统中,ZL=50∠75°Ω,ZM=30∠75°Ω;ZN=20∠75°Ω,母线M侧距离保护接线方式为线电压两相电流差的方向阻抗继电器,保护采用圆特性方向阻抗继电器,M侧距离保护Ⅰ段的整定阻抗Zset=40Ω,最大灵敏角φsen=75°,EM=EN。问:
(1)当系统发生振荡时,若两侧电动势相位差δ=157.4°时,阻抗继电器会不会误动作?
(2)当系统发生振荡时,若两侧电动势相位差δ=136.4°时,继电器会不会误动作?
(3)若系统振荡周期为1.5s,继电器误动作的时间是多少?
分析:系统发生振荡时距离保护是否会误动,决定于阻抗特性元件动作区、两侧电动势夹角振荡周期。(注意:对于圆特性方向阻抗元件,当短路阻抗角与最大灵敏角不相等时,动作阻抗与整定阻抗不相等。)
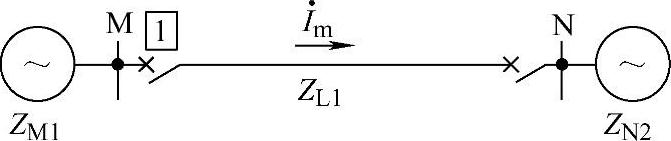
图3-9 例3-3系统接线图
【解】 (1)当δ=157.4°时,振荡电流为
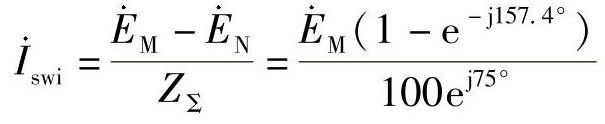
M侧母线电压为
M侧测量阻抗为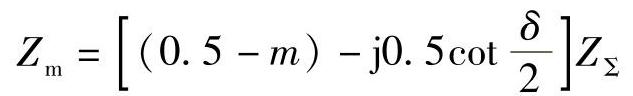
其中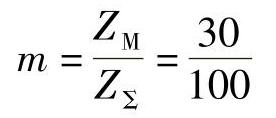
则
角度为48.4°时阻抗继电器动作阻抗为
Zop=40cos(75°-48.4°)Ω=35.7Ω>22.36Ω
方向阻抗继电器会误动作。
(2)当δ=136.4°时,测量阻抗为
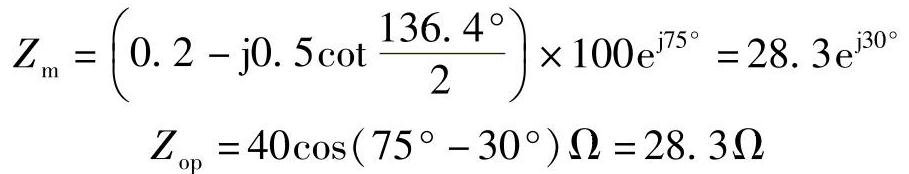
方向阻抗继电器处于临界动作状态。
(3)继电器误动时间。
Δδ=(180°-136.4°)×2=87.2°(距离保护临界动作状态即为圆特性边界,误动区中点在180°处,乘2即为误动区间。)

【例3-4】 如图3-10所示,已知:网络的正序阻抗Z1=0.4Ω/km,线路阻抗角φL=65°,变电站M、N装有反应相间短路的二段式距离保护,它的Ⅰ、Ⅱ段测量元件均采用圆特性方向阻抗继电器。试求变电站M距离保护动作值(Ⅰ、Ⅱ段可靠系数取0.8)。并分析:
(1)当在线路MN距M侧55km和65km处发生相间金属性短路时,变电站M各段保护的动作情况。
(2)当在距变电站M30km处发生过渡电阻R=12Ω的相间弧光短路时,变电站M各段保护动作情况。
(3)若变电站M的电压为115kV,通过变电站的负荷功率因数为0.9,问送多少负荷电流时,变电站M距离保护Ⅱ段才会误动作?
分析:在被保护线路不同点发生短路,阶段式距离保护是否动作,与保护安装处测量阻抗、动作阻抗有关;应注意经过渡电阻测量阻抗与过渡电阻之间的关系。
【解】 (1)线路MN距离保护M侧的Ⅰ段整定值为
Zop.M=0.8×0.4×75Ω=24Ω(取整定阻抗角为φset=65°)
线路MN距离保护M侧的Ⅱ段整定值:
其中相邻线路Ⅰ、Ⅱ段整定值为ZⅠop.N=0.8×0.4×50Ω=16Ω
ZⅡop.M=0.8×(0.4×75+16)Ω=36.8Ω
1)在55km处短路测量阻抗为 Zm=0.4×55Ω=22Ω
2)在65km处短7路测量阻抗为 Zm=0.4×65Ω=26Ω

图3-10 例3-4系统接线图
线路MN距离保护M侧的Ⅰ段不动作,Ⅱ段会动作。
(2)在距变电站M30km处经过渡电阻R=12Ω的相间弧光短路的测量阻抗为
U(2)m=2I(2)kZ1L+I(2)kR
I(2)m=2I(2)k
Zm=Z1L+0.5R(相间短路,过渡电阻值每相取一半。)=30×0.4ej65°+0.5×12=15.55ej44.6°
ZⅠop=24cos(65°-44.6°)=22.5>15.55
ZⅡop=36.8cos(65°-44.6°)=34.5>15.55
故线路MN距离保护M侧的Ⅰ、Ⅱ段均会动作。
(3)求使Ⅱ段误动的负荷电流:
φL=cos-10.9=25.8°
由整定阻抗角求出的负荷阻抗为36.8cos(65°-25.8°)=28.5时,方向阻抗继电器就会误动。
误动作时的负荷电流为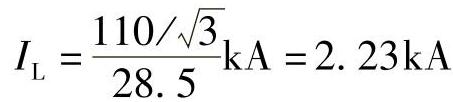
【例3-5】 已知阻抗元件由三部分组成:电抗元件、方向元件和电阻元件。其中电抗元件的动作方程为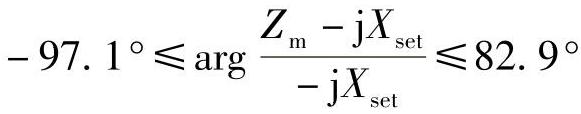 ;方向元件的动作方程为-14°≤argZm≤104°;电阻元件的动作方程为-
;方向元件的动作方程为-14°≤argZm≤104°;电阻元件的动作方程为- 。当测量阻抗同时满足上述三元件对应的动作方程时,该阻抗元件动作,否则不动作。在复平面上画出该阻抗元件的动作特性并指出动作区。
。当测量阻抗同时满足上述三元件对应的动作方程时,该阻抗元件动作,否则不动作。在复平面上画出该阻抗元件的动作特性并指出动作区。
【解】 该阻抗元件的动作特性曲线如图3-11所示。测量阻抗落在X元件、D元件、R元件所包围的区域时,测量元件动作。
【例3-6】 在图3-12所示的双端电源系统中,母线M侧装有圆特性方向阻抗继电器,其Ⅰ段整定阻抗为ZⅠset,且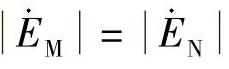 ,其参数如图所示。求:
,其参数如图所示。求:
(1)振荡中心位置,并在复平面上画出振荡时测量阻抗末端的变化轨迹;
(2)圆特性方向阻抗继电器误动作的角度范围;
(3)当系统振荡周期T=1.5s时,圆特性方向阻抗继电器误动作的时间。
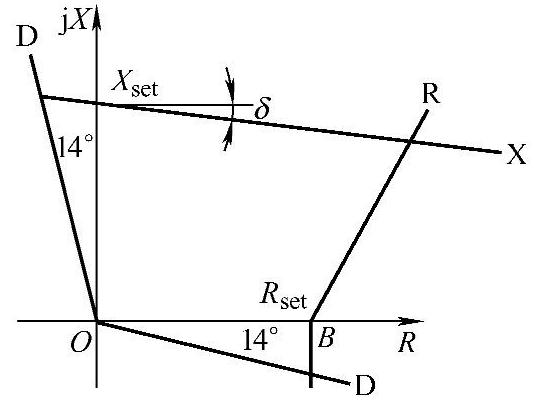
图3-11 阻抗特性图
【解】 当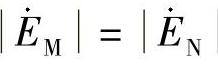 且两侧系统的阻抗角和线路阻抗角相等时,系统振荡时测量阻抗的变化轨迹为一条直线。
且两侧系统的阻抗角和线路阻抗角相等时,系统振荡时测量阻抗的变化轨迹为一条直线。
系统振荡时,安装在M侧的测量元件的测量阻抗为
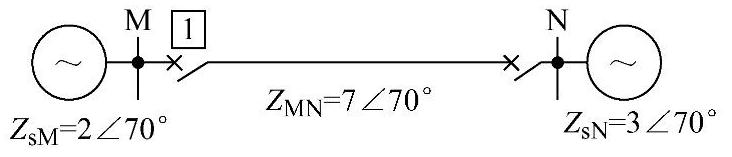
图3-12 例3-6系统接线图
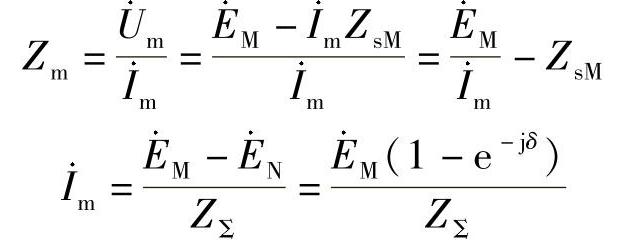
由以上两式求解得

其中, 。振荡中心在点O,线段AO所对应的阻抗为4∠70°。直线1为测量阻抗末端的变化轨迹。测量阻抗末端在CD之间移动时,安装在M侧的方向阻抗继电器会误动作。由几何知识可得OD/4=2/OD,得
。振荡中心在点O,线段AO所对应的阻抗为4∠70°。直线1为测量阻抗末端的变化轨迹。测量阻抗末端在CD之间移动时,安装在M侧的方向阻抗继电器会误动作。由几何知识可得OD/4=2/OD,得 。图3-13中线段OD和DM之间夹角为
。图3-13中线段OD和DM之间夹角为
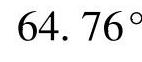 。所以误动的角度范围为129.52°~230.48°。
。所以误动的角度范围为129.52°~230.48°。
方向元件误动时间为
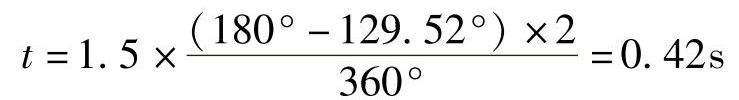
【例3-7】 如图3-14所示网络,在保护1~4处安装有三段式距离保护,其测量元件采用方向阻抗继电器。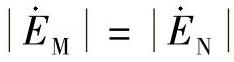 ,且全系统阻抗角均为60°,线路电抗X=0.4Ω/km,线路长度L1和L2按3种方案列于表3-1中。
,且全系统阻抗角均为60°,线路电抗X=0.4Ω/km,线路长度L1和L2按3种方案列于表3-1中。

图3-13 测量阻抗变化轨迹
(1)分析各种方案中保护1、保护4的Ⅰ段和Ⅱ段以及保护2、保护3的Ⅰ段中哪些保护受系统振荡的影响?(可靠系数取0.8)。
表3-1 3种方案参数

(2)试比较图3-15所示全阻抗、方向阻抗、橄榄型阻抗继电器动作特性,在整定阻抗相同的情况下,躲系统振荡能力有何不同?(系统各元件阻抗角相等)
【解】 电力系统振荡时,阻抗元件是否会误动作、误动作的时间长短与保护安装位置、保护动作范围、动作特性的形状和振荡周期有关。安装位置离振荡中心越近、整定值越大、动作特性与整定阻抗垂直方向的动作区越大,越容易受振荡的影响,振荡周期越长,误动的时间越长。

图3-14 例3-7系统接线图
(1)方案1:振荡中心在母线N上。曲线OO′为保护1测量阻抗末端的移动轨迹,如图3-16所示。从图中可看出,保护1和保护4的Ⅰ段不受振荡的影响,保护1和保护4的Ⅱ段、保护2和保护3的Ⅰ段都受振荡的影响。
方案2:振荡中心在线路MN上距母线N25km处。保护1的Ⅰ段和Ⅱ段、保护2的Ⅰ段、保护4的Ⅱ段受系统振荡影响。
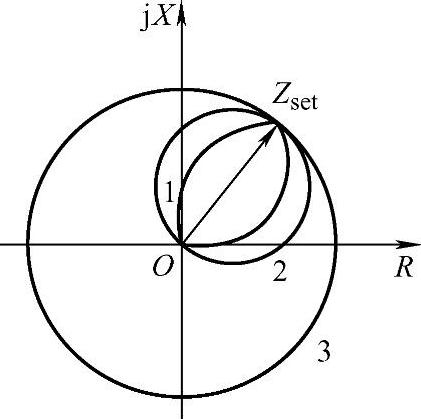
图3-15 阻抗特性图

图3-16 测量阻抗变化轨迹图
振荡中心在线路NP上距母线N75km处。保护1的Ⅱ段、保护3的Ⅰ段、保护4的Ⅰ段和Ⅱ段受振荡的影响。
(2)橄榄形动作特性阻抗继电器躲振荡能力最强,方向阻抗继电器其次,全阻抗继电器最差。
【例3-8】 (1)求图3-17a所示单侧110kV线路上保护1中阻抗元件的测量阻抗Zm,并绘制在复平面上。已知短路类型为两相短路,故障点过渡电阻R=4Ω,线路阻抗为(0.27+j0.41)Ω/km。短路点到保护1距离为10km。
(2)求图3-17b双侧电源110kV线路上保护1中阻抗元件的测量阻抗Zm,并绘制在复平面上。短路点到保护1的距离L、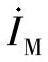 、
、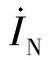 之值分3种方案列于表3-2中。其他已知条件同上。
之值分3种方案列于表3-2中。其他已知条件同上。
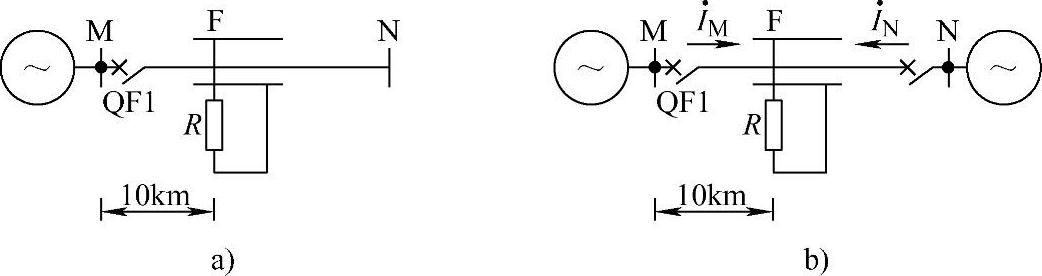
图3-17 例3-8示意图
表3-2 短路点到保护1的部分数据表

【解】 根据故障分析理论,两相经过渡电阻R短路,可看做在故障点接入各相具有R/2电阻的分支线上发生的金属性短路(以BC为例)。M侧保护1的测量阻抗为

式中,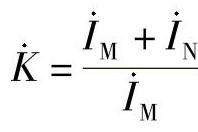 。
。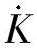 为复数,因此
为复数,因此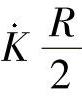 可能呈感性,也可能呈容性。由线路两侧电流相位关系可确定
可能呈感性,也可能呈容性。由线路两侧电流相位关系可确定 呈容性还是感性。对于单侧电源线路,因
呈容性还是感性。对于单侧电源线路,因 ,则
,则
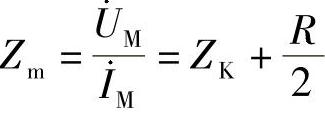
由上式可以看出,对于单侧电源线路,过渡电阻的存在必然使测量阻抗增大,保护范围缩小。在双侧电源线路上,过渡电阻存在可能使保护范围缩小,也可能使保护范围增大。
(1)单侧电源保护1的测量阻抗为

(2)双侧电源
方案
方案2: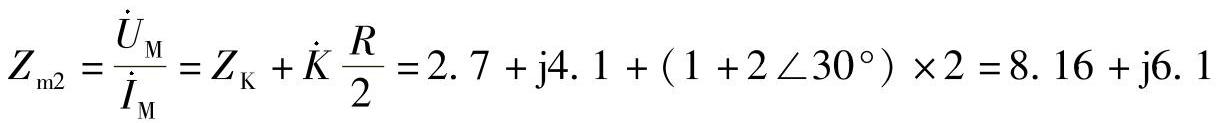
方案3:
计算结果如图3-18所示。
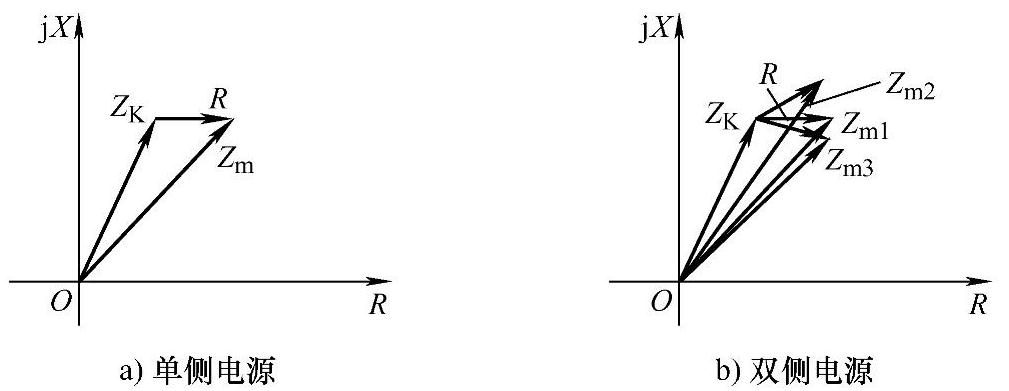
图3-18 测量阻抗图
【例3-9】 (1)若线路短路阻抗角φk=80°,整定时将圆特性方向阻抗元件的最大灵敏角整定为φsen=60°,对保护有何影响?
(2)当圆特性方向元件的最大灵敏角φsen不等于线路阻抗角时,是选择最大灵敏角φsen大于线路短路阻抗角φk,还是选择最大灵敏角φsen小于线路短路阻抗角φk?
(3)若最小负荷阻抗ZL.min=7∠30°Ω,线路阻抗角φk=60°时圆特性方向阻抗元件的整定阻抗Zset=8∠60°Ω,当测量阻抗角为30°时,该阻抗元件的动作阻抗为多少?
【解】 当方向元件测量阻抗Zm的阻抗角与正向整定阻抗角相等时,阻抗继电器的动作阻抗最大,继电器最灵敏。
(1)会使保护范围缩短,灵敏度降低。如图3-19所示,当测量阻抗整定阻抗角为60°时,动作阻抗为Zop=Zsetcos(80°-60°)=0.94Zset,显然动作阻抗小于整定阻抗。
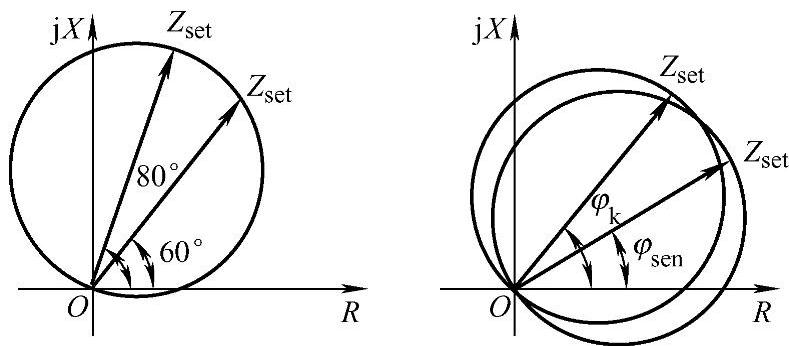
图3-19 整定阻抗角与最大灵敏角不相等
(2)当φsen<φk时,能够增加距离保护躲过渡电阻能力,方向元件在+R轴方向有更大动作区,躲过渡电阻能力强。
(3)当测量阻抗角为30°时,该方向元件的动作阻抗为Zop=8cos30°=6.93Ω。
【例3-10】 若阻抗元件整定阻抗为Zset=10∠75°Ω,写出其绝对值比较动作方程和相位比较动作方程。已知其动作特性为:(1)全阻抗特性;(2)方向圆特性。
【解】 (1)绝对值比较动作方程:Zm≤10
相位比较动作方程: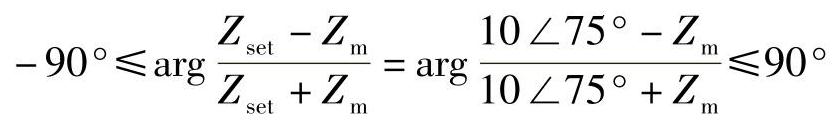
(2)绝对值比较动作方程:Zm-5∠75°≤5
相位比较动作方程: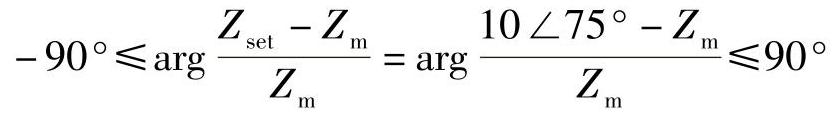
【例3-11】 分别用绝对值比较原理和相位比较原理写出图3-20中动作特性圆的动作方程式(圆内为动作区,圆外为非动作区)。
【解】 图3-20a的绝对值比较动作方程为|Zm+0.5j(XA+XB)|≤|0.5j(XB-XA)|;相位比较方程为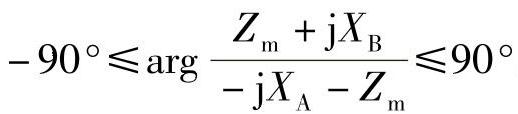 。
。
图3-20b的绝对值动作方程为|Zm-0.5j(XA-XB)|≤|0.5j(XA+XB)|;相位比较方程为 。
。
【例3-12】 如图3-21所示的双侧电源网络,参数如图中所示,已知 。求线路MN两侧距离保护的Ⅰ段整定值,并指出图中F点经过渡电阻三相短路时,线路MN两侧距离保护Ⅰ段能否正确动作(测量元件采用圆特性方向阻抗元件,KⅠrel=0.8)?
。求线路MN两侧距离保护的Ⅰ段整定值,并指出图中F点经过渡电阻三相短路时,线路MN两侧距离保护Ⅰ段能否正确动作(测量元件采用圆特性方向阻抗元件,KⅠrel=0.8)?
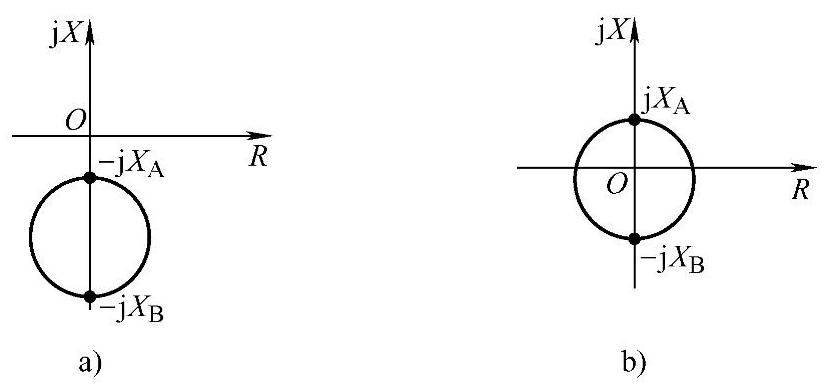
图3-20 例3-11动作特性圆
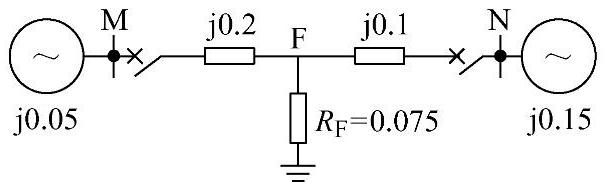
图3-21 例3-12系统接线图
【解】 MN两侧距离保护Ⅰ段整定值为ZⅠsetM=ZⅠsetN=j0.24;短路点短路电流为
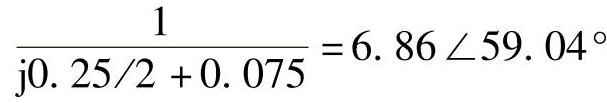 、短路点电压为Uk=I(3)kRF=0.515∠59.04°。MN两侧的测量电流均为3.43∠59.04°。
、短路点电压为Uk=I(3)kRF=0.515∠59.04°。MN两侧的测量电流均为3.43∠59.04°。
M侧距离保护的测量阻抗
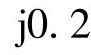 。N侧距离保护的测量阻抗
。N侧距离保护的测量阻抗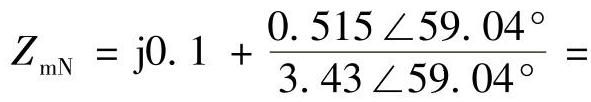
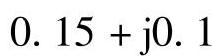 。在复平面上画出线路MN两侧方向元件的动作特性及测量阻抗如图3-22所示,由图3-22可知,两侧距离保护Ⅰ段均拒动。
。在复平面上画出线路MN两侧方向元件的动作特性及测量阻抗如图3-22所示,由图3-22可知,两侧距离保护Ⅰ段均拒动。

图3-22 两侧测量阻抗图
【例3-13】 双侧电源115kV电压等级的网络如图3-23所示。已知:线路正序阻抗Z1=0.4Ω/km,阻抗角φL1=75°;在保护1~4均装设距离保护,其Ⅰ、Ⅱ段阻抗测量元件采用圆特性方向阻抗元件,起动元件采用电流元件(Iset=4A,nTA=200);KⅠrel=KⅡrel=0.85。当系统发生振荡时,分析保护1阻抗测量元件和起动元件误动作的可能性。
【解】 保护1的整定值为
ZⅠset1=0.85×0.4×100Ω=34Ω
ZⅠset3=0.85×0.4×150Ω=51Ω
ZⅡset1=0.85ZⅠset3=43.35Ω
振荡中心在线路NP距N侧12.5km处,显然处于保护1的Ⅰ段保护区外,不会误动作,而Ⅱ段可能误动作。

图3-23 例3-13系统接线图
系统振荡时,流过保护1的电流为 ,当δ=180°时,
,当δ=180°时,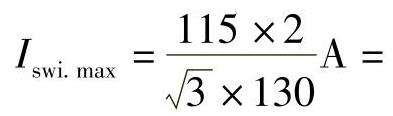
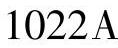 ,二次值为
,二次值为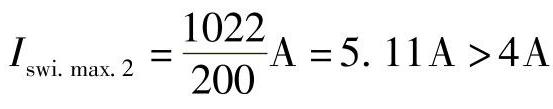 ,起动元件可能误动作。
,起动元件可能误动作。
【例3-14】 如图3-24所示双侧电源线路MN,设 ,且全系统阻抗角相等,求下列情况下,安装于M侧、N侧的距离保护1和2的测量阻抗。
,且全系统阻抗角相等,求下列情况下,安装于M侧、N侧的距离保护1和2的测量阻抗。
(1)系统正常运行时;
(2)线路MN的N侧正方向出口三相短路时;
(3)系统发生振荡且振荡角δ=180°时。
【解】 (1)因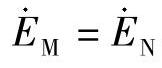 ,距离保护1、保护2的测量阻抗为Zm1=Zm2=∞。
,距离保护1、保护2的测量阻抗为Zm1=Zm2=∞。
(2)保护1的测量阻抗为Zm1=j0.3Ω、保护2的测量阻抗为Zm2=0Ω。
(3)系统振荡且振荡角δ=180°时,相当于在振荡中心发生三相短路,振荡中心处于离M侧j0.2Ω(相当于2/3处),因此保护1测量阻抗Zm1=j0.2Ω,保护2测量阻抗Zm2=0.1Ω。
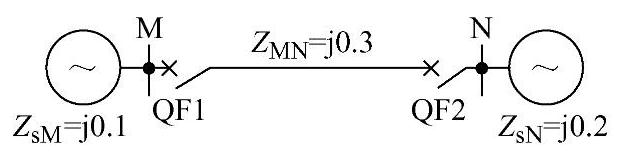
图3-24 例3-14系统接线图
【例3-15】 系统接线如图3-25所示,发电机以发电机变压器组方式接入,最大开机方式为4台机全开,最小开机方式为两侧各开一台,变压器T5和T6可能2台也可能1台运行。其参数如下: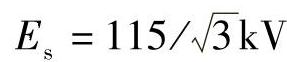 ,发电机G1、G2容量相等,X1.G1=X1.G2=X2.G1=X2.G2=15Ω、发电机G3、G4容量相等,X1.G3=X2.G3=X1.G4=X2.G4=10Ω;1~4号变压器的正序阻抗X1T=10Ω,变压器零序阻抗X0T=30Ω;5~6号变压器正序阻抗X1T=20Ω,变压器零序阻抗X0T=40Ω;线路阻抗Z1=0.4Ω/km,零序阻抗Z0=1.2Ω/km;全系统阻抗角均为75°;KⅠrel=0.85,KⅡrel=0.75,变压器均装有快速差动保护。求:
,发电机G1、G2容量相等,X1.G1=X1.G2=X2.G1=X2.G2=15Ω、发电机G3、G4容量相等,X1.G3=X2.G3=X1.G4=X2.G4=10Ω;1~4号变压器的正序阻抗X1T=10Ω,变压器零序阻抗X0T=30Ω;5~6号变压器正序阻抗X1T=20Ω,变压器零序阻抗X0T=40Ω;线路阻抗Z1=0.4Ω/km,零序阻抗Z0=1.2Ω/km;全系统阻抗角均为75°;KⅠrel=0.85,KⅡrel=0.75,变压器均装有快速差动保护。求:
(1)为了快速切除线路故障,线路MN、NP应在何处配置三段式距离保护,各选用何种接线?选用何种动作特性?
(2)整定保护1~4的距离Ⅰ段,并按照选定的动作特性,在一个阻抗平面上画出各保护的动作区域。
(3)分别求出保护1、4接地距离Ⅱ段的最大、最小分支系数。
(4)求保护1接地距离Ⅱ段的整定值及灵敏度。
(5)当线路MN中点处发生BC两相接地短路时,哪些保护的测量元件动作。保护和断路器正常情况下应什么时间断开哪些断路器?
(6)短路条件同(5),若保护1的接地距离拒动、保护2处断路器拒动,哪些保护以什么时间断开哪些断路器?
【解】 1.计及双侧电源时
(1)为了快速切除线路上各种短路故障,线路MN、NP应在断路器1~4处分别配置三段式相间距离和接地距离保护。相间距离保护用于切除相间故障,采用接入故障相线电压和故障相两相电流差的接线方式。接地距离保护用于切除接地故障,采用接入故障相电压和零序电流补偿的故障相电流的接线方式。距离保护Ⅰ、Ⅱ、Ⅲ段可采用多边形特性,其中Ⅲ段带有偏移特性。或者Ⅰ、Ⅱ、Ⅲ段采用由方向阻抗特性和电抗特性经“与”关系组成。通常还配有快速距离Ⅰ段和带延时的距离Ⅰ段和Ⅱ段(反应振荡过程的故障)。
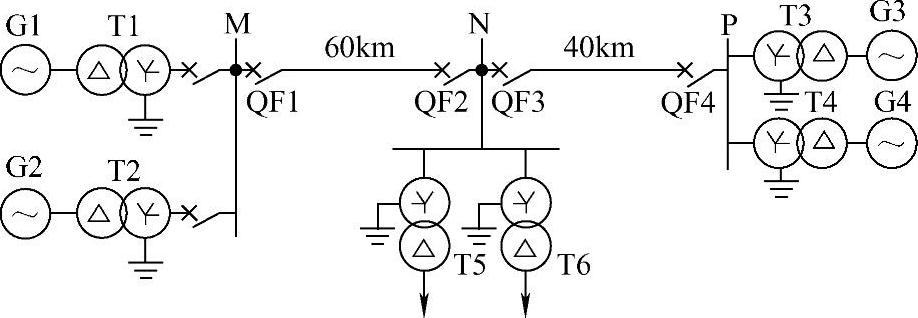
图3-25 例3-15系统接线图
(2)保护1、2的距离Ⅰ段整定值为
ZⅠset1=ZⅠset2=0.85×0.4×60∠75°Ω=20.4∠75°Ω
保护3、4的距离Ⅰ段整定值为
ZⅠset3=ZⅠset4=0.85×0.4×40∠75°Ω=13.6∠75°Ω
保护1、保护3的距离Ⅰ段动作区域特性如图3-26所示,保护2和保护4与保护1、保护3相同。
(3)接地距离保护1和保护4的正序电流分支系数Kb1=Kb4=1,即正序不存在助增或汲出。
当M侧开一台机器,变压器T5和T6均投入运行,保护1零序电流分支系数最大;当M侧机组全开,变压器T5和T6只有一台投入运行,保护1的零序电流分支系数最小。
保护1的最大分支系数为
保护1的最小分支系数为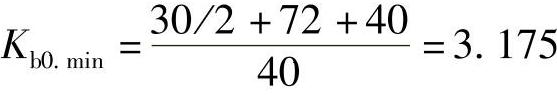
保护4的最大分支系数为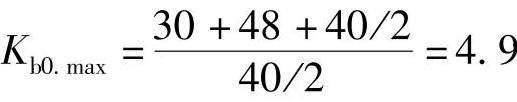
保护4的最小分支系数为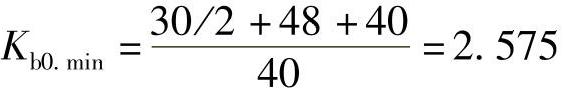
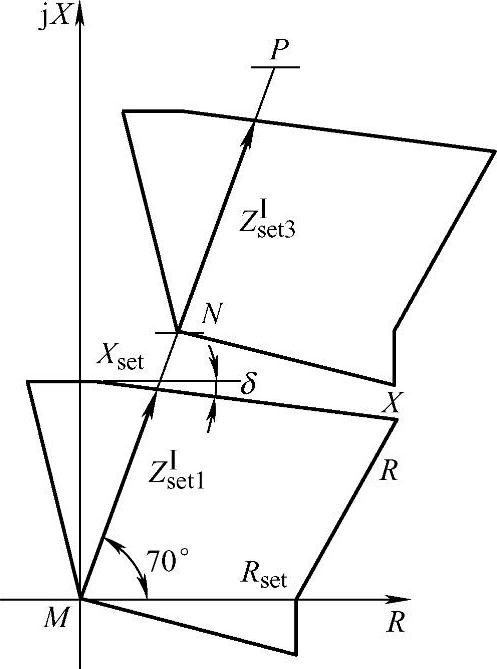
图3-26 距离Ⅰ段动作特性图
(4)利用故障分析理论,如图3-27所示,可计算在保护3的Ⅰ段保护范围末端发生单相接地故障时,流过保护1的零序电流。
1)两侧系统最大运行方式下保护3的Ⅰ段保护范围末端发生单相接地故障,系统总正序、零序等效正序电抗为
M侧至故障点的正序电抗:(12.5+24+0.85×16)Ω=(36.5+13.6)Ω=50.1Ω
正序总电抗:XΣ1=(50.1//12.4)Ω=9.94Ω
M侧至故障点的零序电抗:[(15+72)//20+0.85×48]Ω=(16.26+40.8)Ω=57.06Ω
零序总电抗:XΣ0=(57.06//22.2)Ω=15.98Ω
流过保护3的零序电流: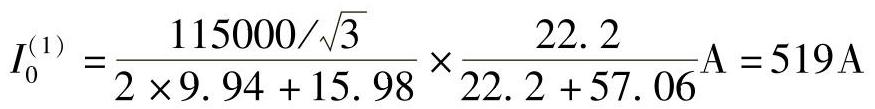
流过保护1的零序电流: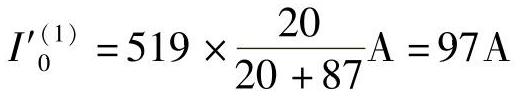
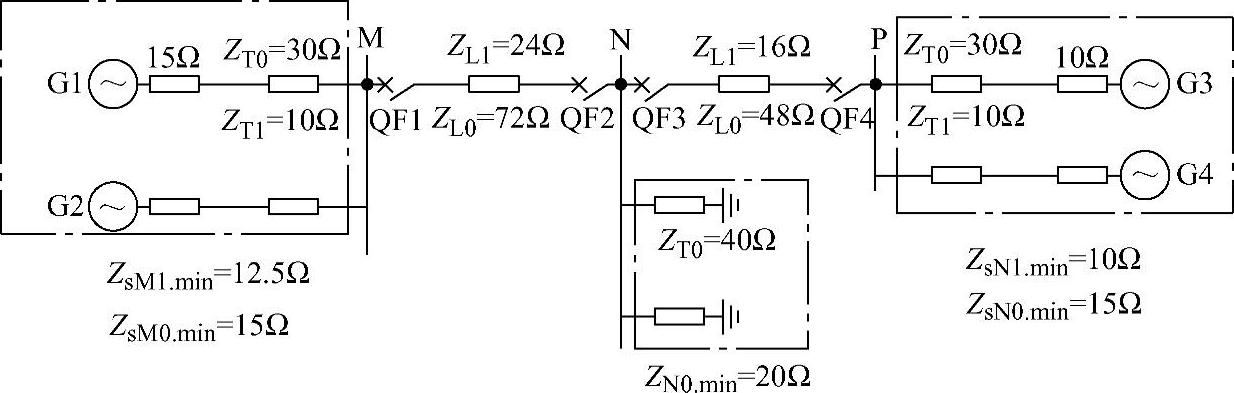
图3-27 系统阻抗图
2)P侧系统处于最小运行方式,在保护3的Ⅰ段保护范围末端发生单相接地故障时,流过保护1的零序电流。
M侧至故障点的正序电抗:12.5Ω+24Ω+0.85×16Ω=(36.5+13.6)Ω=50.1Ω
正序总电抗:XΣ1=(50.1//22.4)Ω=15.48Ω
M侧至故障点的零序电抗:(15+72)//20Ω+0.85×48Ω=16.26Ω+40.8Ω=57.06Ω
零序总电抗:XΣ0=(57.06//37.2)Ω=22.52Ω
流过保护3的零序电流:
流过保护1的零序电流: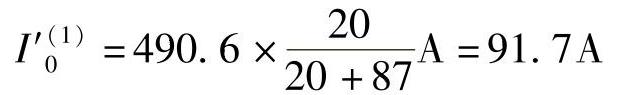
3)母线N变压器一台接地、P侧系统处于最小运行方式时。
M侧至故障点的正序电抗:(12.5+24+0.85×16)Ω=(36.5+13.6)Ω=50.1Ω
正序总电抗:XΣ1=(50.1//22.4)Ω=15.48Ω
M侧至故障点的零序电抗:(15+72)//40Ω+0.85×48Ω=27.40Ω+40.8Ω=68.2Ω
零序总电抗:XΣ0=(68.2//37.2)Ω=24.07Ω
流过保护3的零序电流:
流过保护1的零序电流: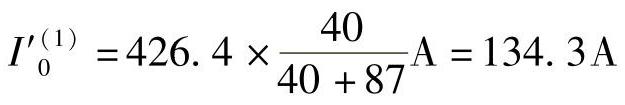
4)母线N变压器一台接地、P侧系统处于最大运行方式时。
M侧至故障点的正序电抗:(12.5+24+0.85×16)Ω=(36.5+13.6)Ω=50.1Ω(https://www.xing528.com)
正序总电抗:XΣ1=(50.1//12.4)Ω=9.94Ω
M侧至故障点的零序电抗:(15+72)//40Ω+0.85×48Ω=27.40Ω+40.8Ω=68.2Ω
零序总电抗:XΣ0=(68.2//22.2)Ω=16.75Ω
流过保护3的零序电流: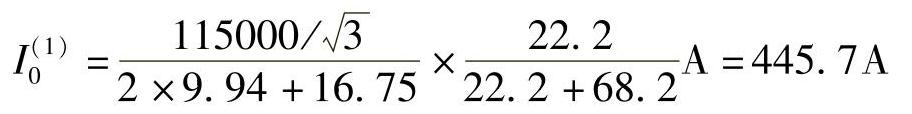
流过保护1的零序电流: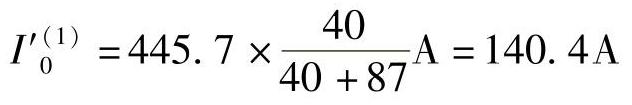
从计算可知,M侧系统应取最大运行方式,P侧系统应取最大运行方式,母线N变压器一台接地时流过保护1的零序电流最大。
在此运行状态下,流过保护1的正序、负序电流为

故障相电流(考虑三序相位相同)为
Ip=(2×360+140.4)A=860.4A
零序补偿系数为
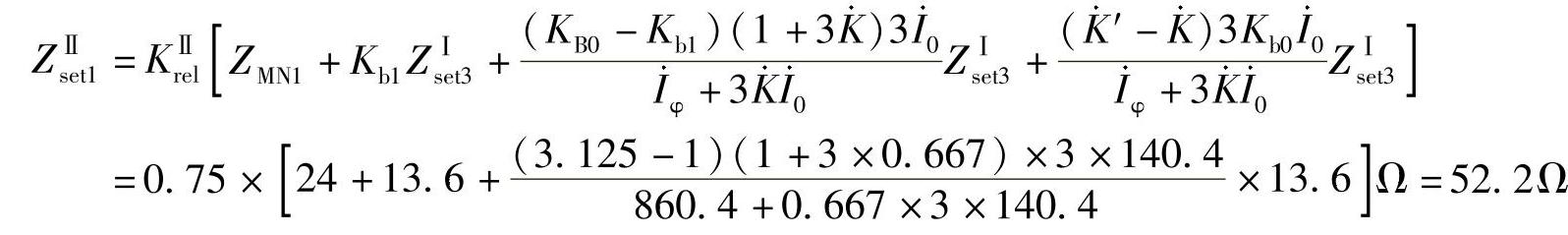
2.仅计及M侧电源时
计算阻抗图如图3-28所示。
1)母线N变压器两台同时接地时。
正序总电抗:(12.5+24+13.6)Ω=50.1Ω
零序总电抗:(15+72)//20Ω+40.8Ω=16.26Ω+40.8Ω=57.06Ω
流过保护3的零序电流: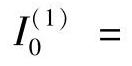

流过保护1的零序电流:

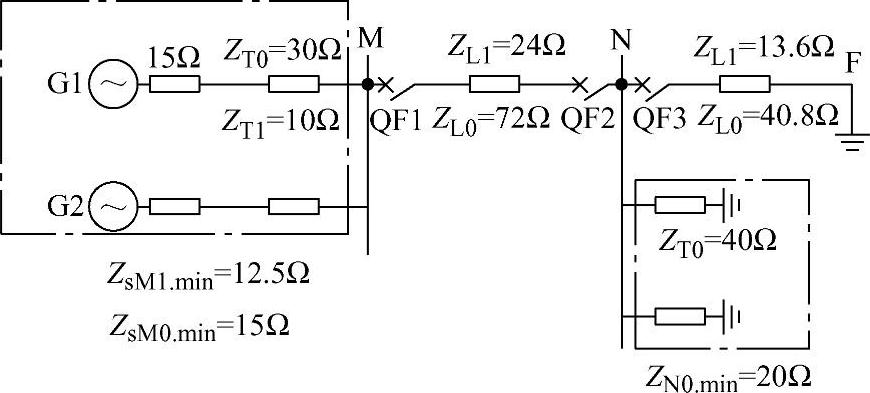
图3-28 仅M侧电源阻抗图
2)母线N变压器单台接地时。
正序总电抗:(12.5+24+0.85×16)Ω=50.1Ω
零序总电抗:(15+72)//40Ω+0.85×48Ω=27.4Ω+40.8Ω=68.20Ω
流过保护3的零序电流: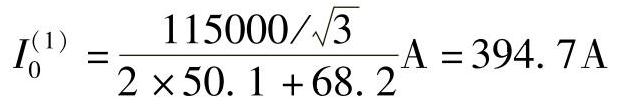
流过保护1的零序电流:
流过保护1的相电流:Ip=2I1+I0=913.7A
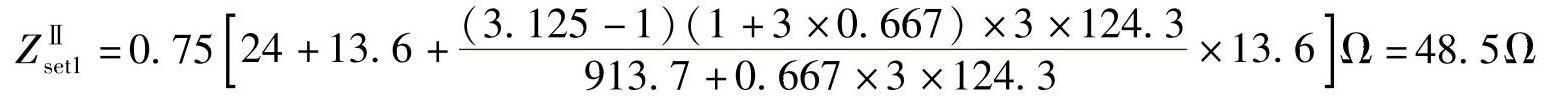
由上面的计算过程可知,仅计单侧电源时与双侧电源同时作用时的计算结果相近,但仅计算单侧电源存在误差。
灵敏度校验: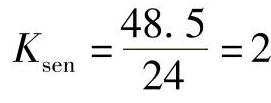
当线路MN中点处发生BC两相接地短路时,测量元件动作的有:保护1和保护2的相间距离保护和接地距离保护的Ⅰ、Ⅱ、Ⅲ段,保护4的相间距离保护Ⅲ段和接地距离保护的Ⅱ、Ⅲ段。保护、断路器正常工作情况下,保护1和保护2的Ⅰ段经固有动作时间断开断路器QF1和QF2,从而切除故障。
保护1相间距离Ⅰ段断开QF1,保护4的接地距离保护Ⅲ段断开QF4切除故障。
【例3-16】 如图3-29所示网络,全系统阻抗角为80°,ZⅠset1=24Ω,ZⅡset1=32Ω,tⅡ1=0.4s。系统振荡周期T=0.9s。求:
(1)双侧电源电动势相同,求系统振荡中心的位置?
(2)线路NP、PQ的保护是否应加装振荡闭锁,为什么?
(3)距离保护1的Ⅰ、Ⅱ段采用圆特性方向阻抗特性,是否加装振荡闭锁装置。
【解】 (1)振荡中心在线路MN中点。
(2)线路NP、PQ保护不加装振荡闭锁。振荡过程中,虽然母线N、P、Q的电压会出现周期性变化,但母线N的电压幅值不大于电动势。单电源线路电流虽然也会出现周期性变化,但不会使电流保护起动。若单电源线路装有距离保护,由于母线电压和线路电流的变化趋势一致,所以测量元件测量到的阻抗不变,保护也不会起动。
(3)振荡过程中,距离保护1第Ⅰ段会误动,需要装设闭锁装置。对于距离保护1的Ⅱ段,由图3-30可得,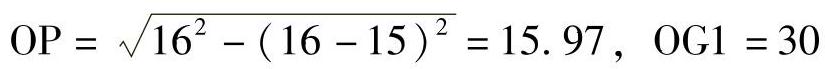 ,则系统振荡时,保护1的第Ⅱ段误动作的角度为
,则系统振荡时,保护1的第Ⅱ段误动作的角度为 。在最短振荡周期下误动时间为t=0.9×
。在最短振荡周期下误动时间为t=0.9× ,所以距离保护1的第Ⅱ段不需加装振荡闭锁装置。
,所以距离保护1的第Ⅱ段不需加装振荡闭锁装置。
【例3-17】 系统保护配置同【例3-16】,保护1的Ⅰ、Ⅱ段采用方向阻抗特性,EM=EN,分析在距离母线M20Ω处发生经15Ω过渡电阻短路时,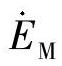 超前
超前 角度为0°的条件下,保护1的Ⅰ、Ⅱ段动作情况。
角度为0°的条件下,保护1的Ⅰ、Ⅱ段动作情况。
【解】 当 与
与 同相位时,流入短路点电流为
同相位时,流入短路点电流为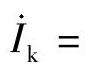
 ;流过保护1的电流为
;流过保护1的电流为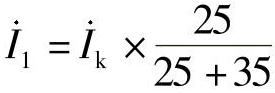 ,保护1的测量电压为
,保护1的测量电压为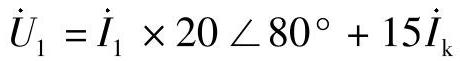 ,保护1测量阻抗为
,保护1测量阻抗为
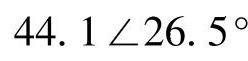 。当角度为26.5°,保护1的Ⅰ段动作阻抗为14.28Ω,保护1的Ⅱ段动作阻抗为19.03Ω,所以保护1的Ⅰ、Ⅱ段将拒动。
。当角度为26.5°,保护1的Ⅰ段动作阻抗为14.28Ω,保护1的Ⅱ段动作阻抗为19.03Ω,所以保护1的Ⅰ、Ⅱ段将拒动。

图3-29 例3-16系统接线图
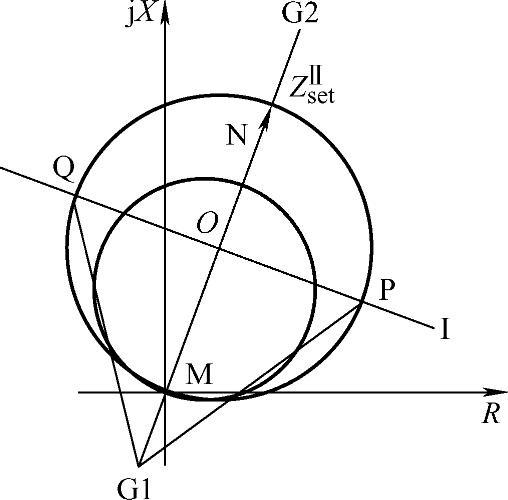
图3-30 振荡误动计算图
【例3-18】 如图3-31所示,线路MN和NP上分别装设阶段式距离保护1和2。已知接入保护的电流互感器变比(电流比)为2000/5,电压互感器变比(电压比)为110000/100。线路阻抗Z1=0.4Ω/km,KⅠrel=KⅡrel=0.8。求:
(1)当线路MN和NP的长度分别为100km和20km,距离保护1的Ⅰ、Ⅱ段的二次整定阻抗值,并校验Ⅱ段的灵敏度。
(2)当线路MN和NP的长度分别为20km和100km,距离保护1的Ⅰ、Ⅱ段的二次整定阻抗值,并校验Ⅱ段的灵敏度。
(3)分析比较上述两种情况的灵敏度,可得出什么结论?
【解】 (1)保护1的Ⅰ段整定值ZⅠset1=0.8×0.4×100Ω=32Ω,保护2的Ⅰ段整定值ZⅠset2=0.8×0.4×20Ω=6.4Ω,保护1的Ⅱ段整定值ZⅡset1=0.8×(40+6.4)Ω=37.12Ω,灵敏度 。二次值计算:保护1的二次值为
。二次值计算:保护1的二次值为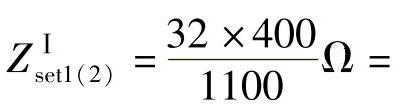
 、
、 。
。

图3-31 例3-18系统接线图
(2)保护1的Ⅰ段整定值ZⅠset1=0.8×0.4×20Ω=6.4Ω,保护2的Ⅰ段整定值ZⅠset2=0.8×0.4×100Ω=32Ω,保护1的Ⅱ段整定值ZⅡset1=0.8×(8+32)Ω=32Ω,灵敏度
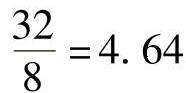 。二次值计算:保护1的二次值为
。二次值计算:保护1的二次值为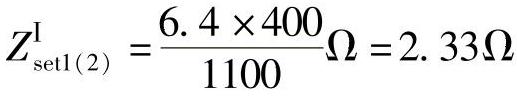 、
、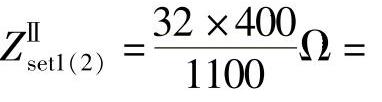
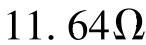 。
。
(3)短线路距离保护的Ⅱ段灵敏度可能出现不满足要求,所以短线路上使用距离保护不易配合,而长线路上不存在此问题。
【例3-19】 如图3-32所示,试对保护1进行三段式电流保护的整定计算,已知流过线路MN的最大负荷电流为170A,线路阻抗Z1=0.4Ω/km,KⅠrel=1.3,KⅡrel=1.1,KⅢrel=1.2,Kre=0.85,Δt=0.5s。
【解】 (1)保护1的Ⅰ段。

动作电流:
IⅠop1=1.3×6647A=8642A
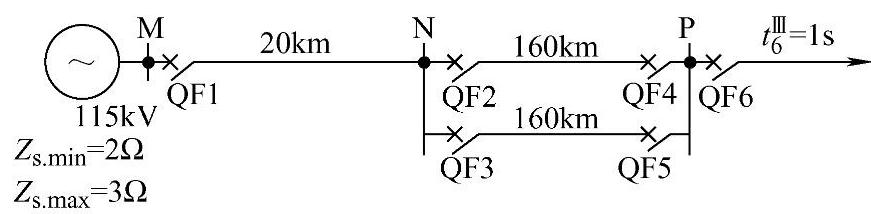
图3-32 例3-19系统接线图
最小保护区为 ,解之Zx=3.65Ω。
,解之Zx=3.65Ω。
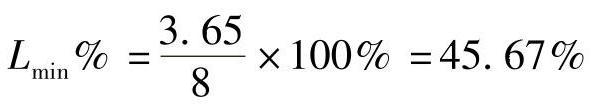
(2)保护1的Ⅱ段。
相邻线路单回路运行时:
保护2的Ⅰ段:IⅠop1=1.3×898.3A=1167.8A
动作电流:IⅡop1=1.1×1167.3A/0.5=2569.2A
相邻线路并列运行时最大短路电流:
动作电流:IⅡop1=1.1×1.3×1582.7A=2263.3A,动作电流取IⅡop1=2569.2A。
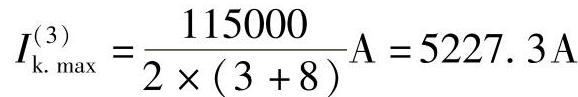 ,灵敏度
,灵敏度 。
。
(3)保护1的Ⅲ段。
动作电流:
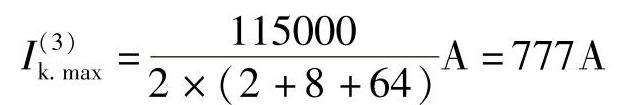
近后备灵敏度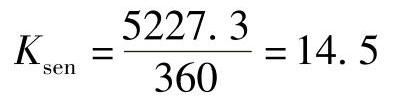
远后备灵敏度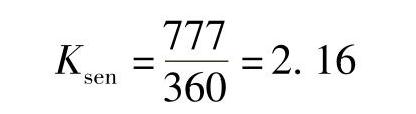
【例3-20】 WXB-11线路距离整定值清单含义是什么?
整定值清单见表3-3。
表3-3 WXB—11线路距离整定值清单
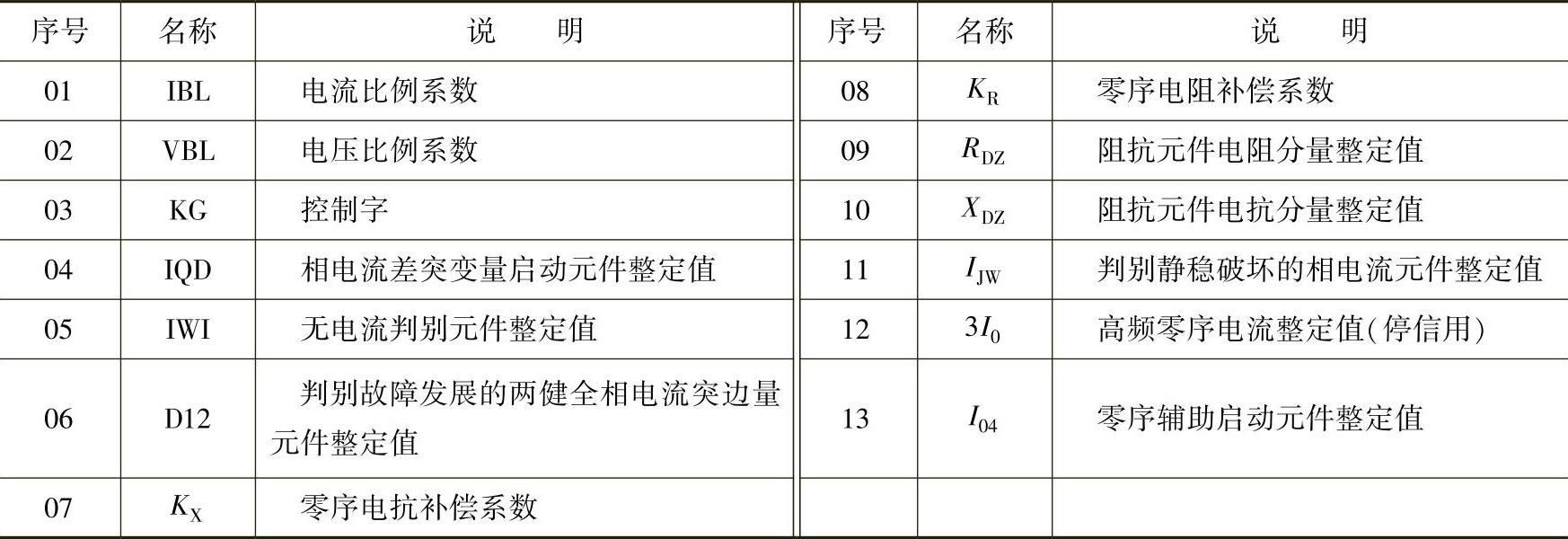
【解】 (1)第1、2项为电流、电压比例系数。由于采用VFC模-数转换器,其转换结果用固定时间内(KTs)计数器所计脉冲个数表示。对于额定电流为5A的装置而言,电流变换器二次侧只有一个电阻时,保护工作范围为0.5~100A,当K=2时,IBL=0.177;电流变换器副方有两个电阻时,保护工作范围为1~200A,当K=2时,IBL=0.356。
同理,VBL是单位脉冲所代表的电压值,当K=2时,VBL=0.125。上述两项比例系数由厂家提供,用户不应改变。
(2)KG为控制字,用于改变保护方案。
(3)IQD为相电流差突变量启动元件整定值,改变整定值应满足在最小运行方式下保护范围末端故障时有足够的灵敏度。
(4)IWI作用是:一是在发出跳闸命令后,判别故障是否切除;二是在发出合闸命令后,用于判断断路器是否合上,以便开始重合后加速阻抗计算。整定值只要保证重合到永久性故障时有足够的灵敏度,并且应躲开线路充电电容电流的稳态值。
(5)D12的整定原则是按本线路在非全相运行期间发生故障时有足够的灵敏度。
(6)零序补偿系数
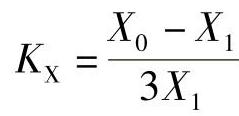 ,
, 。式中数值应取线路的实测值。
。式中数值应取线路的实测值。
(7)由多边形阻抗元件特性可见,只有电阻、电抗分量可以整定,如图3-33所示。
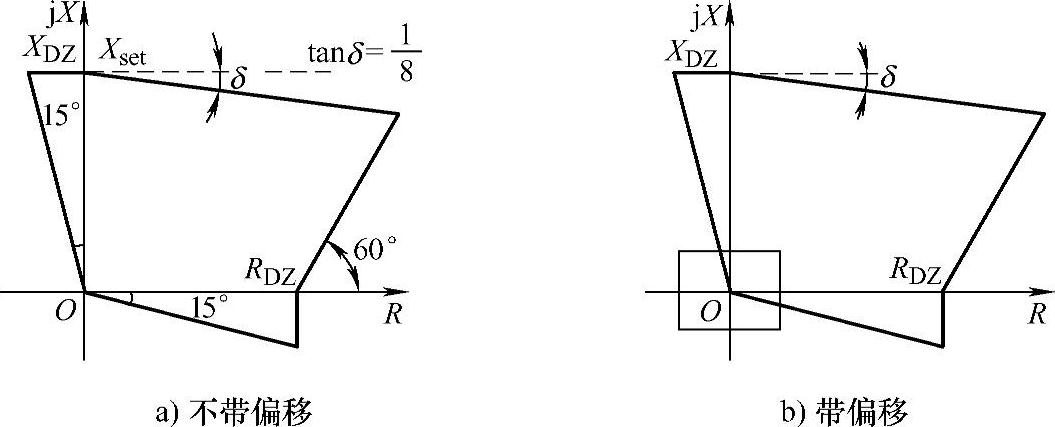
图3-33 多边形阻抗元件特性图
整定方法可用图3-34说明,其中φ1为线路阻抗角;Zset为φ1方向的整定阻抗值;Zloa为负荷阻抗;φloa为负荷阻抗角。
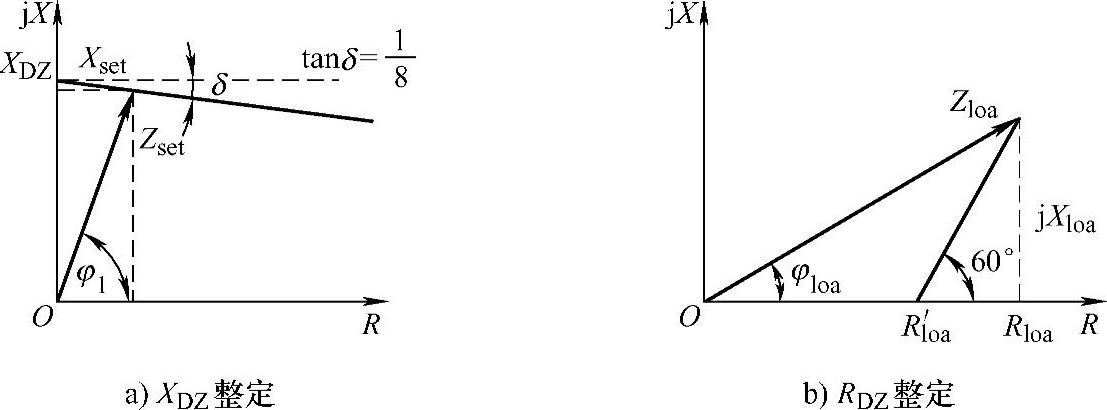
图3-34 阻抗元件整定说明图
由图3-34可得
XDZ=Zsetsinφ1+Zsetcosφ1tanδ
电阻值反映了保护的耐电弧能力,当RDZ越大时,耐电弧能力越强,而RDZ越小,对躲开系统振荡越有利。RDZ的整定原则是:躲开负荷阻抗的电阻分量,且线路末端故障时有足够的灵敏度。过负荷阻抗Zloa末端作与R轴成60°的直线,得R′loa,则
RDZ=(0.7~0.8)R′loa
该阻抗元件的主要作用:一是作为高频距离保护的阻抗方向判别元件;二是作为转换性故障的阻抗确认元件;三是作为手合及重合闸后加速阻抗元件;四是作为振荡停息的判别元件。
偏移特性是在方向特性的基础上叠加一个小矩形,构成“或”逻辑,从而使动作特性包含了原点,保证正方向出口故障可靠动作。
(8)IJW的整定原则是躲开最大负荷电流。
(9)3I0的整定原则是保证线路末端接地故障时有足够灵敏度。该元件动作是高频零序方向保护停信的条件之一,另一条件为零序方向元件,而零序方向元件的3U0固定为1V,在整定值中未列出。
(10)I04零序辅助启动元件整定的很灵敏,动作后驱动会快速启动继电器。
【例3-21】 如图3-35所示,某多边形元件由三部分组成:电抗元件、电阻元件和方向元件,试说明各边倾斜的目的是什么?
【解】OA左倾α2是为了在保护区发生金属性短路故障时保护能够可靠动作。当保护范围内发生金属性短路故障时,测量阻抗应为线路阻抗角,但实际上由于互感器和保护装置都有误差,使测量阻抗偏离线路阻抗角。
直线DC下倾δ是为了在双电源线路上防止相邻线路出口经过电阻接地时的超越。
直线OB下倾α1是为了在本线路出口经过渡电阻接地时,保护可靠动作。
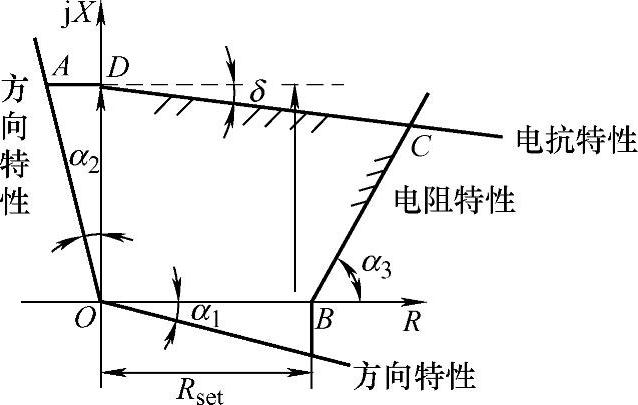
图3-35 多边阻抗继电器动作特性图
要求α3小于线路阻抗角是为了提高长线路避越重负荷阻抗的能力。
【例3-22】 已知多边形阻抗元件的动作特性如图3-36所示,其中α1=α2=14°,α3=60°,δ=7.1°,Xset=30Ω,Rset=120Ω。试分析当测量阻抗为以下数值时阻抗元件是否动作?
(1)Zm=30∠60°Ω;(2)Zm=180∠30°Ω;(3)Zm=36∠45°Ω。
【解】 将测量阻抗Zm画在复平面上,如图3-36所示,过Zm点作BC和CD的平行线,分别与R轴、jX轴交于点D1和点B1。
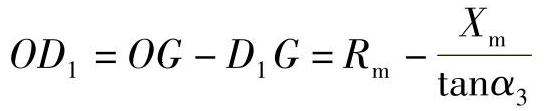
OB1=OF+B1F=Xm+Rmtanδ
由图3-36可见,测量阻抗Zm=Rm+jXm落入动作区内的判据为同时满足:

(1)Zm=30∠60°=15+j25.98,Rm=15Ω,Xm=25.98Ω
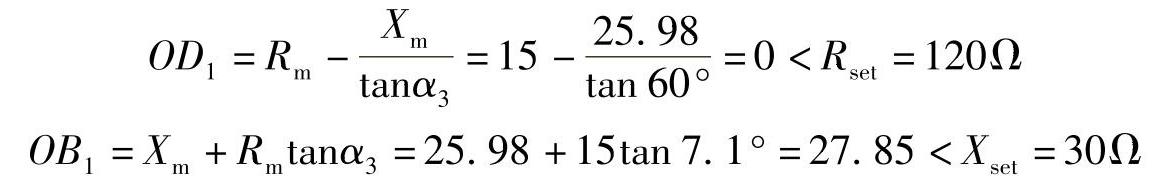
因此当Zm=30∠60°Ω时,该阻抗元件动作。

图3-36 多边形阻抗特性图
(2)当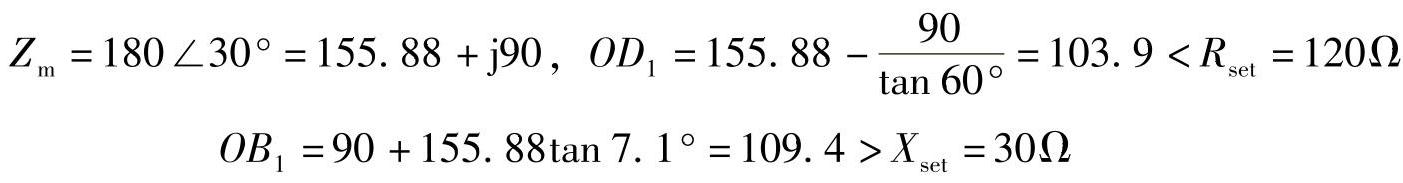
所以,当Zm=180∠30°Ω时,该阻抗元件不动作。
(3)当

所以,当Zm=36∠45°Ω时,该阻抗元件动作。
【例3-23】 某线路的相间距离保护Ⅰ段采用如图3-37所示多边形特性的阻抗元件作为测量元件,图中α1=α2=14°,α3=60°,tanδ=1/8。线路额定电压为110kV,保护范围为100km,线路阻抗为(0.27+j0.41)Ω/km。线路最大负荷电流IL.max=250A,最大负荷阻抗角φL.max=30°。已知Krel=1.2,Kss=1.3。试求该阻抗元件的整定值Rset和Xset。
【解】 多边形特性阻抗元件的整定和圆特性阻抗元件的整定有所不同。图3-37准四边形特性阻抗元件可以独立整定Rset和Xset。Rset、Xset和阻抗元件整定值Zset、最小负荷阻抗ZL.min之间的关系可根据图3-38用几何方法得到。
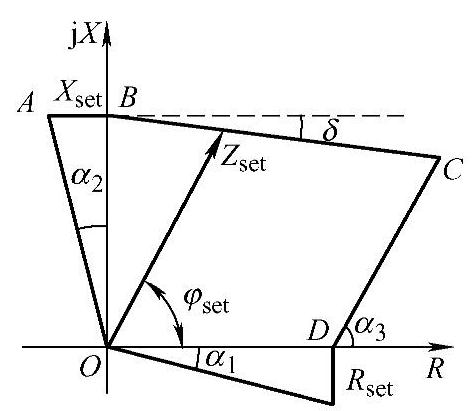
图3-37 动作特性图
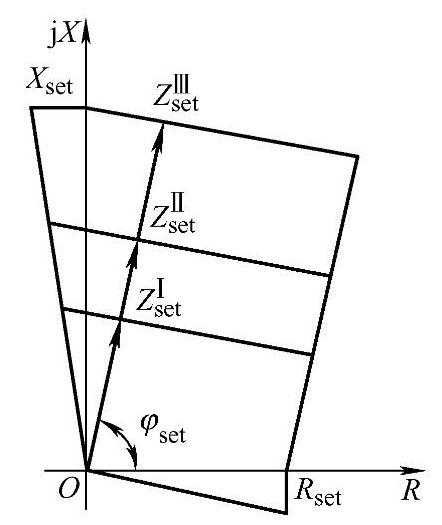
图3-38 三段式多边形阻抗元件特性图
Xset与圆特性元件整定值Zset之间的关系见图3-39,关系式为
Xset=|Zset|(sinφset+tanδcosφset) (3-1)
Rset按最小负荷阻抗整定。对于三段式距离保护,三段共用一个Rset,即
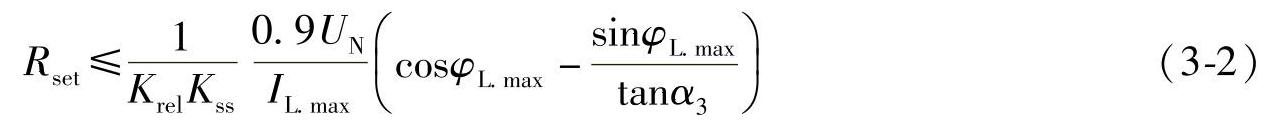
先计算Zset:Zset=100×(0.27+j0.41)=27+j41
利用式(3-1)计算Xset:
Xset=|Zset|(sinφset+tanδcosφset)=49.09×(sin56.63°+0.125×cos56.63°)=44.37Ω
其中: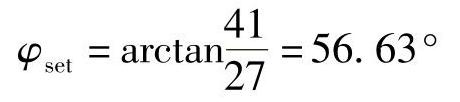
利用式(3-2)计算Rset:
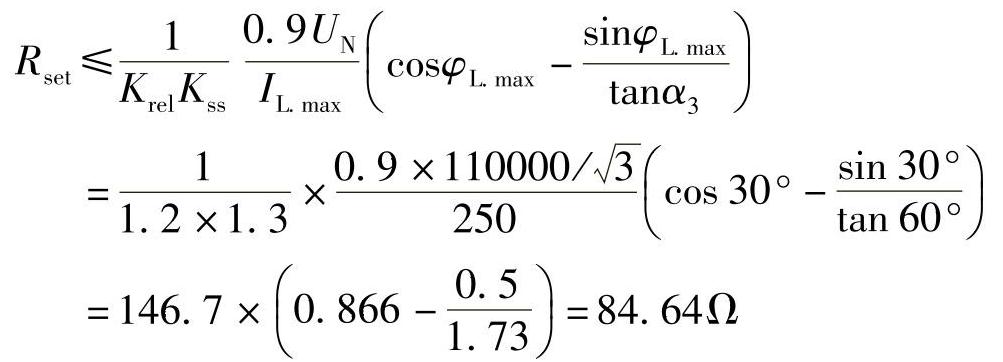

图3-39 Xset与圆特性元件整定值Zset之间关系图
【例3-24】 在微机保护装置中要实现方向元件的功能,已知整定阻抗为Zset=(7.11+j12.3)Ω,保护安装处的测量电压 和测量电流
和测量电流 已用傅里叶算法求得,分别为
已用傅里叶算法求得,分别为 和
和 。试采用数字式保护的相位比较实现方法判断该方向元件是否动作。
。试采用数字式保护的相位比较实现方法判断该方向元件是否动作。
【解】 在微机保护中,相位比较是实现阻抗元件的一种方法,既可以用阻抗的形式实现,也可以用电压的形式实现。用电压比较的方式又可分为相量比较方式和瞬时采样值比较两种。
相量比较方式步骤如下:
(1)根据阻抗元件的动作特性求出要进行相位比较的两个相量 和
和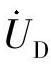 。若方向阻抗元件的动作方程为
。若方向阻抗元件的动作方程为 ,
,
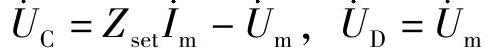
(2)将 和
和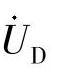 写成直角坐标形式,即
写成直角坐标形式,即 ,
,
(3)判断UCRUDR+UCIUDI≥0是否成立。若成立,则满足动作条件;否则,不满足动作条件。
(4)
UCRUDR+UCIUDI=-3530×3535.8-13170×1804.56<0,不满足要求,该阻抗方向元件不动作。
【例3-25】 如图3-40所示,对三段式接地距离保护1的Ⅰ段、Ⅱ段进行整定计算。阻抗测量元件用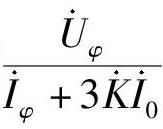 接线方式,正序分支系数Kb1=1.29,KⅠrel=KⅡrel=0.7。变压器归算至230kV的阻抗ZT=44.49Ω。线路参数:ZMN0=28.44Ω、ZMN1=11.45Ω;ZNP0=20.15Ω、ZNP1=7.39Ω。系统正序、零序阻抗角相等,系统M侧零序阻抗ZMs0=7.125Ω。在保护3的Ⅰ段范围末端发生单相接地短路时,保护1处测量到的故障相电流
接线方式,正序分支系数Kb1=1.29,KⅠrel=KⅡrel=0.7。变压器归算至230kV的阻抗ZT=44.49Ω。线路参数:ZMN0=28.44Ω、ZMN1=11.45Ω;ZNP0=20.15Ω、ZNP1=7.39Ω。系统正序、零序阻抗角相等,系统M侧零序阻抗ZMs0=7.125Ω。在保护3的Ⅰ段范围末端发生单相接地短路时,保护1处测量到的故障相电流 、
、 。
。
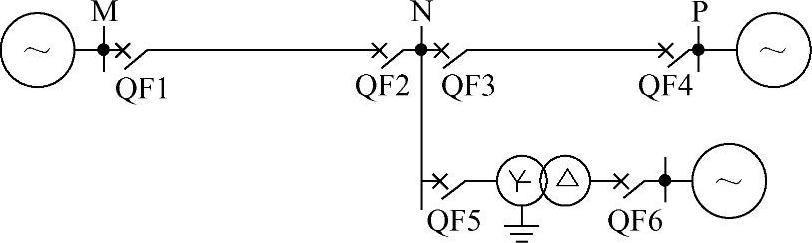
图3-40 例3-25系统接线图
分析:接地距离保护的整定计算有两个问题需要注意:
(1)接地距离保护在接线方式中采用了零序电流补偿系数 ,因此它只能反应本线路正序阻抗,而当与相邻线路接地距离保护配合时,因相邻线路的
,因此它只能反应本线路正序阻抗,而当与相邻线路接地距离保护配合时,因相邻线路的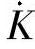 值不一定与本线路的相同,使测量阻抗发生变化。因此,在整定配合时,要考虑由于
值不一定与本线路的相同,使测量阻抗发生变化。因此,在整定配合时,要考虑由于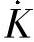 值不同而产生的影响。
值不同而产生的影响。

图3-41 接地距离保护整定配合说明图
(2)接地距离保护与相邻线路的接地距离保护相配合,不能简单地按照相间距离保护的整定原则进行计算。接地距离保护的Ⅱ、Ⅲ段整定中的正序分支系数和零序分支系数不仅大小不同,而且各自随运行方式的变化而变化,并没有固定的比例关系,使得整定变得复杂。如图3-41所示,已知线路正序阻抗等于负序阻抗,接地距离保护3的第Ⅰ段的整定阻抗为ZⅠset3。在保护3的Ⅰ段保护范围末端F点发生单相接地故障时,保护1的测量阻抗为
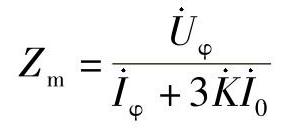
式中,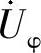 、
、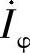 分别为保护1安装处的故障相电压和相电流。
分别为保护1安装处的故障相电压和相电流。
为了使保护1和保护3配合,则保护1第Ⅱ段的整定阻抗为
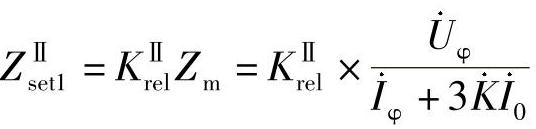
式中, 。
。
各序电压为

其中,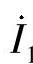 ,
, ,
,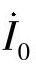 和
和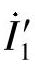 ,
,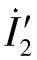 ,
,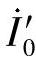 为分别流过保护1和保护3的各序电流;
为分别流过保护1和保护3的各序电流; ,
,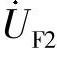 ,
, 为故障点各序电压;ZMN1,ZMN0为线路MN的正、零序阻抗;ZⅠ0set3为与距离保护3第Ⅰ段保护范围相对应的零序阻抗。
为故障点各序电压;ZMN1,ZMN0为线路MN的正、零序阻抗;ZⅠ0set3为与距离保护3第Ⅰ段保护范围相对应的零序阻抗。
根据故障分析知识,有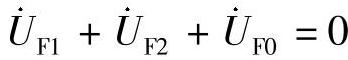 ,当各序分配系数相同时,
,当各序分配系数相同时,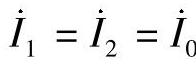 ,
,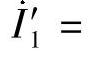
 。
。
将各序电压表达式代入测量阻抗,整理后得
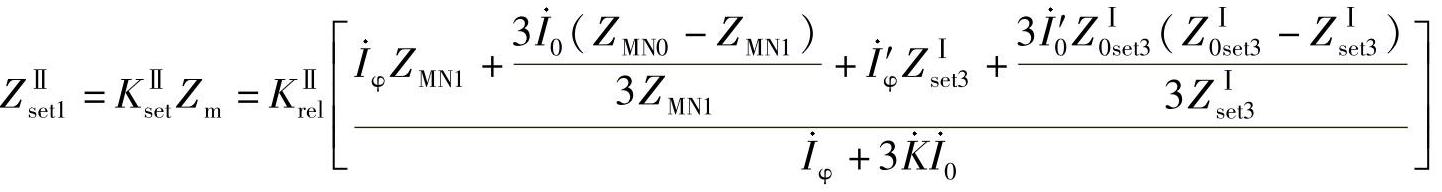
式中,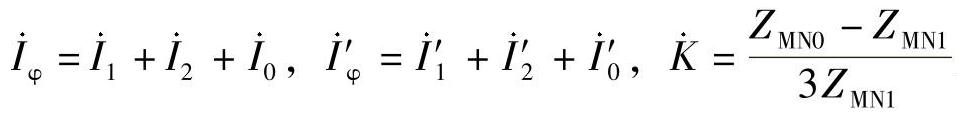 为线路MN的零序电流补偿系数;
为线路MN的零序电流补偿系数;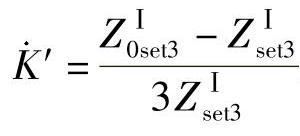 为相邻线路的零序电流补偿系数。则上式可简化为
为相邻线路的零序电流补偿系数。则上式可简化为
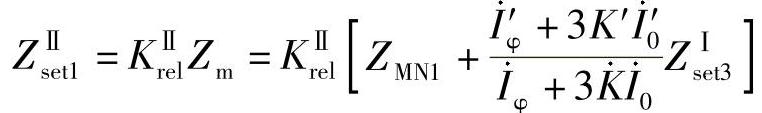
令正、负序分支系数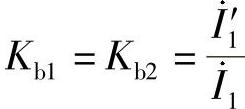 ,零序分支系数为
,零序分支系数为 ,则上可写为
,则上可写为
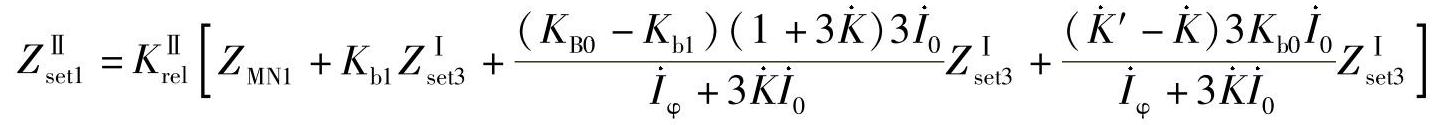
在实际整定计算中,若采用上式整定接地距离保护,将使计算十分复杂。根据DL/T 559—1994《220~500kV电网继电保护装置运行整定规程》规定,接地距离保护与相邻线路接地距离Ⅰ段配合时,ZⅡset1=KⅡrel(ZMN+KbZⅠset3),其中,Kb选用正序分支系数和零序分支系数中的较小值。
保护1第Ⅰ段的整定:
ZⅠop=0.7×28.44Ω=19.91Ω
保护1的第Ⅱ段的整定
与相邻线路配合,ZⅠset3=0.7×7.39Ω=5.55Ω
本线路补偿系数:
相邻线路补偿系数: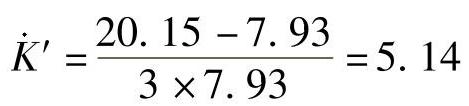
零序分支系数: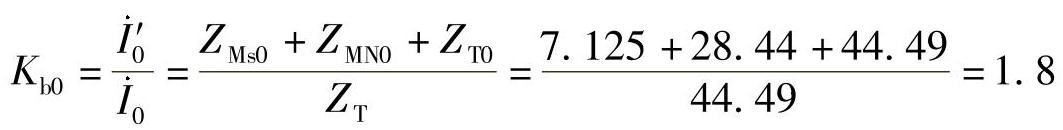
ZⅡset1=KⅡrel(ZMN1+KbZⅠset3)=0.7(11.45+1.8×5.55)Ω=15Ω
【例3-26】 表3-4给出了4次故障情况下在保护安装处测量到的三相电流突变量。试利用相电流突变量选相方法判别出故障类型和相别。
表3-4 保护安装处测量到的相电流突变量 (单位:kA)

【解】 选相元件有两个作用:
(1)选相跳闸,实现单相重合闸或综合重合闸。
(2)在故障后仅投入故障特征最明显的阻抗测量元件。
在传统模拟式保护中选相功能由选相继电器实现;数字式保护中选相功能由故障类型、故障相别的判别程序实现。数字式保护常用的选相方法有相电流差突变量选相、对称分量选相、阻抗选相、电压选相等。
相电流差突变量选相的流程如下:
1)计算三相相电流突变量幅值(①、②、③)。
2)比较①、②、③,并将它们排序(大、中、小)。
3)计算“大-中”、“中-小”。
4)若“大-中”>“中-小”,则为单相接地故障,“大”对应故障相;若“大-中”<“中-小”,则为两相故障,“小”为非故障相(利用是否有零序判断是否为接地故障);若“大-中”≈“中-小”,则为三相短路故障。
情况1:B相接地故障;情况2:BC两相接地故障;情况3:AC两相短路;情况4:三相短路。
【例3-27】 如图3-42所示,网络中M处电源电抗分别为XsM.min=20Ω,XsM.max=25Ω;N处电源电抗分别为XsN.min=25Ω,XsN.max=30Ω;电源相电动势为Es=115/3kV;线路MN最大负荷电流为350A,负荷功率因数为0.9。线路电抗为0.4Ω/km,线路阻抗角为70°。归算至电源侧的变压器电抗XT=44Ω。保护7的后备保护动作时间为1.5s,保护8的后备保护动作时间为0.5s。母线最小工作电压Uw.min=0.9UN;可靠系数分别为KⅠrel=KⅡrel=0.8,KⅢrel=0.7。若线路装有三段式相间距离保护,且测量元件为方向特性阻抗继电器,问:
(1)断路器QF1处各段阻抗保护动作阻抗为多少?整定阻抗又为多少?
(2)断路器QF1处三段距离保护灵敏度为多少?
(3)系统在最大运行方式下发生振荡时,哪些测量元件将会误启动作?为什么?
(4)距离QF112km处发生带过渡电阻RF=8Ω的相间短路故障时,该保护第Ⅱ、Ⅲ段阻抗元件是否启动?为什么?

图3-42 例3-27系统接线图
分析:当阻抗元件采用圆特性方向阻抗继电器时,短路阻抗角与整定阻抗角不相等时,动作阻抗与整定阻抗不相等;系统发生振荡时,距离保护是否会误动作取决于振荡周期、动作区及保护动作延时;短路点存在过渡电阻时,相间距离保护测量阻抗仅为过渡电阻的一半。
【解】 距离保护最大灵敏角取70°,保护Ⅰ、Ⅱ段动作阻抗与整定阻抗相等。
(1)保护1距离Ⅰ段整定值:
因为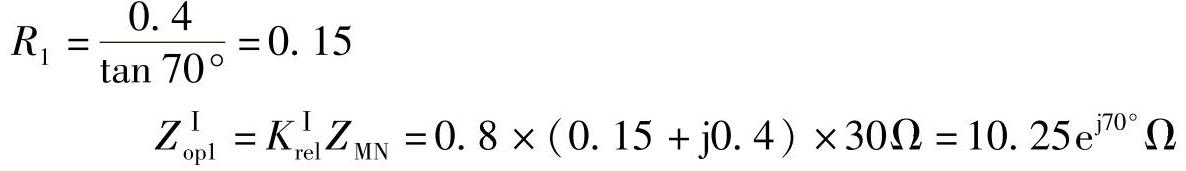
(2)保护1的距离Ⅱ段整定值。
1)与相邻线路配合:
ZⅠop2=KⅠrelZNP=0.8×0.4×60Ω=19.2Ω
分支系数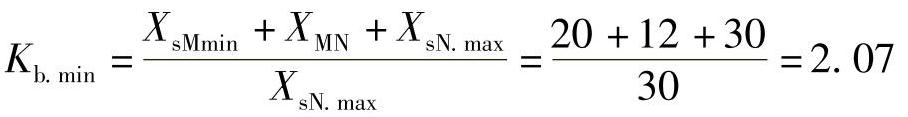
ZⅡop1=KⅡrelZMN+KⅡrelKb.minZⅠop2=0.8×(0.4×30+2.07×19.2)Ω=41.4Ω
2)与相邻变压器配合:
ZⅡop1=KⅡrelZMN+K″relKb.minZT.min=0.8×12Ω+0.7×2.07×44Ω=73.4Ω
保护整定值取41.4Ω。
3)保护灵敏度:Ksen=41.4/12=3.45
保护动作时间取0.5s。
(3)保护1的距离Ⅲ段整定值。

1)动作阻抗:ZⅢop1=KⅢrelZL.max=0.7×163.5Ω=114.5Ω
2)整定阻抗: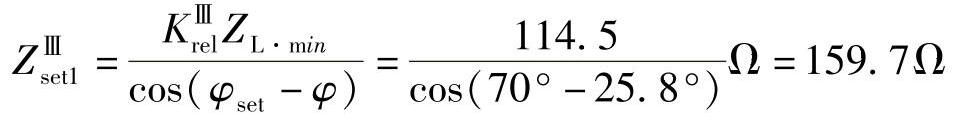
3)最大分支系数:
4)灵敏系数。
①近后备:

②远后备:
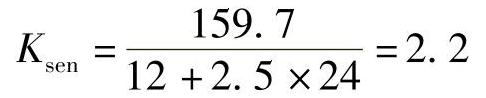
(4)系统振荡时最大电流。
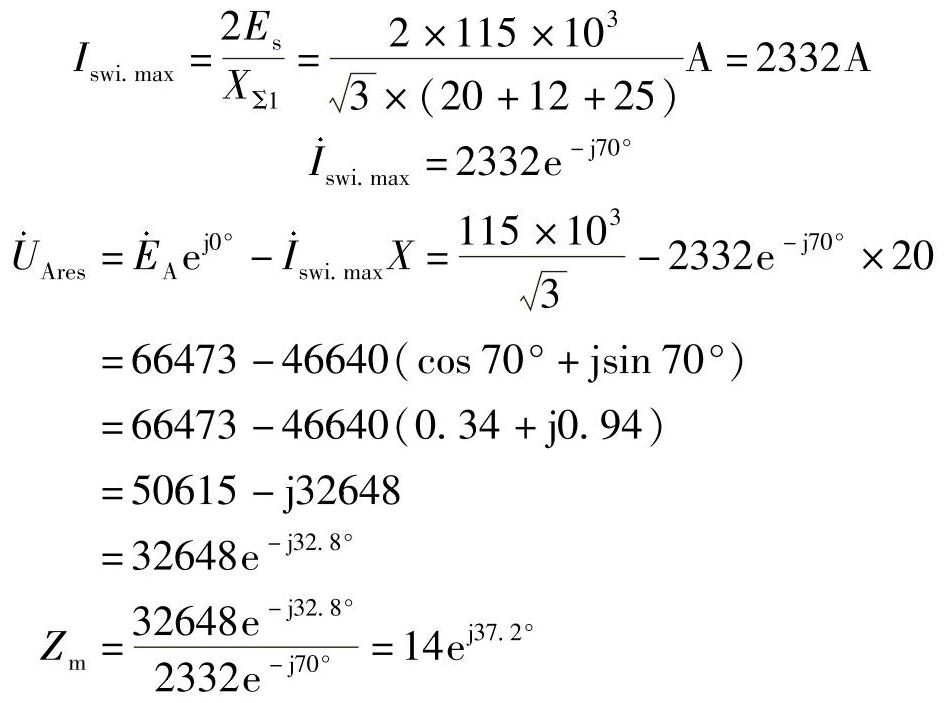
保护1的Ⅰ段动作阻抗:ZⅠop1=9.6cos(70°-37.2°)=8.06Ω
保护1的Ⅱ段动作阻抗:ZⅡop1=41.4cos(70°-37.2°)=34.8Ω
保护1的Ⅲ段动作阻抗:ZⅢop1=159.7cos(70°-37.2°)=134.2Ω
从分析可知,保护1的Ⅱ段、Ⅲ段会误启动作。
(5)经过渡电阻相间短路时:
Zm=(0.15+j0.4)×12+4=5.8+j4.8=7.5ej39.6°
ZⅡop1=41.1cos(70°-39.6°)=35.7Ω
ZⅢop1=159.7cos(70°-39.6°)=137.7Ω
保护1的经过电阻相间短路,保护1的时Ⅱ段、Ⅲ段会启动,因为测量阻抗小于动作阻抗。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




