实例：2.5微机保护算法

【例2-28】 设输入相电压、相电流分别为u（t）=U_msin（ωt+φ_u），i（t）=I_msin（ωt+φ_u-θ）；并已知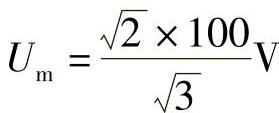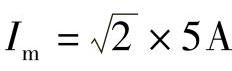，，ω=100π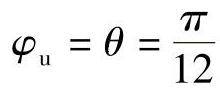，，取每周期采样次数N=12，写出一个基频周期的采样值。

【解】 因为N=12，所以每隔5/3ms采样一次。以电压为例：

第一个采样点为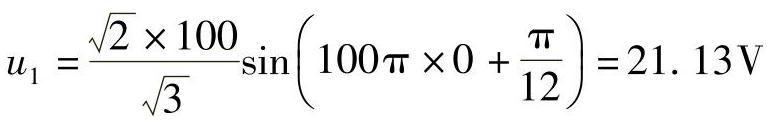

第二个采样点为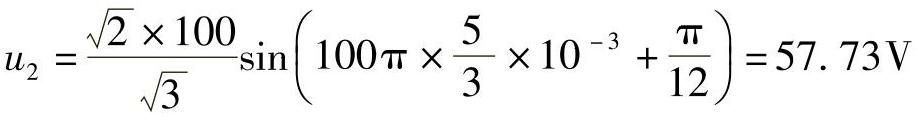

依次类推得到其他点的采样值为

【例2-29】 采用两点乘积算法，利用例2-28得到的采样序列，计算电压有效值、电流有效值、有功功率、无功功率、电阻及电抗。

【解】 假设输入量为正弦量，两点乘积法取相隔90°的采样值进行计算。当N=12时，采样周期所对应电气角度为30°，两点乘积法取相隔3个的采样值进行计算。当采样时刻发生变化时，相位也会发生变化，但是有效值不变；计算阻抗时电压量和电流量采用同时刻的采样值。

（1）取u₁=21.13，u₄=78.86；i₁=0，i₄=7.07计算：

（2）取u₂=57.73，u₅=57.73；i₂=3.54，i₅=6.12计算：

【例2-30】 利用例2-28得到的电流采样序列，采用基于正弦信号的两采样值积算法，计算电流幅值。

【解】 两采样值积算法是通过采样值之间的乘积求取信号幅值的方法。利用两采样值积算法计算电压、电流幅值的公式（以电压为例）为

式中的sin（KωT_s）、cos（KωT_s）可提前离线算出。要按最小时间延时计算，令K=1、选择KωT_s=π/2，计算量最小（计算公式与两点乘积法相同）。

（1）按最小延时计算，取i（n）=3.53，i（n+1）=6.12，即K=1，则

（2）按最小计算量计算，取i（n）=3.53，i（n+K）=6.12，即K=3，KωT_s=π／2，则I²_m=i²（n）+i²（n+K）=3.53²A+6.12²A=49.9A，。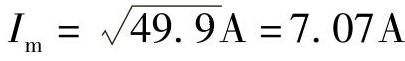

【例2-31】 利用例2-28得到的电流采样序列，采用基于正弦信号的三采样值积算法，计算电压幅值。

【解】 三采样值积算法是利用三个连续的等时间间隔的采样值，通过适当的组合求取信号幅值的方法。利用三采样值积算法计算电压幅值的公式为

式中，三个采样值之间的等时间间隔为KT_s，通常取K=1。

已知N=12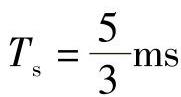，。令K=1，则sin（KωT_s）=sin30°=0.5，cos（2KωT_s）=0.5。

【例2-32】 利用例2-28得到的电流采样序列，采用基于正弦信号的两采样值算法，计算该相量的实、虚部（按最小延时和最小计算量计算）。

【解】 正弦信号u（t）=U_msin（ωt+α）对应的复相量可以表示为

U_msin（ωt+α）=U_me^jα=U_mcosα+jU_msinα=U_R+jU_Ⅰ

是一个旋转相量，通常规定逆时针为正方向，正弦信号的采样值序列可视为该旋转相量在直角复平面虚轴上的投影，如图2-39a所示。复相量的实部和虚部除了取决于幅值外，还与初相角α有关。取n作为计算起点，如图2-39b所示。n时刻u（t）在直角复平面虚轴上的投影为u（n）=U_msinα，即初相角为α时对应的虚部U_Ⅰ。n+K时刻u（t）在直角复平面虚轴上的投影为

由上式可得

图2-39 例2-32计算说明图

（1）按最小时延计算，即K=1。取u（0）=21.13和u（1）=57.73进行计算。

实部：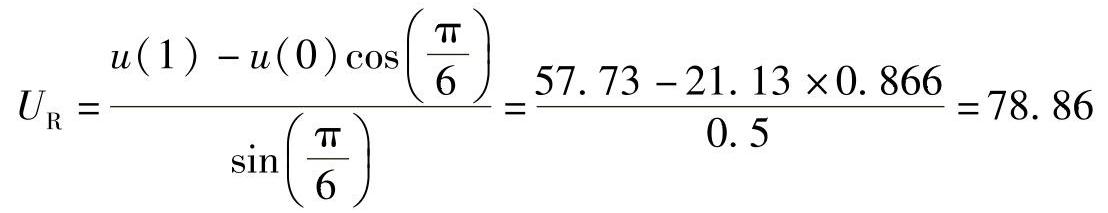

虚部：U_I=u（n）=u（0）=21.13

（2）按最小计算量计算，即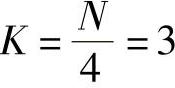。取u（0）=21.13和u（3）=78.86进行计算。

实部：U_R=u（3）=78.86

虚部：U_I=u（0）=21.13

【例2-33】 利用例2-28得到的采样序列，采用导数法计算电压有效值。

【解】 导数法也是假设输入量为正弦量。用导数法计算电压有效值需注意，利用平均值代替瞬时值、差分代替微分是会产生误差，但误差可以修正。

取u₂=57.73，u₃=78.86进行计算。

【例2-34】 图2-40所示为一周期电压信号u（t）的波形，t=0时刻对应坐标原点。已知每个周期采样12点。（1）从ωt=0时刻开始采样，利用傅里叶算法求a₁、b₁、θ₁及电压信号有效值；（2）从ωt=2π/3时刻开始采样，利用傅里叶算法求a₁、b₁、θ₁及电压信号有效值。

【解】 在微机处理时，基波分量的正、余弦项的振幅a₁、b1可用下式求得。

图2-40 三角波形图(https://www.xing528.com)

当采样时刻发生变化时，a₁、b₁、θ₁均发生变化，但有效值不变。

（1）由图可得采样值：u₀=0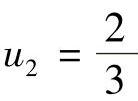，，，u₃=1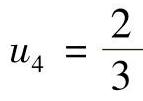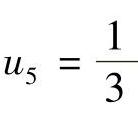，，，u₆=0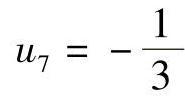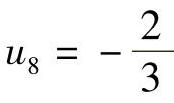，，，u₉=-1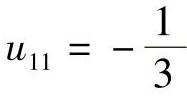，，，u₁₂=0。

将上述采样值代入傅里叶算法，得

（2）采样值为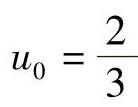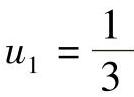：，，u₂=0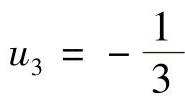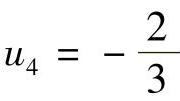，，，u₅=-1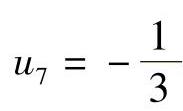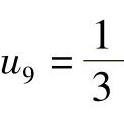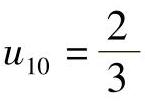，，，，，，u₁₁=1，。

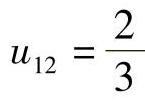将采样值代入傅里叶算法，得，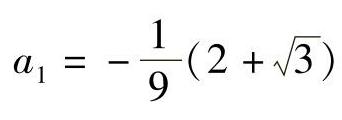

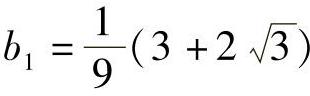
【例2-35】 采样序列为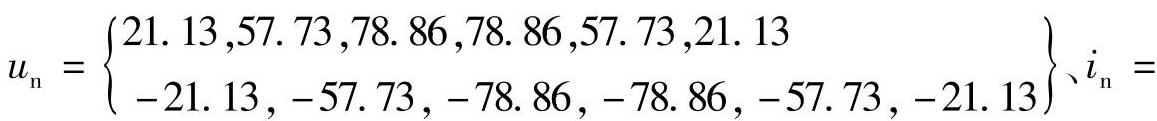，采用解微分方程算法，计算电阻及电抗。

【解】 解微分方程算法也称为R-L模型算法，仅用于计算线路阻抗。通过滤除短路后产生的高频分量，将输电线路等效为R-L模型，如图2-41所示。

根据R-L模型，短路时下式成立。

上式中，u、i和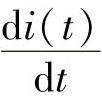都是可以测量或计算得到的，未知数有R₁、L₁。采用两个不同时刻t₁和t₂分别测量或计算u、i和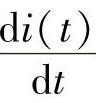，就可以得到两个独立的方程为

图2-41 R-L模型图

式中，。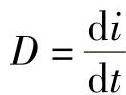

求解独立方程式，即可得到R₁、L₁。利用上式求解时需要注意（k为自然数）。

解微分方程算法还有下面两种形式。

1）

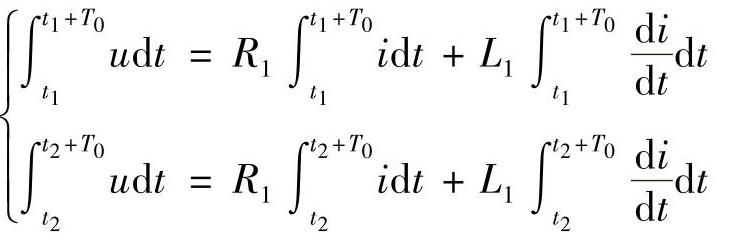
2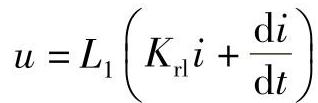），其中K_rl=R₁/L₁为已知。

本例用独立方程式求解。选择n=0、n=1、n=2三个时刻的采样值，则

将u₁、u₂、i₁、i₂、D₁、D₂代入方程式得

求得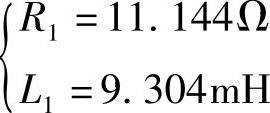

【例2-36】 已知采样频率f_s=600Hz，设采样序列u（n）、i（n）已经过数字滤波，只含基波分量，微机保护中方向元件的动作方程为u（2）i（1）+u（5）i（4）≥0，画出该方向元件的动作特性（以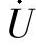为基准相量）。

【解】 本例涉及移相算法和相位比较算法。在实现继电保护原理时，常常要求相量旋转一个相位角（或改变一个正弦函数的初始相位），并保持其幅值不变，称移相算法。

改变一个正弦量输入信号的初始相位最简单的方法是时差法。设输入信号为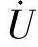，对应的正弦信号为u（t）=U_msinωt；将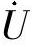逆时针方向移相α=ωΔt，即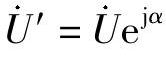，对应的正弦信号为u′（t）=u（t+Δt）=U_msin（ωt+α）。

对于离散采样值序列，只有在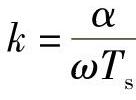为整数时才能利用时差法进行准确移相。

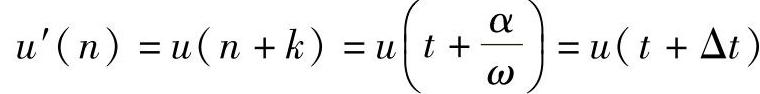，其中Δt=kT_s。滞后kT_s采样得到的u′（n）对应的相量超前u（n）所对应相量。

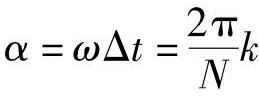相位比较算法包含余弦型和正弦型两类。本例属于余弦型。余弦型相位比较的表达式为

令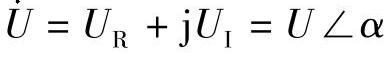，则U_R=Ucosα，U_I=Usinα；，则I_R=Icosβ，I_I=Isinβ。

上式可表示为-90°≤（α-β）≤90°。即cos（α-β）≥0；展开得cosαcosβ+sinαsinβ≥0。公式两边同乘以UI，则UIcosαcosβ+UIsinαsinβ≥0，即

（Ucosα）（Icosβ）+（Usinα）（Isinβ）≥0

进一步可表示为

U_RI_R+U_ⅠI_Ⅰ≥0

由于f_s=600Hz，则ωT_s=30°。u（5）=u（2+3）=u（2T_s+3T_s）=u（2ωT_s+90°），i（4）=i（1+3）=i（ωT_s+90°）。

图2-42 方向元件动作特性图

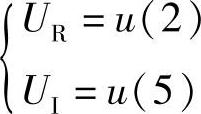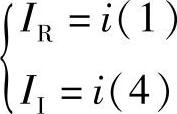、，由u（2）i（1）+u（5）i（4）≥0，可得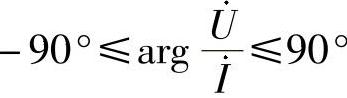，其中。方向元件的动作特性如图2-42所示。

【例2-37】 已知采样频率f_s=600Hz，试分析由式u（n）=［u_a（n）+u_b（n-4）+u_c（n+4）］计算得到的u（n）是正序还是负序分量。

【解】 已知f_s=600Hz，则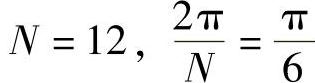。根据移相算法，u_a（n）对应的相量为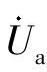；u_b（n-4）对应的相量为；。

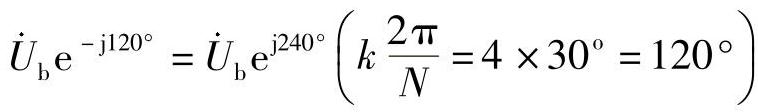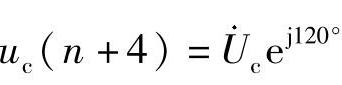根据对称分量法，，因此u（n）是负序分量。