简易法展开例136圆管三节90°弯头

已知圆管直径φ为40，圆管弯头中心弧线R为50，节数N为3，角度α为90°，求做展开。

展开步骤：

1）根据已知条件求做中心弧线切线的总长（即圆管用料总长，见图2-221）求做步骤为：①做一90°角，以顶点O为圆心，50为半径画弧，弧线交直角两边上的点为1点和5点。②等分所得弧线，等分数为（N-1）×2=（3-1）×2=4，即弧线被四等分，等分点为1、2、3、4、5点。逢单数点做切线与中心圆弧线相切，相邻两切线相交，得交点为O₁点和O₂点，那么1点至O₁点、O₁点至O₂点、O₂点至5点的切线长之和即为切线总长，也就是圆管用料的总长。在中心弧线被分成四等分的同时，90°角也被分成四等分，每等分的角度为22.5°。

2）在适宜位置做圆管底边线段AB，线段AB的长等于圆管的直径。过线段AB中点向上做垂线，垂线长等于1点至O₁点、O₁点至O₂点、O₂点至5点的总长。以5点为中点的做平行于线段AB的线段CD，线段CD长等于圆管直径。用线段连接A点至C点、B点至D点，所得矩形ABCD就是圆管90°三节弯头用料长度的投影图。

3）过圆管用料长度投影图中的O₁点、O₂点做线段AB的平行线。做两条切割线分别过O₁点和O₂点，切割线与O₁点和O₂点平行线的夹角为22.5°。两条切割线分别与圆管两条边AC与BD相交，在AC上得交点M、K，在BD上得交点N、H。那么线段MN和KH就是圆管90°三节弯头的相贯线。在圆管底边线段AB上做圆管的半圆，并把半圆六等分，等分点为1、2、3、4、5、6、7点。过这七个等分点向上做线段CD的垂线，七条垂线分别经过切割线（即相贯线）MN和KH，在相贯线MN和KH上得交点同为1、2、3、4、5、6、7点。(www.xing528.com)

4）做线段AB、CD向右引的延长线，并过两条切割线上的各交点做线段AB延长线的平行线。在线段AB、CD的延长线上对应截取长等于圆管周长的线段。十二等分线段AB的延长线段，过各等分点做延长线的垂线，十三条垂线与两条切割线上各交点引过来的平行线对应相交，得各对应交点同为1、2、3、4、5、6、7、6、5、4、3、2、1点。用曲线圆滑连接这些点，即得到圆管90°三节弯头相贯线的展开，整个矩形即为圆管90°三节弯头的展开图。

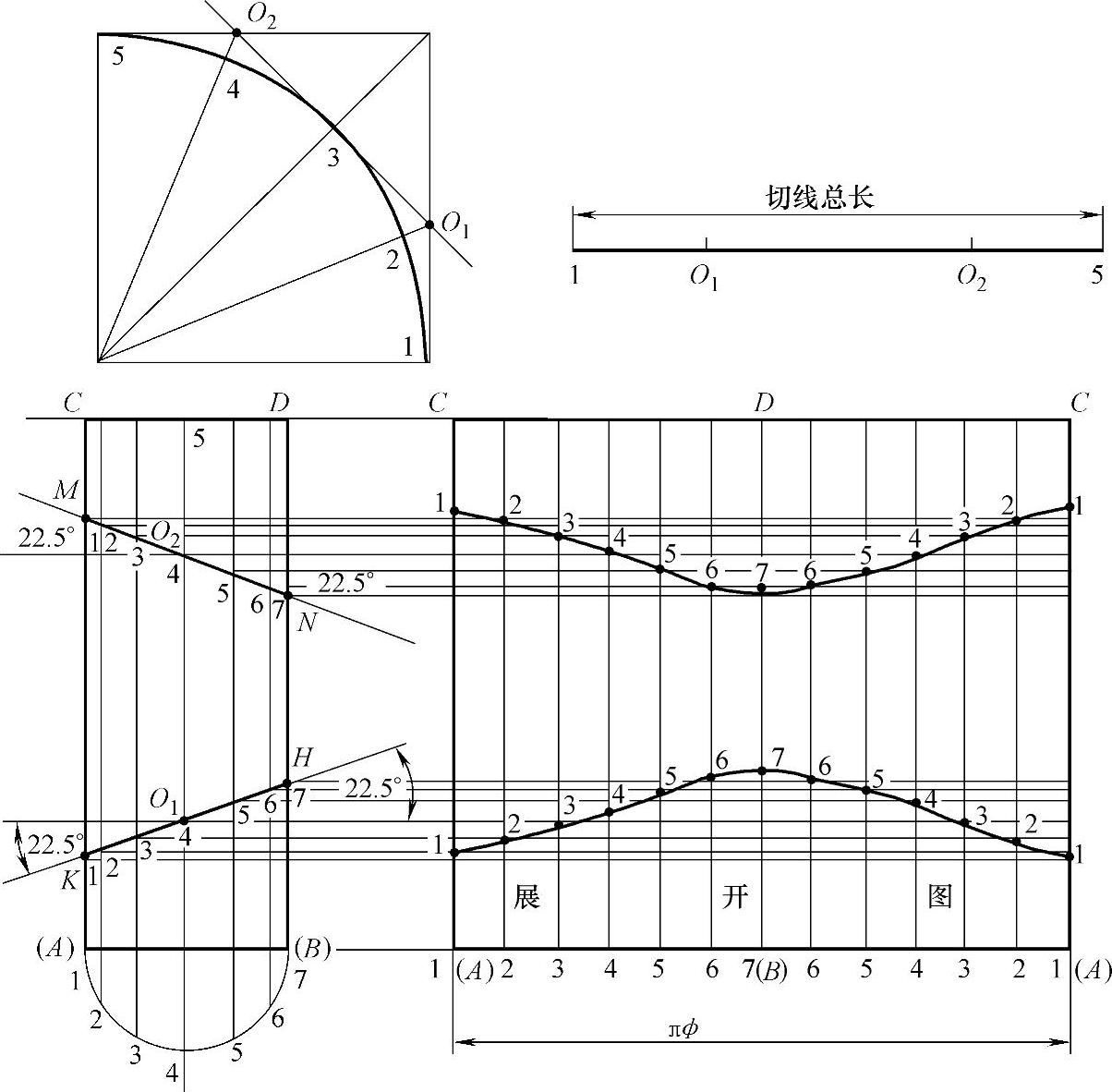
图2-221 圆管90°三节弯头的展开图