轻松计算地方体展开的例130天圆法

为了说明应用计算方法做天圆地方体展开的过程，先做天圆地方体的主、俯两视图，并把主视图上各端点标为A、E、B、D、F、C点，俯视图上各端点标为A′、F′、E′、B′、G′、H′点，线段EF为天圆地方体的高（见图2-213）。

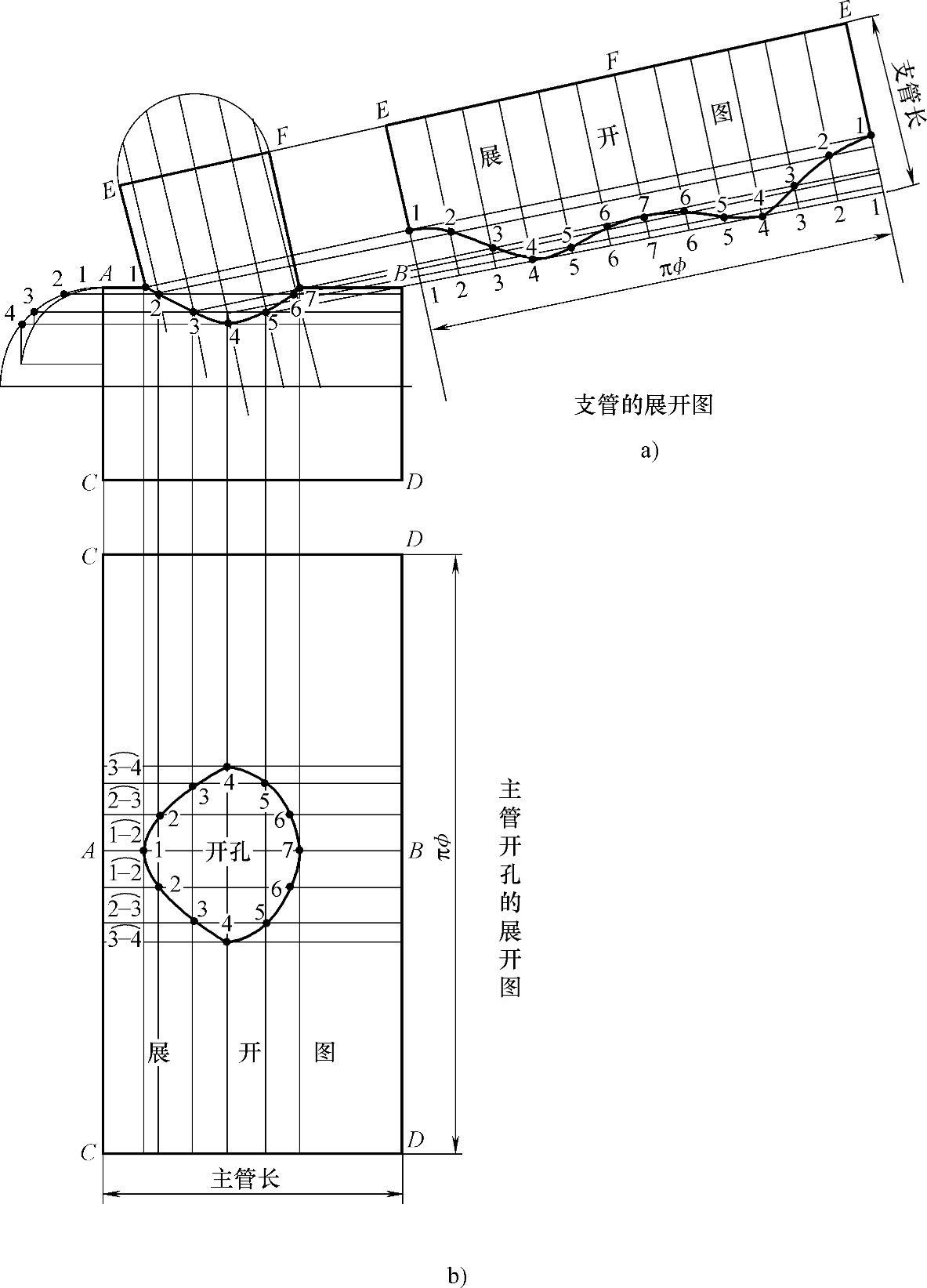
图2-212 异径圆管斜交三通管的展开图

a）支管的展开图 b）主管开孔的展开图

应用计算法的步骤：用直角三角形做图法求做天圆地方体一侧面板中线的实长线，即用地方体底线段AB的长减去天圆直径长φ，再除以2，所得定为直角三角形一直角边EN即EN=（AB-φ）/2，线段EF为直角三角形另一直角边。做两条直角边端点F点至N点的连线，即直角三角形的斜边长，此斜边长即为所求天圆地方体一侧面板中线的实长线。应用勾股定理可求出实长线，直角三角形底边为EN，直角三角形直角边高为EF，直角三角形斜边为FN，FN即为所求实长线。

计算公式：

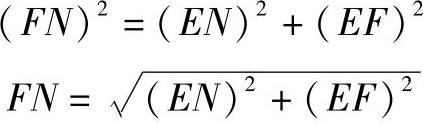
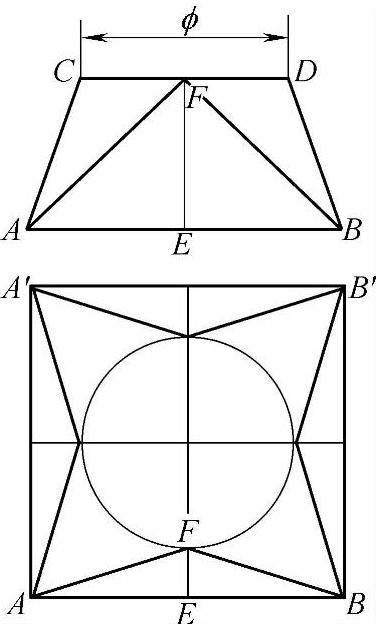
图2-213 天圆地方体示意图

天圆地方体的展开图：在一适宜地方做天圆地方体的地方底线段AB，线段AB中点为E点，过E点向上做垂线段EF′垂直于线段AB，线段EF′为天圆地方体一侧面板中线的实长线。以F′点为圆心，天圆1/4圆周长为半径画圆，再分别以线段两端点A点和B点为圆心，以A点至F点长为半径画弧，两弧相交于圆周线上，得到两个交点分别为M₁、M₂点。分别以M₁、M₂点和F′点为圆心，以大于M₁点至F′点的1/2线段长为半径画弧线，两弧相交得到交点1、2、3和4。用直线连接1点至2点和3点至4点，两条直线的交点为O点则O点即为所求天圆地方体展开时的圆心。以O点为圆心，O点至F′点线段长为半径画弧，弧线同时经过M₁、M₂点和F′点。分别以M₁、M₂点为圆心，M₁点至F′点线段长为半径画弧，与上一步所画弧线上相交，得交点为M′、M″。以O点为圆心，O点至A点线段长为半径画圆，线段AB的两端点A点和B点分别在此圆周线上。分别以A点和B点为圆心，线段AB长为半径画弧，与上一步所画圆相交，得交点为H′点和G点。以G点为圆心，线段AB长为半径画弧，与前所画的圆相交，得交点为A″点。用线段把地方底A点与天圆圆周线上的M′点和M₁点分别相连。用线段把地方底A点与天圆圆周线上的M₁点和F′点分别相连。用线段把地方底B点与天圆圆周线上的F′点和M2点分别相连。用线段把地方底的B′点与天圆圆周线上的M₂点和M″点分别相连。用线段把地方底的A″点与天圆圆周线上的M″点相连。用线段把地方底A′点至A点、B点至B′点、B′点至A″点分别相连。相连后的图形即为天圆地方体的展开图。

[计算法求做天圆地方体展开的应用举例]

已知天圆地方体商EF为40，地方底宽为80，天圆直径为40（见图2-214），求做展开。

1）求做天圆地方体一侧面板中线的实长线：用直角三角形做图法求做实长线。(www.xing528.com)

用地方底线段AB减去天圆直径φ，再除以2，得EN，EN即为直角三角形的一条直角边。

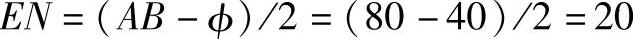
天圆地方体主视图的高（即EF）为直角三角形另一直角边，已知天圆地方体高为40，那么EF=40。

做两条直角边端点F点至N点的连线，所得直角三角形的斜边长就是所求的一侧面板中线的实长线（见图2-214a）。

2）计算法求实长线：应用直角三角形勾股定理，即a²+b²=c²（式中a和b代表三角形的两条直角边，c代表直角三角形的斜边）。

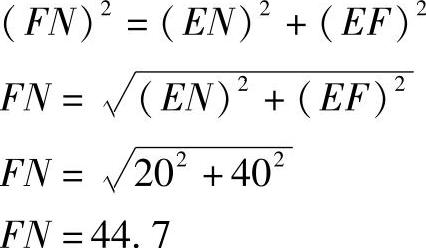
3）做天圆地方体的地方线段AB=80，做线段AB的中点E，过E点向上做垂线段EF′垂直于线段AB，EF′=44.7（即天圆地方体一侧面板中线的实长线）。

4）求做天圆地方体展开时的圆心点：以F′点为圆心，天圆的1/4圆周线（即3/4）长为半径画圆；再分别以地方底线段AB两端的A点和B点为圆心，A点至F′点长为半径画弧，两弧线相交于圆周线上，得到两个交点M₁和M₂。分别以M₁、M₂和F′三点为圆心，以大于M₁点至F′点线段长为半径画弧，弧线与弧线相交，得交点为1、2、3、4点。用直线连接1点至2点和3点至4点，两条直线交于点O，O点即为所求天圆地方展开时的圆心。

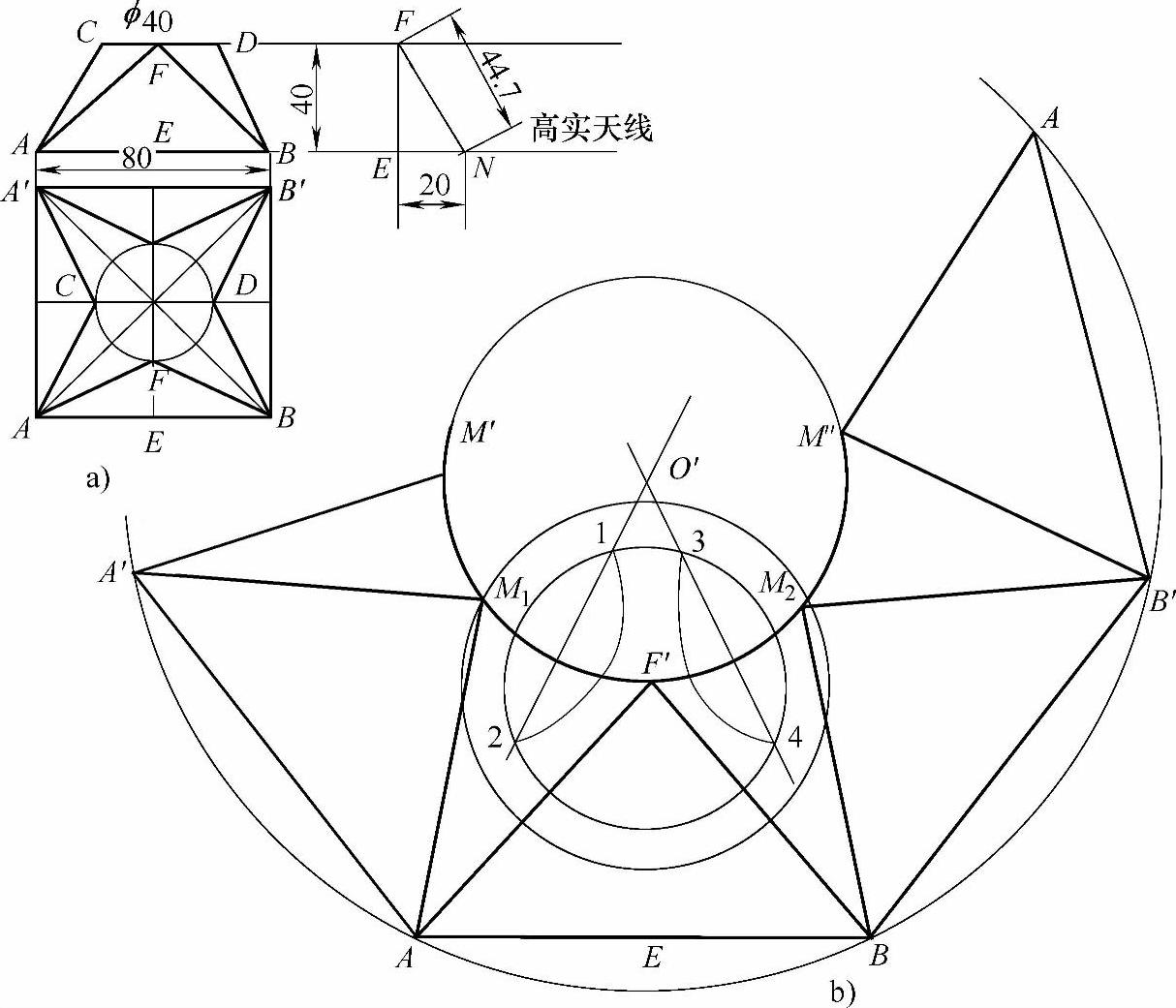
图2-214 用计算方法做的天圆地方体的展开图

a）主、俯视图及高的实长线 b）计算法做出的展开图

5）做天圆地方体的展开图：以O点为圆心，O点至F′点的线段长为半径画弧，弧线同时经过M₁、M₂和F′点。分别以M₁、M₂点为圆心，M₁点至F′点线段长为半径画弧，在上步所画弧线上得两个交点M′和M″。以O点为圆心，O点至A点线段长为半径画圆，线段AB的端点A和B分别在此圆上。分别以A点和B点为圆心，线段AB长为半径画弧，与上步所画圆相交；得交点为A′点和B′点。以B′点为圆心，线段AB长为半径画弧，与前面所画圆相交，得交点为A″点。用线段把地方底A′点与天圆圆周线上的M′点和M₁点分别相连。用线段把地方底的A点与天圆圆周线上的M₁点和F′点分别相连。用线段把地方底的B点与天圆圆周线上的F′点和M₂点分别相连。用线段把地方底的B′点与天圆圆周线上M₂点和M″点分别相连。用线段把地方底的A″点与天圆圆周线上M″点相连。用线段把地方底的A′点至A点、A点至B点、B点至B′点、B点至A″点分别相连。相连后的图形即为高40、天圆直径40、地方底长80的天圆地方体的展开图（见图2-214b）。