展开例116方管水平偏交圆锥管

1）根据已知条件做出方管水平偏交圆锥管的主、俯两视图，并做方管的断面图（见图2-199）。

2）求做两管相交的相贯线：从主、俯两视图中看到，主、俯两视图都不存在相贯线，两管又不存在两管轴心线的共交点，因此只能用截平面法去求做相贯线。利用现有已知条件，首先做出俯视图中的相贯线，而后由俯视图中的相贯线上的相贯点向上往主视图引垂线，以点对线找出主视图中的相贯点，再由若干个相贯点相连而组成主视图中的相贯线。

俯视图中相贯线的求做过程：在主视图方管断面图中做棱线BA向右的延长线，为切割线1。再做棱线DC向右的延长线，为切割线5，两条切割线交在圆锥管两边线OE和OF上得交点分别为1点和5点。在俯视图中以圆锥管锥顶O点为圆心，主视图中圆锥管两边线间的切割线（即1-1和5-5）的1/2长为半径分别画弧，弧线经过方管上下两条棱线的延长线，其中：以1点切割线的1/2为半径所画弧线过方管棱线A′和B′，在A′棱线上得交点为A′点，在B′棱线上得交点为B′点，以5点的切割线的1/2为半径所画弧线过方管棱线C′和D′，在C′棱线上得交点为C′点，在D′棱线上得交点为D′点。那么A′、C′、D′、B′四点所围成的图形就是两管相交在俯视图中的相贯线。

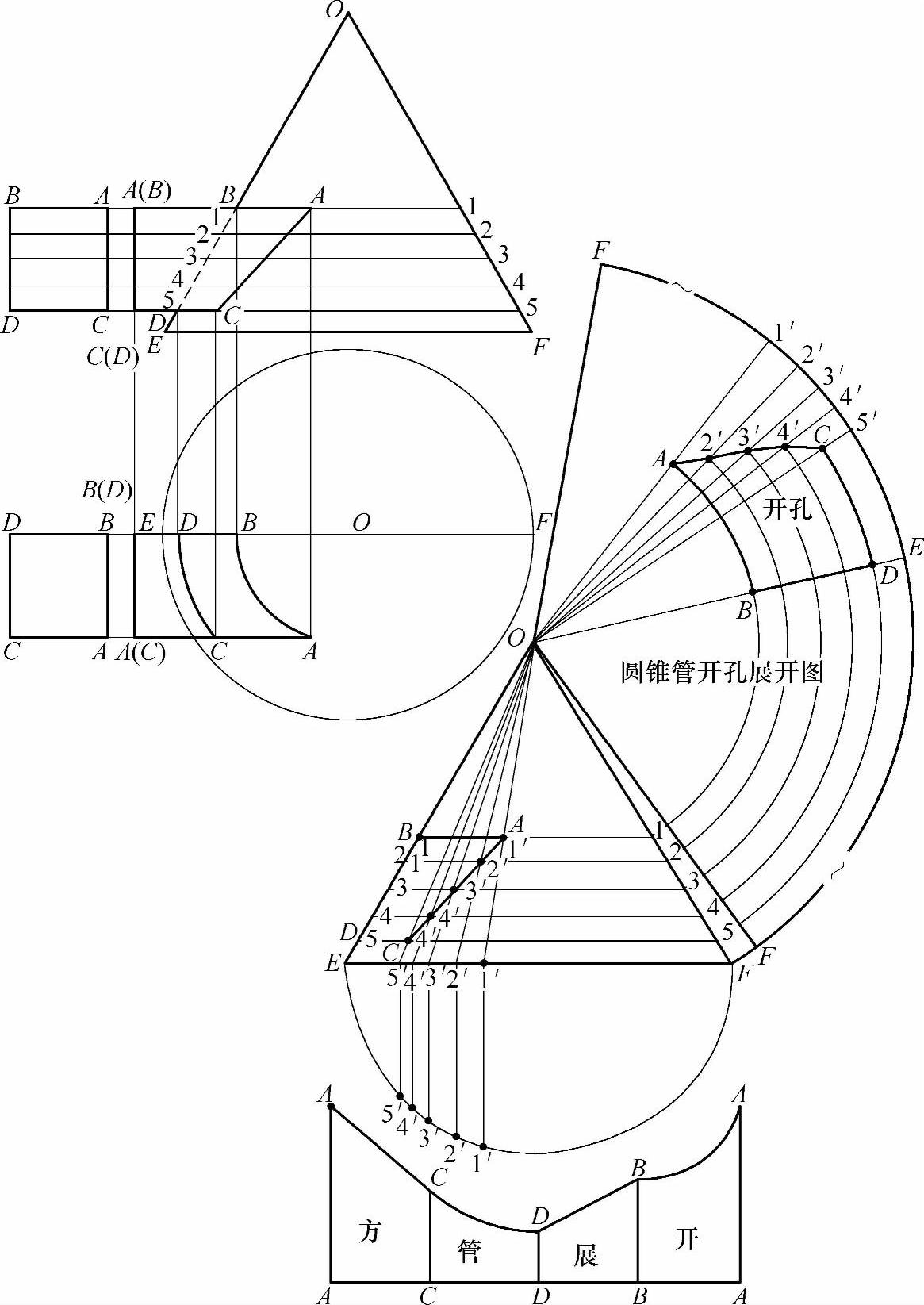
图2-199 方管水平偏交圆锥管的展开图

主视图中相贯线求做过程：过俯视图相贯线上的四个相贯点A′、B′、D′、C′向上往主视图引垂线垂直于主视图锥底线段EF。垂线过锥底线段EF，交于主视图中方管两条棱线的延长线上，即1切割线1-1、5-5上，在切割线1-1上得交点为B点和A点，在切割线5-5上得交点为D点和C点。从前小节“相贯线的性质与特点”中知道：方管与圆锥管相交的相贯线为直线，所以分别用线段连接两条切割线上的交点，即切割线1-1上B点至A点及切割线5-5上的D点至C点。切割线1-1上的B点至切割线5-5上的D点，因为是看不见的，所以用虚线相连。切割线1-1上的A点至切割线5-5上的C点用线段相连。那么相连的ABDC封闭图形即为所求主视图中的相贯线。

3）展开。

方管的展开：做一水平线，在水平线上任选一点为A点，以A点为起点，主视图左前端方管断面图中的四条棱线AC、CD、DB、BA为半径依次画弧截取这条水平线，在水平线得交点为A、C、D、B、A点。过水平线上这些交点做上垂线垂直于水平线。分别量取这些垂线长，A点的垂线长等于主视图A（B）点至A点长，C点的垂线长等于主视图C（D）点至C点长，D点的垂线长等于主视图C（D）点至D点长，B点的垂线长等于主视图A（B）点至B点长。分别用线段连接A点至C点和D点至B点。分别用曲线连接C点至D点和B点至A点，相连的这两条曲线即是俯视图中相贯弧线和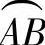的实际曲线，那么相连后的图形即为方管的展开。

圆锥管的展开：从前述“相贯线与展开线关系”中得知，圆锥管的相贯线段AC不在素线上，且在做展开时是曲线。为使圆锥管相贯线段AC展开线做得准确，有必要对这段相贯线进行等分，并分段做曲线，最后把分段的曲线圆滑连接。把带有相贯线的圆锥管视图，移到一个适宜位置，以待展开。在圆锥管锥底线段EF上做锥底的半圆。具体做法如下：做圆锥管相贯线段AC的四等分（等分越多越精确），等分点为1′、2′、3′、4′、5′点。过相贯线段AC上的1′、2′、3′、4′、5′点做平行线平行于锥底线段EF，五条平行线交于圆锥管边线OF上，在边线OF上得交点为1、2、3、4、5点，那么从锥顶O点至边线OF上五个交点的长即是各相贯点素线实长。从锥顶O点引素线分别过相贯线段AC上的五个等分点，交于锥底线段EF上，得交点为1′、2′、3′、4′、5′点。过锥底线段EF上的1′、2′、3′、4′、5′点做垂线垂直于锥底线段EF，交于锥底所画的半圆周线上，在锥底半圆周线上得交点依次为1′、2′、3′、4′、5′点，那么锥底半圆周线上的这些交点就是各自相贯点素线至锥底圆周线上相交的实际位置点。

方管与圆锥管相交的开孔展开步骤：以锥顶O点为圆心，锥顶O点至锥底端点F的素线长为半径画弧，在这条弧线上任选一点为F点，以F点为起点，以锥底半圆六等分中的一份弧长为半径，依次截取弧线十二次，得终点为F点（弧线长即圆锥管底圆的周长）。过弧线上的起点和终点（即两个F点），分别做线段与锥顶O点相连。在圆锥管底圆周长弧线1/2处做一E点，以E点为圆心锥底半圆周线上、、、、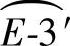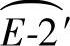的弧长为半径分别画弧，依次截取圆锥管底圆周长线，在圆锥管底圆周长线上得交点依次为5′、4′、3′、2′、1′点。过锥底圆周线上的这些交点引素线与锥顶O点相连，其中：相贯线BD线段与E点的素线重合，相贯点C点素线与5′点素线垂合，相贯线A点的素线与1′点素线重合。以锥顶O点为圆心，锥顶O点至圆锥管边线OF上的相贯点1、2、3、4、5点各素线实长为半径分别画弧，各弧线与锥底圆周线上所引各条素线分别对应相交，得交点为B、A（即1′点）、2′、3′、4′、C（即5′点）、D点。在视图中相贯线线段BD在同一条素线上，所以展开线为直线（见前小节，“相贯线的性质与特点”），B点至A点用同一条圆弧线相连，D点至C点，用同一条圆弧线相连。用曲线圆滑连接A′、2′、3′、4′、C点，连接后的封闭图形即是方管与圆锥管相交的开孔展开，整个图形即是圆锥管开孔的展开图。例117 方管倾斜偏交圆锥管的展开

1）根据已知条件做出方管倾斜偏交圆锥管的主、俯两视图，并在圆锥管锥底两端标注A点和B点，锥顶标注为O点。方管左前端做出方管的断面图，断面的四端点标注为E、F、M、N点（见图2_-200）。(www.xing528.com)

2）求做主视图两管相交的相贯线：从主、俯两视图中看到，两视图都不存在相贯线，两管轴线又不在一个相交点上，所以不适用素线法和球面法求做相贯线，因此只能用截平面法去求做相贯线。利用现有的已知条件，首先做出俯视图中的相贯线，然后利用俯视图中相贯线上的相贯点向上往主视图引垂线，并以点对线（即主视图上的切割线）找出主视图中的相贯点，找出几个相贯点，再用线段或曲线圆滑连接即得主视图中的相贯线。因为在第二节“相贯线的性质与特点”中得知：方管与圆锥管相交，相贯线在主视图中是直线，所以主视图中的相贯线只需找出两个相贯点，即起点和终点。两个相贯点之间用线段相连，就是主视图中的相贯线。

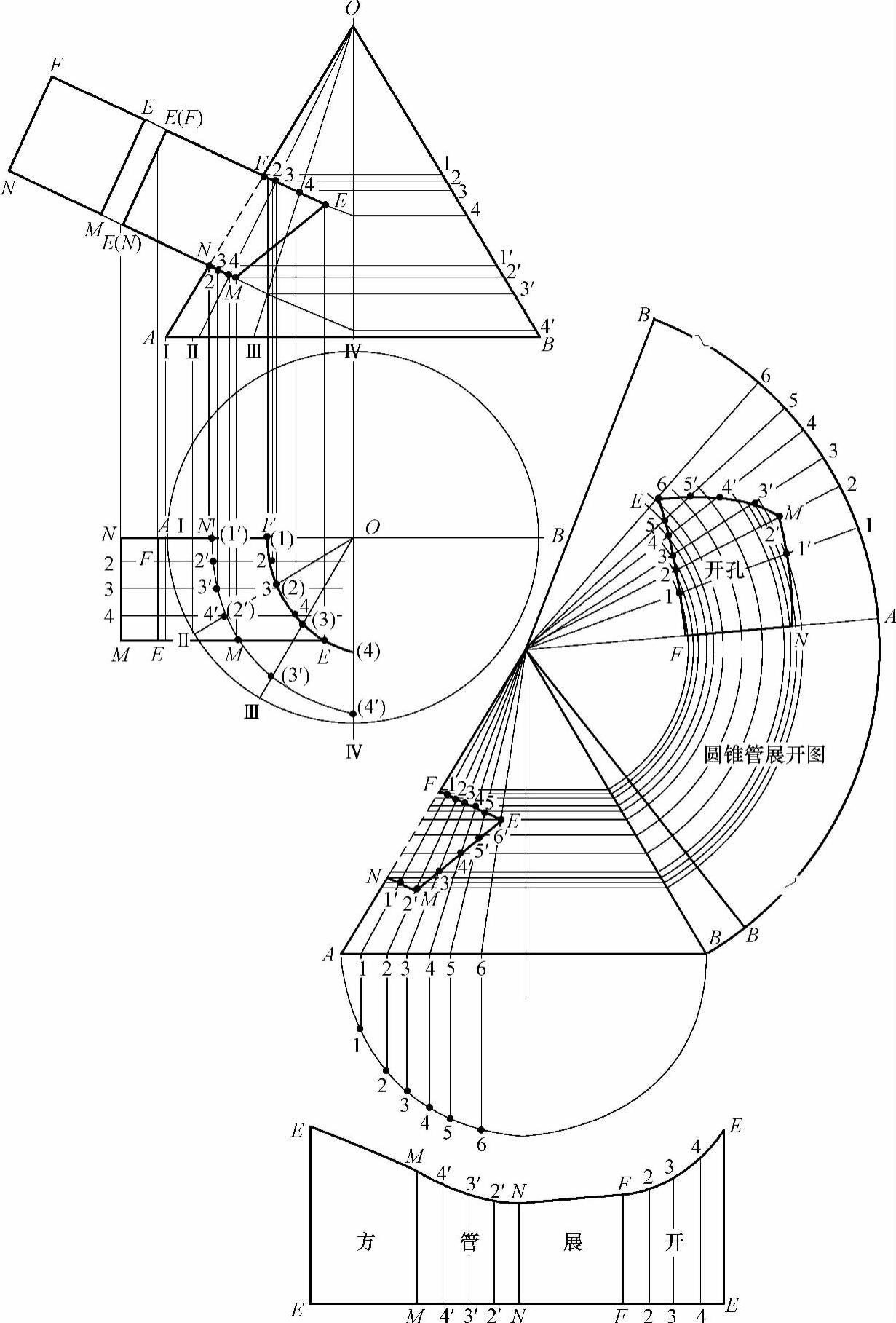
图2-200 方管倾斜偏交圆锥管的展开图

俯视图中相贯线求做过程：因为方管与圆锥管倾斜偏交，所以利用水平截平面求做相贯线是不可能完成的，因此只能用斜切截平面方法求做相贯线。斜切截平面求做相贯线方法在前面章节中已有论述，即斜切截平面，圆锥管投影是一个近似圆，支管投影为两条边夹一个面，两条边与近似圆相交，相交点即是相贯点。在俯视图中做锥底1/4圆周线的三等分，等分点为Ⅰ、Ⅱ、Ⅲ、Ⅳ点。过锥底1/4圆周线上的交点Ⅰ、Ⅱ、Ⅲ、Ⅳ点引素线与俯视图中的锥顶O点相连，得素线O-Ⅰ、O-Ⅱ、O-Ⅲ、O-Ⅳ四条。过俯视图锥底1/4圆周线上的等分点，（即Ⅰ、Ⅱ、Ⅲ、Ⅳ点）向上往主视图引垂线垂直于主视图锥底线段AB，四条上垂线交于主视图锥底线段AB上，得交点为Ⅰ、Ⅱ、Ⅲ、Ⅳ点。过主视图锥底线段上的Ⅰ、Ⅱ、Ⅲ、Ⅳ点做素线与主视图锥顶O点相连，在主视图上得素线O-Ⅰ、O-Ⅱ、O-Ⅲ、O_-Ⅳ四条。主视图方管上下棱线的延长线（也是两条切割线）分别过主视图上的四条素线，上棱线的延长线（即第一切割线），在素线O_-Ⅰ上得交点为1点，在素线O-Ⅱ上得交点为2点，在素线O-Ⅲ上得交点为3点，在素线O-Ⅳ上得交点为4点。下面棱线重叠线（MN）线延长线即第二条切割线，在素线O-Ⅰ上得交点为1′点，在素线O_-Ⅱ上得交点为2′点。在素线O-Ⅲ上得交点为3′点，在素线O-Ⅳ上得交点为4′点。过主视图素线上的交点1、2、3、4点和1′、2′、3′、4′点做平行线，平行于锥底线段AB，交于圆锥管边线OB上，在边线OB上得交点依次为1、2、3、4点和1′、2′、3′、4′点。在俯视图中以O点为圆心，主视图圆锥管边线OB上各个交点至素线O-Ⅳ交点间的平行线段长为半径分别画弧，其中：以1点平行线段长为半径所画弧线交于俯视图素线O-Ⅰ上，得交点为（1）点；以2点平行线段长为半径所画弧线交于俯视图素线O-Ⅱ上，得交点为（2）点；以3点平行线段长为半径所画弧线交于俯视图素线O-Ⅲ上，得交点为（3）点；以4点平行线段长为半径所画弧线交于俯视图素线O-Ⅳ上，得交点为（4）点；以1′点平行线段长为半径所画弧线交于俯视图素线O-Ⅰ上，得交点为（1′）点；以2′点平行线段长为半径所画弧线交于俯视图素线O-Ⅱ上，得交点为（2′）点；以3′点平行线段长为半径所画弧线交于俯视图素线O-Ⅲ上，得交点为（3′）点；以4′点平行线段长为半径所画弧线交于俯视图素线O-Ⅳ上，得交点为（4′）点。分别用曲线圆滑连接俯视图四条素线上的交点，连接后这两条曲线即是俯视图中圆锥管被斜切截面近似圆的1/4投影曲线。俯视图中方管棱线NF和ME的延长线交于两条曲线上，其中：棱线重叠（FN）线延长线交于第一条曲线上得交点为F点，交于第二条曲线上得交点为N点；棱线重叠（EM）线延长线，交于第一条曲线上得交点为E点，交于第二条曲线上得交点为M点。那么EFNM所围成的图形边即为俯视图中的相贯线。

主视图中相贯线求做过程：过俯视图中相贯线上的E、F、N和M点向上往主视图引上垂线垂直于主视图锥底线段AB，垂线与主视图方管上、下棱线的延长线相交在上棱线的延长线上得交点为E点和F点，在下棱线的延长线上得交点为M点和N点。分别用线段相接E点至M点和F点至N点，相连后的封闭图形边即为所求主视图中的相贯线。

3）展开

方管的展开：为了使方管与圆锥管相交的相贯线展开曲线做得准确，有必要对俯视图中相贯线进行约等分，按等分点进行分段，用曲线圆滑连接各分段点。相贯线约等分分段方法是把俯视图中方管左前端线段MN进行四等分，在线段MN上得交点为2、3、4点。过线段MN上交点2、3、4点做平行线平行于锥底直径线段AB，平行线过俯视图相贯曲线和，在相贯曲线上得交点为2′、3′、4′点，在相贯线曲线上得交点为2、3、4点。过俯视图相贯线上的交点2′、3′、4′点和2、3、4点向上往主视图引垂线垂直于主视图锥底线段AB，其中：2′、3′、4′点的上垂线交于主视图相贯线线段MN上，在相贯线线段MN上得交点为2′、3′和4′点；2、3、4点的上垂线交于主视图相贯线线段EF上，在相贯线线段EF上得交点为2、3和4点。做一水平线，在水平线上任选一点为E点，以这个E点为起点，主视图左前端方管断面图中的棱线选EM、MN、NF、FE分别为半径依次画弧截取水平线，在水平线上得交点为M、N、F和E点。在M点至N点和F点至E点的两段线段上，把每段线段四等分，在M点至N点线段上的等分点是4′、3′、2′点，在F点至E点线段上的等分点是2、3、4点。过水平线上的各点向上做垂直于水平线的垂线。量取各点的上垂线长，得交点为E、M、4′、3′、2′、N、F、2、3、4、E点，其中：E点的上垂线长等于主视图中方管棱线端点E（F）至延长线上相贯点E的长；M点的上垂线长等于主视图中方管棱线端点M（N）至延长线上相贯点M的长；N点的上垂线长等于主视图中方管棱线端点M（N）至延长线上相贯点N的长；F点的上垂线长等于主视图中方管棱线端点E（F）至延长线上相贯点F的长；各等分点4′、3′、2′点和2、3、4点的上垂线长分别对应主视图中方管棱线端点至各相贯点的长。分别用线段连接上垂线上的交点E点至M点和N点至F点，再分别用曲线圆滑连接上垂线上的交点M、4′、3′、2′、N点和F、2、3、4、E点，连接后的图形即为方管的展开图。

圆锥管的展开：把分解后的圆锥管视图移到一个适宜位置以待展开，照录锥底两端点A、B点和锥顶O点，并在锥底线段AB上做锥底的半圆。从主视图中看到相贯线线段FE、EM、MN都不在一条素线上，从前述“相贯线的性质与特点”中得知，圆锥管上相贯线线段为直线且不在同一条素线上时，相贯线在做展开线时为曲线。为使相贯线段FE、EM、MN展开曲线时做得准确，有必要对圆锥管主视图中的各段相贯线段进行约等分。约等分的方法是将最长相贯线线段EM进行四等分，再把最短相贯线线段NM进行两等分，在相贯线线段NM上得等分点为1′点和2′点（即M点），在相贯线线段EM上得等分点为2′点（即M点）、3′点、4′点、5′点、6′点（即E点）。

从锥顶O点引素线分别过两段相贯线线段上的各等分点，交于锥底线段AB上，在锥底线段AB上得交点为1、2、3、4、5、6点。从锥顶O点所引下的六条素线过相贯线线段FE，在FE上得交点为1、2、3、4、5、6点（即E点）。过相贯线线段上的各点做平行线平行于锥底线段AB，交于边线OB上，则锥顶O点至边线OB上各点的长即是锥顶O点至各相贯点的素线实长。

过锥底线段AB上的交点（即1、2、3、4、5、6点）向下做垂线垂直于锥底线段AB，交于锥底线段AB所做的半圆周线上，得交点为1、2、3、4、5、6点。半圆周线上的这些交点即是各段相贯线线段约等分点素线交于锥底圆周线上的实际位置点。以锥顶O点为圆心，O点至锥底端点B的长为半径画弧，在弧线上任选一点为B点，以这个B点为起点，锥底半圆六等分中的一份弧长为半径依次截取弧线十二次，得终点B。过弧线上两个B点做线段与锥顶O点相连。在两个B点间的弧线中点做一A点，以这个A点为圆心，锥底半圆周线上、、、、、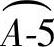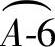的弧长为半径分别画弧，交在两上B点间的圆弧线上，得交点依次为A、1、2、3、4、5、6点。过这些交点做线段分别与锥顶O点相连。以锥顶O点为圆心，锥顶O点至圆锥管边线OB上各自相贯点素线实长为半径分别画弧，各弧线与锥顶相连的各线段分别对应相交，得交点为F、1、2、3、4、5、6（即E点）、5′、4′、3′、2′（即M点）、1′、N点。F点至N点因为在同一条素线上，所以用线段相连，其余交点用曲线圆滑连接，连接后的图形即是圆锥管开孔的展开，整个扇形图即是圆锥管开孔的展开图。